운동량 보존의 법칙, 선운동량보존법칙 ¶
운동량보존법칙(law of momentum conservation, law of conservation of momentum) or 운동량보존,momentum_conservation
외력을 받지 않는 계 내부에서 전체 운동량의 합이 보존된다는 법칙
외력을 받지 않는 계 내부에서 전체 운동량의 합이 보존된다는 법칙
선운동량이 보존되는 이유는 공간이 균질하기 때문이다.
뇌터의 정리에 의하면, 대칭성이 있으면 그에 상응하는 보존량이 있는데,
- 공간이 균질하다는 대칭성에 상응하는 보존량: 선운동량
- 공간이 등방성이라는 대칭성에 상응하는 보존량: 각운동량
Noether's Theorem
....
보존,conservation law ⇔ 대칭성,symmetry
운동량,momentum ⇔ translation in 공간,space
에너지,energy ⇔ translation in 시간,time
그 외에운동량,momentum ⇔ translation in 공간,space
에너지,energy ⇔ translation in 시간,time
- 시간변환에 대한 대칭성에 대응되는 보존량: 에너지,energy
| 자연의 대칭성 | 상응하는 보존량 |
| 공간의 균질성 | 선운동량 |
| 공간의 등방성 | 각운동량 |
| 시간변환의 대칭성 | 에너지 |
....
외부에서 힘이 작용하지 않으면 충돌/폭발 등에서 운동량이 보존된다. (운동량보존법칙)
외부에서 토크가 작용하지 않으면 물체의 각운동량은 보존된다는 이 자연의 법칙을 각운동량 보존 법칙(law of angular momentum conservation)이라고 한다.
직선상에서 속도 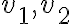 로 운동하던 질량
로 운동하던 질량 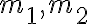 인 두 물체 A, B가 정면 충돌하여 속도가 각각
인 두 물체 A, B가 정면 충돌하여 속도가 각각 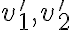 으로 되었다. 충돌하는 동안 물체 B가 A로부터 받은 평균 힘을
으로 되었다. 충돌하는 동안 물체 B가 A로부터 받은 평균 힘을 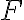 라고 하면, 작용-반작용 법칙에 의해 물체 A는 B로부터
라고 하면, 작용-반작용 법칙에 의해 물체 A는 B로부터 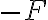 의 힘을 받는다.
의 힘을 받는다.
두 물체 A, B가 접촉한 시간을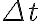 라고 할 때, 물체 A와 B가 받은 충격량,impulse은 각각
라고 할 때, 물체 A와 B가 받은 충격량,impulse은 각각
이 두 식을 더하여 정리하면,
이와 같이 일반적으로 외력이 작용하지 않으면 물체들의 총 운동량은 항상 일정하게 보존된다. (운동량 보존의 법칙)
두 물체 A, B가 접촉한 시간을
| A가 받는 충격량 | |
| B가 받는 충격량 |
식의 좌변은 충돌 전 운동량의 합을, 우변은 충돌 후 운동량의 합을 나타낸다.
이와 같이 일반적으로 외력이 작용하지 않으면 물체들의 총 운동량은 항상 일정하게 보존된다. (운동량 보존의 법칙)
(물리I 지학사)
선운동량의 보존법칙과,
운동량의 시간에 대한 변화율이 힘이라는 사실과의 관계
운동량의 시간에 대한 변화율이 힘이라는 사실과의 관계
게다가
질량이 변하지 않으면
따라서 힘이 0이면 속도변화가 0임.
외부 힘이 0이면 선운동량이 보존
외부 토크가 0이면 각운동량이 보존
외부 토크가 0이면 각운동량이 보존

