운동량,momentum 특히 선운동량,linear_momentum의 변화량.
또는 I=FΔt에서 N·s
I = Δp = m v2 - m v1
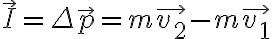
따라서 단위는 운동량과 같음. kg m s-1또는 I=FΔt에서 N·s
q: 각운동량의 변화인 각충격량 angular impulse 같은것도 있는지..
운동량에 영향을 주는 물리량.
물체가 받은 충격량은 그 물체의 운동량의 변화량과 같다.
힘이 일정할 때,
작용한 힘 × 작용한 시간.
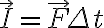
따라서 단위: N·s
작용한 힘 × 작용한 시간.
힘이 일정하지 않다면?
사실 일반적으로, 충격량은 힘,force을 시간,time에 따라 적분한 것. 충격량만큼 입자의 운동량,momentum이 변함. 시각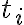 에서부터
에서부터 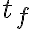 까지 동안 물체가 받은 충격량은
까지 동안 물체가 받은 충격량은
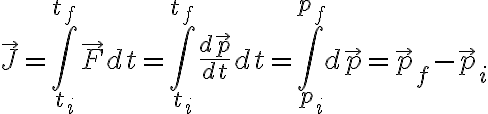
운동량보존법칙과 관련. curr see 보존,conservation
사실 일반적으로, 충격량은 힘,force을 시간,time에 따라 적분한 것. 충격량만큼 입자의 운동량,momentum이 변함. 시각
중고등학교 설명 ¶
알짜힘은 운동량의 시간에 대한 변화율
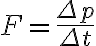
따라서
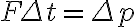
이 때 좌변을 충격량이라고 하고, 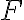 를 충격력이라고 한다.
를 충격력이라고 한다.
즉 운동량의 변화는 충격량과 같다.
즉 운동량의 변화는 충격량과 같다.
충격량 = 충격력(작용한 힘) × 힘을 작용한 시간
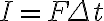
이 식을 계속 쓰면 (힘은 일정)
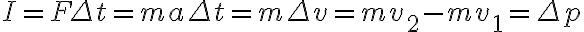
즉, 충격량은 물체의 운동량의 변화량과 같다.
또한, 물체의 질량이 변하지 않는 경우에는
}{\Delta t}=m\frac{\Delta v}{\Delta t}=ma)
(뉴턴의 운동 2법칙)
즉, 충격량은 물체의 운동량의 변화량과 같다.
또한, 물체의 질량이 변하지 않는 경우에는
(뉴턴의 운동 2법칙)
7차 고등학교 물리I 청문각 p51 ¶
직선 상에서 속도 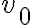 로 운동하고 있는 질량
로 운동하고 있는 질량 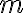 인 실험용 수레를 일정한 힘
인 실험용 수레를 일정한 힘 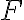 로 시간
로 시간 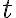 동안 밀어서 속도
동안 밀어서 속도 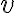 가 되었다면, 가속도
가 되었다면, 가속도  는
는
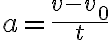
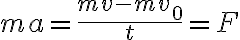
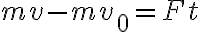
운동량 변화의 원인은 (작용한)힘 곱하기 (작용한)시간이며 이것을 충격량이라 한다.
운동량의 변화량은 충격량과 같다.
운동량의 변화량은 충격량과 같다.
7차 고등학교 물리I 중앙교육 p58 ¶
일정한 속도 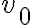 로 운동하는 질량
로 운동하는 질량 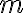 인 물체에 짧은 시간 간격
인 물체에 짧은 시간 간격 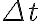 동안 일정한 힘
동안 일정한 힘 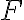 가 작용하여 속도가
가 작용하여 속도가 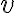 로 되었다면,
로 되었다면,
힘이 작용하는 시간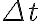 동안 물체에 생긴 가속도는
동안 물체에 생긴 가속도는
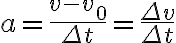
이다. 따라서 뉴턴 운동 법칙에 의해
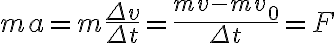
다시 쓰면
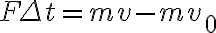
여기서 좌변은 충격량이고 우변은 운동량의 변화.
i.e.
물체에 주어진 충격량은 물체에 일어난 운동량의 변화와 같다.
힘이 작용하는 시간
i.e.
물체에 주어진 충격량은 물체에 일어난 운동량의 변화와 같다.
충격량은 크기와 방향이 있으며 (벡터량) 방향은 힘의 방향과 같고 단위는 N s (kg m / s)
충격이 가해지는 동안의 평균 힘 = 충격력. 이것은 위 식에서 F인

에 해당.
힘,force, 즉 충격력과의 관계 ¶
힘이 일정하다면, 곱셈으로 계산.
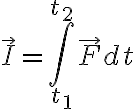
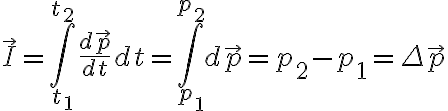
I = F Δt
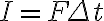
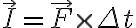
충격량 = 충격력 × 시간
힘이 변한다면, 적분으로 계산.충격량 = 충격력 × 시간
단어 impulse를 공유하는
임펄스함수,impulse_function
단위임펄스함수,unit_impulse_function
.. 임펄스,impulse 페이지 만들어도 무방할듯
{
impulse_train = sampling_function = Dirac_comb .... Dirac_comb
Dirac_comb
}
임펄스함수,impulse_function
단위임펄스함수,unit_impulse_function
.. 임펄스,impulse 페이지 만들어도 무방할듯
{
impulse_train = sampling_function = Dirac_comb ....
}
Up:
Misc:
Misc:
충격량을 한국에서는 I로, 영어권에선 J로 표기하는 듯. I는 관성모멘트,moment_of_inertia에 쓰이기 때문에 J를 쓰는 듯.
회전운동의 경우 angular impulse(ΔL)이란 것도 존재한다.
알파벳 I는 관성모멘트,moment_of_inertia도 사용함.
회전운동의 경우 angular impulse(ΔL)이란 것도 존재한다.
알파벳 I는 관성모멘트,moment_of_inertia도 사용함.


![[http]](/123/imgs/http.png)
![[https]](/123/imgs/https.png)