1의 거듭제곱근 - root of unity : 거듭제곱하여 1이 되는 복소수
1의 n제곱근 - nth root of unity : n제곱하면 1이 되는 복소수
보통 한 식에 n개씩 나오므로 복수형을 써서 roots of unity로 자주 언급됨
1의 n제곱근 - nth root of unity : n제곱하면 1이 되는 복소수
보통 한 식에 n개씩 나오므로 복수형을 써서 roots of unity로 자주 언급됨
지수를 양의 정수로 거듭제곱,멱,power하여 (i.e. 같은 것을 양의 정수 번 곱하여) 1이 되는 복소수,complex_number.
Any complex number that yields 1 when raised to some positive integer power n.
Any complex number that yields 1 when raised to some positive integer power n.
이 근,루트,root/해,solution들은 단위원,unit_circle 위에 ) 을 기준으로
을 기준으로  개가 동일 간격으로 배열된 점....? 즉 그 각,angle은
개가 동일 간격으로 배열된 점....? 즉 그 각,angle은 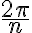 의 정수배, 즉 저거 곱하기 {0,1,...,n-1} ... ... chk
의 정수배, 즉 저거 곱하기 {0,1,...,n-1} ... ... chk
(비교:
(비교:
복소평면,complex_plane위에서,
1의 거듭제곱근들은 단위원,unit_circle 위의 점들,
(어떤 수)의 거듭제곱근,nth_root들은 중심이 원점,origin인 원,circle 위의 점들,
다항식이 좀 복잡해지면 or 더이상 원 모양이 아니고 어떤 곡선모양...? 리마송 같은 모양도 있고....tbw
) - chk1의 거듭제곱근들은 단위원,unit_circle 위의 점들,
(어떤 수)의 거듭제곱근,nth_root들은 중심이 원점,origin인 원,circle 위의 점들,
다항식이 좀 복잡해지면 or 더이상 원 모양이 아니고 어떤 곡선모양...? 리마송 같은 모양도 있고....tbw
식
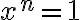
을 만족하는 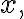 즉 1의 n제곱근은 n개이며 그 꼴은
즉 1의 n제곱근은 n개이며 그 꼴은
)
여기서
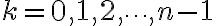
기호는  개 중
개 중  번째를 다음과 같이 표기:
번째를 다음과 같이 표기:
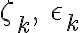
A complex number  is called an n-th root of unity, if
is called an n-th root of unity, if
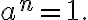
)
각 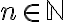 에 대해, 다음과 같은, 서로 다른, 정확히 n개의, n-th roots of unity
에 대해, 다음과 같은, 서로 다른, 정확히 n개의, n-th roots of unity
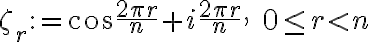
가 있다.
최성우 ¶
따라서
ex.
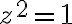

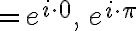
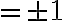
ex.

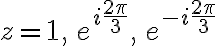
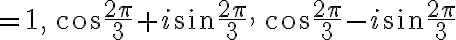
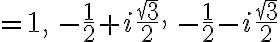
(참고로 이하 일반적인 수의 n승근)
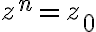 의 해 (z0: 정해진 복소수)
의 해 (z0: 정해진 복소수)
150°에서
270°에서
Twins:
 1의_거듭제곱근
1의_거듭제곱근
 Root_of_unity (occasionally called a de Moivre number)
Root_of_unity (occasionally called a de Moivre number)
https://mathworld.wolfram.com/RootofUnity.html
https://proofwiki.org/wiki/Definition:Root_of_Unity
https://everything2.com/title/nth roots of unity
https://artofproblemsolving.com/wiki/index.php/Roots_of_unity
https://mathworld.wolfram.com/RootofUnity.html
https://proofwiki.org/wiki/Definition:Root_of_Unity
https://everything2.com/title/nth roots of unity
https://artofproblemsolving.com/wiki/index.php/Roots_of_unity
기타 관련된 몇가지 단어들 (내용 짧음)
https://mathworld.wolfram.com/deMoivreNumber.html
https://mathworld.wolfram.com/CyclotomicEquation.html { cyclotomic .. 그리고 이름 비슷한 cyclotomic_polynomial => https://everything2.com/title/cyclotomic polynomial }
cyclotomic .. 그리고 이름 비슷한 cyclotomic_polynomial => https://everything2.com/title/cyclotomic polynomial }
https://mathworld.wolfram.com/PrimitiveRootofUnity.html
https://mathworld.wolfram.com/deMoivreNumber.html
https://mathworld.wolfram.com/CyclotomicEquation.html {
https://mathworld.wolfram.com/PrimitiveRootofUnity.html
primitive_root_of_unity
이건 원시근,primitive_root and 일의거듭제곱근,unity_root? chk.
최선의 번역은?
 Primitive.Root.of.Unity
Primitive.Root.of.Unity
https://mathworld.wolfram.com/PrincipalRootofUnity.html이건 원시근,primitive_root and 일의거듭제곱근,unity_root? chk.
최선의 번역은?
관련 related
제곱근,square_root - n=2이고 우변이 1이 아닐 수도 있는 경우. chk
거듭제곱근,nth_root - n=(정수? 자연수?...TBW)이고 우변이 1이 아닐 수도 있는, 즉 더 일반적인 경우. chk
약간 관련:거듭제곱근,nth_root - n=(정수? 자연수?...TBW)이고 우변이 1이 아닐 수도 있는, 즉 더 일반적인 경우. chk
공통: nth_root_of_unity ... https://everything2.com/title/nth roots of unity https://everything2.com/title/n nth complex roots of unity
드무아브르_공식,de_Moivre_s_formulaUp:
근,루트,root or 거듭제곱근,nth_root curr goto 제곱근,square_root
복소근 complex_roots
복소수,complex_number
복소해석,complex_analysis
복소근 complex_roots
복소수,complex_number
복소해석,complex_analysis

