Difference between r1.26 and the current
@@ -20,7 +20,7 @@
$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$ (Bayes' rule의 가장 간단한 경우)에 $A=A_i$ 를 적용하면 다음을 얻을 수 있다.
$P(A_i|B)=\frac{P(B|A_i)P(A_i)}{\sum_{i=1}^{n}P(B|A_i)P(A_i)}$
이것을 [[베이즈_정리,Bayes_s_theorem]]라고 한다.
이것을 [[베이즈_정리,Bayes_theorem]]라고 한다.
(Schaum Prob, RV, and RP)
@@ -61,14 +61,14 @@
$=P(A|B_1)P(B_1)+P(A|B_2)P(B_2)+\cdots+P(A|B_n)P(B_n)$$=\sum_{i=1}^{n}P(A|B_i)P(B_i)$
이 사실은 [[베이즈_정리,Bayes_s_theorem]]에 쓰인다.
이 사실은 [[베이즈_정리,Bayes_theorem]]에 쓰인다.
(Leon-Garcia p.63)
----
[[분할,partition]]의 정의와 [[조건부확률,conditional_probability]]의 정의로부터 '''전확률 정리'''를 이끌어 낸다.
(유도과정은 분할 페이지에도 있음.)
'''전확률정리'''로부터 [[베이즈_정리,Bayes_s_theorem]]를 이끌어낸다.
'''전확률정리'''로부터 [[베이즈_정리,Bayes_theorem]]를 이끌어낸다.
@@ -124,7 +124,7 @@
관련:
[[베이즈_정리,Bayes_s_theorem]]
[[베이즈_정리,Bayes_theorem]]
[[확률,probability]][[조건부확률,conditional_probability]]
@@ -135,5 +135,4 @@
[[https://terms.naver.com/entry.naver?docId=3338097&cid=47324&categoryId=47324 수학백과: 전체 확률의 법칙]]Up: [[확률,probability]]
AKA 전체 확률에 대한 정리(theorem on total probability), 전체확률법칙(law of total probability), 전확률공식(total probability formula)
1. 설명 ¶
표본공간  의 분할
의 분할 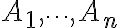 이 있을 때, 사건
이 있을 때, 사건 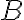 의 확률을 구하는 방법.
의 확률을 구하는 방법.
=)
) ...바로 교집합의 확률을 더하는 것이다.
...바로 교집합의 확률을 더하는 것이다.
P(A_i))
의의: unconditional probability ![$P[B]$ $P[B]$](/123/cgi-bin/mimetex.cgi?\Large P[B]) 를, weighted conditional probabilities(조건부확률,conditional_probability)의 합
를, weighted conditional probabilities(조건부확률,conditional_probability)의 합 ) 으로 구할 수 있다.
으로 구할 수 있다.
- 분할로 이루어진
개의 사건
이 있다. (mutually exclusive and exhaustive)
- 어떤 사건
가 있다.
(Schaum Prob, RV, and RP)
3. 설명 계속 ¶
P(B)
= P(B∩A1) + P(B∩A2) + ... + P(B∩An)
= P(A1) P(B|A1) + P(A2) P(B|A2) + ... + P(An) P(B|An)
= P(B∩A1) + P(B∩A2) + ... + P(B∩An)
= P(A1) P(B|A1) + P(A2) P(B|A2) + ... + P(An) P(B|An)
표본공간,sample_space  가 상호 배반인
가 상호 배반인 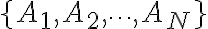 사건의 합으로 표현할 수 있다 가정한다. 즉
사건의 합으로 표현할 수 있다 가정한다. 즉

그러면 어떤 사건,event 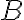 는 다음과 같이 표현할 수 있다.
는 다음과 같이 표현할 수 있다.
)
사건 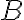 의 확률은 상호 배반이니까 단순히 더하기만 하면 되므로
의 확률은 상호 배반이니까 단순히 더하기만 하면 되므로
=\sum_{n=1}^{N}P(B\cap A_n)=\sum_{n=1}^{N}P(A_n)P(B|A_n))
from http://contents.kocw.or.kr/document/lec/2012/Hufs/KimMyoungJin/05.pdf p10
표본공간,sample_space S의 분할,partition
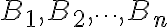 이 있을 때,
이 있을 때,
어떤 사건,event A는 서로 배반인 사건의 합집합으로 나타낼 수 있다.
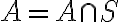
)
\cup(A\cap B_2)\cup\cdots\cup(A\cap B_n))
따라서 A의 확률,probability은,
=P(A\cap B_1)+P(A\cap B_2)+\cdots+P(A\cap B_n))
P(A|B_1)+P(B_2)P(A|B_2)+\cdots+P(B_n)P(A|B_n))
P(B_1)+P(A|B_2)P(B_2)+\cdots+P(A|B_n)P(B_n))
P(B_i))
이 사실은 베이즈_정리,Bayes_theorem에 쓰인다.
(Leon-Garcia p.63)
전확률정리로부터 베이즈_정리,Bayes_theorem를 이끌어낸다.
5. Example ¶
Q: 1~10에서 두 숫자를 뽑는다. without replacement. 두번째 숫자가 5일 확률?
Sol.
A1 : 첫번째에 1을 뽑는 사건
A2 : 첫번째에 2를 쁩는 사건
...
A10 : 첫번째에 10을 뽑는 사건
B : 두번째에 5를 뽑는 사건
P(B)?
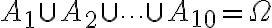
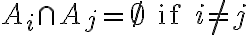
Sol.
A1 : 첫번째에 1을 뽑는 사건
A2 : 첫번째에 2를 쁩는 사건
...
A10 : 첫번째에 10을 뽑는 사건
B : 두번째에 5를 뽑는 사건
P(B)?
...
6. Example 2 ¶
생산품 50%를 A라인, 30%를 B라인, 20%를 C라인에서 만들고,
각각 3% 5% 6%의 불량품이 생김.
임의로 선택한 제품이 불량품일 확률은?
각각 3% 5% 6%의 불량품이 생김.
임의로 선택한 제품이 불량품일 확률은?
임의로 하나의 제품을 선택했을 때 A라인에서 생산되었을 사건을 A,
마찬가지로 B, C 정의하고, 불량품일 사건을 D라 하면
P(D) = P(A∩D) + P(B∩D) + P(C∩D)
마찬가지로 B, C 정의하고, 불량품일 사건을 D라 하면
P(D) = P(A∩D) + P(B∩D) + P(C∩D)
= P(A)·P(D|A) + P(B)·P(D|B) + P(C)·P(D|C)
= 0.5 × 0.03 + 0.3 × 0.05 + 0.2 × 0.06 = 0.042
from http://blog.naver.com/mykepzzang/220834919339= 0.5 × 0.03 + 0.3 × 0.05 + 0.2 × 0.06 = 0.042
Up: 확률,probability


![[https]](/123/imgs/https.png)