앙페르_법칙,Ampere_s_law

Ampère's circuital law
AKA 암페어 법칙, 오른나사 법칙


전류가 흐르는 도선이 있다면, 주위에 자기장이 생김
그 자기장(B)은 전류(I)에 비례, 거리(r)에 반비례

$B\propto\frac{I}{r}$
$B=k\frac{I}{r}$
$B=\frac{\mu_0}{2\pi}\frac{I}{r}$

TODO MKL Ampere-Maxwell

$\oint_C \vec{B}\cdot d\vec{x} = \mu_0 i$
(Y15C)

CHK
{
반지름이 r인 원 둘레를 따라 적분 (폐곡면을 따라 선적분,line_integral)하면
$\oint\vec{B}\cdot d\vec{s}=\oint \frac{\mu_0 I}{2\pi r}\cdot 2\pi r=\mu_0 I$

자기장과 폐곡면 내부 전류와의 관계.

src: [http]황종승 자기장의 원천(2)
}
CHK {
$B=(2\times 10^{-7}\,\mathrm{N/A}^2)\times\frac{I}{r}$ - 직선 도선
$B=(2\pi\times 10^{-7}\,\mathrm{N/A}^2)\times\frac{I}{r}$ - 원형 도선
$B=(4\pi\times 10^{-7}\,\mathrm{N/A}^2)\times nI$ - 솔레노이드
}
$\oint_{C}\vec{B}\cdot d\vec{s}=\mu_0 I=\mu_0\int_{S}\vec{J}\cdot d\vec{S}$
면적분,surface_integral의 범위 S는 선적분,line_integral의 범위인 폐곡선,closed_curve C가 둘러싼 넓이
무한도선(무한히 긴 직선 도선)에서 거리 r 떨어진 곳의 자기장의 크기
$B(r)=\frac{\mu_0I}{2\pi r}$
$\sum |\vec{B}| |\Delta s| \cos\theta = \mu_0 I$

$\sum B_{||} \Delta \ell = \mu_0 I$
where
$B_{||}$ : $\vec{B}$ 의 $\Delta\ell$ 과 평행인 성분
$\vec{B}$ 는 원의 접선 방향 벡터임.

길고 곧은 전선에 전류 I가 흐른다면, B가
$B_{||}=B$
로 일정하고 원 둘레 길이는 $2\pi r$ 이므로
$\sum B_{||}\Delta\ell=B_{||}\sum\Delta\ell=B(2\pi r)=\mu_0I$
양변을 $2\pi r$ 로 나누면
$B=\frac{\mu_0 I}{2\pi r$

(Serway 9e p. 665)
전류 I0가 흐르는 전선 주위 거리 r에서 자속밀도,magnetic_flux_density B와 자기장세기,magnetic_field_intensity H는
B = μ0 I0 / (2πr)
H = I0 / (2πr)
[https]src: 두산백과 자기장의 세기

즉
H는 자기장이 있는 공간의 자기적 특성을 생각지 않은 양이고
B는 자기적 특성을 생각한 양


닫힌 경로(앙페르 경로)에서 자기장과 미소길이의 스칼라곱의 선적분은 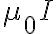$\mu_0 I$ 이다. I는 앙페르 경로에 둘러싸인 총 정상 전류를 뜻함.

$\oint\vec{B}\cdot d\vec{l} = \mu_0 I_{\text{encl}}$

  • $\mu_0 $ = 자유공간의 투자율 (permeability of free space) : 어떤 매질이 주어진 자기장에 의해 자기화,magnetization하는 정도 (See 투자율,permeability)
  • $I_{\text{encl}}$ : 앙페르 경로에 둘러싸인 전류의 총 합

[edit]

하이탑 물2의 서술

먼저 ∮는 닫힌경로,closed_path에 대해 적분한다는 뜻.

앙페르 법칙:
$\oint\vec{B}\cdot d\vec{\ell}=\mu_0I$

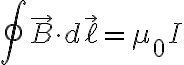
좌변 : (자기장 세기)·(미소 경로)
우변 μ0 : 진공 투자율(permeability constant, 4π×10-7 H/m)
우변 I : 닫힌 경로에 흐르는 전류의 세기

[edit]

물리실험프린트에서

Ampere의 법칙
$\oint_C \vec{B}\cdot d\vec{s}=\mu_0 I$
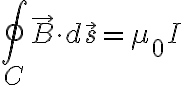
where
$\vec{B}$ : 자속밀도,magnetic_flux_density
μ0 : 진공의 투자율,permittivity,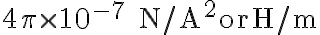 $4\pi\times 10^{-7}\;\mathrm{N/A^2 or H/m}$
I : 폐곡선 C로 둘러싸인 영역 S를 지나가는 전류,electric_current

Ampere-Maxwell의 법칙
전기장,electric_field에 의해 자기장,magnetic_field이 형성
$\oint_C \vec{B}\cdot d\vec{s}=\mu_0 I+\mu_0\epsilon_0\frac{d\Phi_E}{dt}$
where
$\Phi_E=\int_S\vec{E}\cdot d\vec{a}$ : 폐곡선 C로 둘러싸인 영역
$\epsilon_0\frac{d\Phi_E}{dt}$ : 변위전류,displacement_current, 직류일 땐 0



(Ampère's force law 와의 차이는??)

맥스웰_방정식,Maxwell_equation의 네번째 법칙은 앙페르-맥스웰 법칙.

[edit]

변위전류와 일반화된 암페어의 법칙

일단 다음 암페어 법칙을 이용해 전류가 흐르는 도체에서 자기장을 계산 가능.
$\oint\vec{B}\cdot d\vec{s}=\mu_0 I$
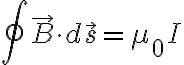
Maxwell은 이 식의 우변에
$I_d=\epsilon_0\frac{d\Phi_e}{dt}$
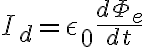
로 정의되는 변위전류,displacement_current라는 부가항을 가정하여 (어떤 모순, 생략) 문제를 해결했다.
이로서 암페어 법칙의 일반화된 형태(암페어-맥스웰의 법칙 Ampere-Maxwell Law)는
$\oint\vec{B}\cdot d\vec{s}=\mu_0(I+I_d)=\mu_0I+\mu_0\epsilon_0\frac{d\Phi_e}{dt}$