호의길이 , 호(의) 길이 (kms)
/// merge from 호,arc 의 부분 => 호,arc
TBW ¶
특별한 경우인 원호,circular_arc의 arclength는 쉬운 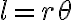
일반적인 경우인 parametric 곡선,curve의 arclength는 // parametric_curve
) 형태일 때
형태일 때
) 형태일 때
형태일 때
 \\ y=g(t) \end{cases}) 형태일 때
형태일 때
...tbw
일반적인 경우인 parametric 곡선,curve의 arclength는 // parametric_curve
...tbw
ds ¶
직각삼각형에서 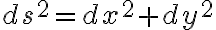
기호 )
곡선 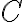 가 다음과 같은 벡터함수,vector_function이고,
가 다음과 같은 벡터함수,vector_function이고, 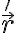 이 연속이며,
이 연속이며, 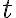 가
가  에서
에서 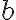 로 증가함에 따라
로 증가함에 따라 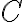 는 꼭 한번만 궤적을 이룬다고 하자.
는 꼭 한번만 궤적을 이룬다고 하자.
=f(t)\hat{i}+g(t)\hat{j}+h(t)\hat{k},\;\;a\le t \le b)
이 때 호의 길이함수(arc length function) 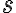 를 다음과 같이 정의한다.
를 다음과 같이 정의한다.
=\int_a^t \left| \vec{r}{}%27(u) \right| du = \int_a^t \sqrt{\left(\frac{dx}{du}\right)^2 + \left(\frac{dy}{du}\right)^2 + \left(\frac{dz}{du}\right)^2}du)
따라서 ) 는
는 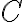 의
의 ) 와
와 ) 사이의 길이이다.
사이의 길이이다.
FTC 1을 이용해서 양변을 미분하면 다음을 얻는다.
 \right|)
(Stewart ch13.3 arc length and curvature)
FTC 1을 이용해서 양변을 미분하면 다음을 얻는다.
Bazett ¶
(1)
See next: 곡률,curvature의 Bazett 부분
tmp and mklink - curve_length (writing)
이건 경로,path의 길이도 ok인데... ....그런가? rationale/src?
길이,length 맨위에 어디어디서 언급되었는지 있으며 거기서 옮겨올것
https://www.mathsisfun.com/calculus/arc-length.html
https://tutorial.math.lamar.edu/classes/calcii/arclength.aspx
https://tutorial.math.lamar.edu/classes/calcii/arclength.aspx
// from wpen 대충.
일단, 문제를 간단히 해서 곡선 위 유한 개의 점으로 나눈 선분,line_segment들로 된 polygonal path( Polygonal_chain : connected series of line segments)의 총 길이를 생각.
Polygonal_chain : connected series of line segments)의 총 길이를 생각.
각 길이는 피타고라스_정리,Pythagorean_theorem로 구하여 합,sum하면 전체 길이.
이것은 많은 선분들을 사용한 근사,approximation.
참값을 구하려면 각 선분의 길이가 0으로 가는 극한,limit을.
(이상 chk)
일단, 문제를 간단히 해서 곡선 위 유한 개의 점으로 나눈 선분,line_segment들로 된 polygonal path(
각 길이는 피타고라스_정리,Pythagorean_theorem로 구하여 합,sum하면 전체 길이.
이것은 많은 선분들을 사용한 근사,approximation.
참값을 구하려면 각 선분의 길이가 0으로 가는 극한,limit을.
(이상 chk)
bmks ko ¶
곡선의 길이(Arc Length) https://suhak.tistory.com/313
곡선의 길이 https://mathphysics.tistory.com/57 (Stewart 7e)
곡선의 길이 https://mathphysics.tistory.com/57 (Stewart 7e)


![[https]](/123/imgs/https.png)