AKA LR 회로
그리고
R/L은 1/s,
L/R은 시간 단위(sec)를 가짐
R/L은 1/s,
L/R은 시간 단위(sec)를 가짐
I-t 그래프는 처음에 급격하게 증가하며 차차 완만하게 점근선 I=E/R까지 접근하는 모습.
시간이 L/R이 되면 (t=L/R) I는 0.632(E/R)에 도달함.
시간이 L/R이 되면 (t=L/R) I는 0.632(E/R)에 도달함.
스위치를 바꾸어 회로에 전원이(E가) 빠지고 R, L만 남게 되면 자기장이 energy source역할을 하게 되고, 자기장이 없어지는 것을 막기 위한(없어지는 것에 저항하는) 유도전류가 생김.
해당 식은, 위의 식에 E=0을 적용하면
I-t 그래프는 exponentially decrease? 처음 E/R에서부터 처음에는 급격히 나중에는 완만히 떨어져서 I=0으로 접근하는 그래프.
t=L/R일 때, e-1=0.367, I=0.367(E/R) 만큼으로 떨어짐
}
송종현 CHK
{
고리법칙으로 정량적으로 분석:
회로를 닫을 때
)
)
where 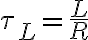 (시간상수,time_constant)
(시간상수,time_constant)
이 결과에 의해
)
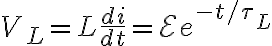
회로를 열 때

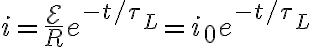
}
{
고리법칙으로 정량적으로 분석:
저항기는 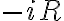
인덕터는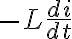
전지는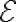
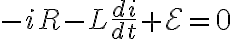
이 미방을 풀면(???)인덕터는
전지는
회로를 닫을 때
이 결과에 의해
수업에서.{
}
Halliday에서 {
전류의 감소 ¶
전지를 제거하면 저항에 흐르는 전류도 줄어드는데, 전류는 즉시 0이 되지 않는다. 이때의 미방은
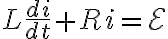
에 ℰ=0을 대입한 다음 식과 같다.
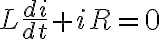
시간이 흐름에 따라 ... 전류는
=I_0e^{-t/\tau})
와 같이 감쇠한다. from Richardson 711; tocleanup
}
HRW p. 322 (30-6) ¶
저항 R, 유도용량 L, 단일고리 회로에 기전력 E가 걸리면, 전류는
) (전류 증가)
(전류 증가)
로 증가하며 τL은 회로의 유도시간상수
일정한 기전력을 없애면,
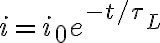 (전류 감소)
(전류 감소)
일정한 기전력을 없애면,
Zbar p. 403 ¶
직렬 RL회로의 임피던스,impedance는 다음과 같다.
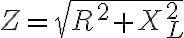
R이 일정하다면 XL에 따라 임피던스가 변화한다. 유도성리액턴스,inductive_reactance는,
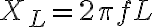
이므로 주파수가 일정하면 L의 변화에 따라 XL이 변하며 L이 일정하면 주파수의 변화에 따라 XL이 변한다.


![[http]](/123/imgs/http.png)