AKA 유도계수, 유도용량
기호:
단위: H (henry)
단위 유도:
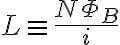
다시 말해
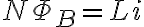
패러데이_법칙,Faraday_s_law와 위 식에 의해
마이너스 부호는 렌츠_법칙,Lenz_s_law
단위: H (henry)
단위 유도:
인덕턴스의 차원은 Φ/I = 자속/전류, 자속의 단위는 Wb = T·m2 이고 전류의 단위는 A, 따라서 인덕턴스의 단위는 Wb/A 또는 T·m2/A
NΦ=LI에서 Φ=BA이므로, NBA=LI, L=NBA/I, (B의 단위는 T, A의 단위는 m2, I의 단위는 A) 따라서 L의 단위는 T m2 A-1
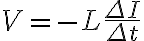 이므로
이므로 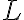 의 단위는
의 단위는 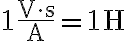
자속,magnetic_flux의 변화를 방해하는 작용의 세기NΦ=LI에서 Φ=BA이므로, NBA=LI, L=NBA/I, (B의 단위는 T, A의 단위는 m2, I의 단위는 A) 따라서 L의 단위는 T m2 A-1
- 자속이 (코일, 전선 등) 자신의 전류,electric_current에 의한 것일 때는 자체인덕턴스,self-inductance
- 자속이 외부(코일, 전선 등) 전류에 의한 것일 때는 상호인덕턴스,mutual_inductance
마이너스 부호는 렌츠_법칙,Lenz_s_law
회로의 빠른 전류 변화를 억제하는 역할을 함
그리하여 짧은 시간에 자주 변하는 고주파를 제거하는 high band pass filter에 쓰임
회로의 내부(폐곡면) 면적을 줄여서 인덕턴스를 낮출 수 있음
CHK
그리하여 짧은 시간에 자주 변하는 고주파를 제거하는 high band pass filter에 쓰임
회로의 내부(폐곡면) 면적을 줄여서 인덕턴스를 낮출 수 있음
CHK
코일의 인덕턴스(L)와 전류의 시간변화율은 유도전압을 결정
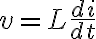
CHK
인덕턴스 L인 인덕터에 I의 전류가 흐르면 저장되는 에너지는
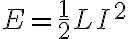
CHK
유도,induction에는 두 가지가 있다. 또 있나?
curr. see 전자기유도,electromagnetic_induction
자체유도,self-induction or 자체인덕턴스,self-inductance
상호유도,mutual_induction or 상호인덕턴스,mutual_inductance
curr. see 전자기유도,electromagnetic_induction
자체유도,self-induction or 자체인덕턴스,self-inductance
상호유도,mutual_induction or 상호인덕턴스,mutual_inductance
CHK
self inductance
![$\mathcal{E}=-L\frac{dI}{dt}=-N\frac{d\Phi}{dt}\;[{\rm V}]$ $\mathcal{E}=-L\frac{dI}{dt}=-N\frac{d\Phi}{dt}\;[{\rm V}]$](/123/cgi-bin/mimetex.cgi?\Large \mathcal{E}=-L\frac{dI}{dt}=-N\frac{d\Phi}{dt}\;[{\rm V}])
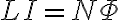
![$L=\frac{N\Phi}{I}\;[{\rm H}]$ $L=\frac{N\Phi}{I}\;[{\rm H}]$](/123/cgi-bin/mimetex.cgi?\Large L=\frac{N\Phi}{I}\;[{\rm H}])
mutual inductance
![$\mathcal{E}=-N\frac{d\Phi}{dt}=-M\frac{dI}{dt}\;[{\rm V}]$ $\mathcal{E}=-N\frac{d\Phi}{dt}=-M\frac{dI}{dt}\;[{\rm V}]$](/123/cgi-bin/mimetex.cgi?\Large \mathcal{E}=-N\frac{d\Phi}{dt}=-M\frac{dI}{dt}\;[{\rm V}])
유도: see also 전자기유도,electromagnetic_induction
3. from 황종승 ¶
L의 단위: H (henry)
코일에 전류가 흐르면 코일 속에 자기장이 생긴다. 전류를 변화시키면 코일을 통과하는 자속,magnetic_flux도 변하여 코일에 유도기전력,induced_emf이 나타난다. 렌츠의 법칙에 의해 유도기전력은 전류의 변화를 방해하는 방향으로 나타난다. 유도기전력의 크기는 전류의 시간변화율(dI/dt)에 비례한다.
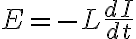
여기서
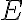 : 유도기전력
: 유도기전력
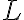 : 인덕턴스
: 인덕턴스


![[http]](/123/imgs/http.png)
![[https]](/123/imgs/https.png)