함수 ) 가
가 ![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) 에서 연속이고
에서 연속이고 ) 에서 미분가능할 때
에서 미분가능할 때
-f(a)}{b-a}=f^{\prime}(c))
인 ) 가 적어도 하나 존재한다.
가 적어도 하나 존재한다.
다시 말해 ),\;Q(b,f(b))) 에 대해
에 대해 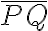 와 평행한 접선을
와 평행한 접선을 )\quad(a<c<b)) 에서 적어도 하나 그릴 수 있다.
에서 적어도 하나 그릴 수 있다.
1. Proof ¶
두 점 ),\;Q(b,f(b))) 를 지나는 직선을
를 지나는 직선을 ) 라 하면,
라 하면,
=\frac{f(b)-f(a)}{b-a}(x-a)+f(a))
이다. 이 때
=f(x)-g(x))
를 정의한다.
이때) 는
는 ![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) 에서 연속이고
에서 연속이고 ) 에서 미분가능하며
에서 미분가능하며 =h(b)=0) 이다.
이다.
이때
2. 코시의 평균값 정리, 일반화된 평균값 정리 ¶
MVT를 일반화시키면 코시의_정리가 된다.
두 함수  가 구간
가 구간 ![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) 에서 연속이고
에서 연속이고 ) 에서 미분가능하면
에서 미분가능하면
(g(b)-g(a))=g%27(c)(f(b)-f(a)))
를 만족하는 ) 가 존재한다.
가 존재한다.
코시의 평균값정리에서 =x,) 즉
즉 =1) 이면 일반 평균값정리가 된다.
이면 일반 평균값정리가 된다.
Suppose functions  and
and 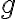 are continuous on
are continuous on ![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) and differentiable throughout
and differentiable throughout ) and also suppose
and also suppose \ne0) throughout
throughout .) Then
Then ) at which
at which
}{g%27(c)}=\frac{f(b)-f(a)}{g(b)-g(a)})
(Thomas)
(코시의 평균값 정리)
구간![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) 에서 연속이고, 구간
에서 연속이고, 구간 ) 에서 미분가능한 함수
에서 미분가능한 함수 ,g(x)) 에 대하여
에 대하여
-f(a)}{b-a}:\frac{g(b)-g(a)}{b-a} = f%27(c):g%27(c))
인 점 ) 가 존재한다.
가 존재한다.
구간
(김홍종 미적분학 1+ p110)
4. tmp (강우석 2021-03-10 1:11m) ¶
(Stewart 4.2 MVT, Example 2)
한 개를 보이려면? 존재성을 보여 0개가 아닌 1, 2, 3, ...개임을 보이고 유일성을 보여 2, 3, 4...개가 아닌 1개임을 보이면 됨.
② 유일성,uniqueness
롤_정리,Rolle_s_theorem 사용.
귀류법,proof_by_contradiction 사용.
=0) 이 두 근
이 두 근 ) 임을 가진다고 가정하면,
임을 가진다고 가정하면, =0,f(b)=0) 이다.
이다.  가 다항식이고 연속이고 미분가능하므로, Rolle 정리에 의해
가 다항식이고 연속이고 미분가능하므로, Rolle 정리에 의해
) s.t.
s.t. =0)
근데 =3c^2+1>0) 이다. 즉 0보다 항상 크다. 이것은 가정에 모순,contradiction.
이다. 즉 0보다 항상 크다. 이것은 가정에 모순,contradiction.
롤_정리,Rolle_s_theorem 사용.
귀류법,proof_by_contradiction 사용.
By ① and ②, ) has only one solution.
has only one solution.
6. tmp (강우석 2021-03-10 1:26m) ¶
// 미분이 0인 함수는 상수함수 뿐? Yes. 이유?
상수함수,constant_function의 미분이 0임을(i.e. 상수함수의 도함수가 영함수임을) 보이기는 쉽다. 한편 그 역인
미분이 0이 되는 함수는 상수함수? 그 외엔 없는지?
미분이 0이 되는 함수는 상수함수? 그 외엔 없는지?
Theorem: =0 \,\Rightarrow\, f) is constant
is constant
Proof
(일단 가 상수함수라는 것은,
가 상수함수라는 것은, 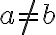 여도
여도 =f(b)) 라는 것.)
라는 것.)
Let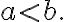
Applying MVT on,)
-f(a)}{b-a}=f%27(c)) for some
for some .)
그런데 =0) 이므로
이므로
-f(a)=0)
=f(a))
그래서 는 상수함수이다.
는 상수함수이다.
(일단
Let
Applying MVT on
그래서
// 미분이 양인 함수는 증가함수? Yes. 이유?
Theorem: >0 \,\Rightarrow\, f) is an increasing function
is an increasing function
Proof
(일단 가 증가함수라는 것은,
가 증가함수라는 것은, 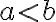 이면
이면 <f(b)) 라는 것.)
라는 것.)
Let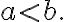
Applying MVT on,)
-f(a)}{b-a}=f%27(c)>0) for some
for some .)
-f(a)>0)
>f(a))
(일단
Let
Applying MVT on
// Cor. 미분이 같은 함수는 상수만큼 차이.
그리고 저 위 정리에서 나오는 따름정리는
미분이 같은 함수는 상수 차이가 난다는 것
미분이 같은 함수는 상수 차이가 난다는 것
Theorem
=g%27(x)\,\Rightarrow\,f(x)=g(x)+C)
Proof
도함수의 성질에 의해
-g(x)\right)%27=f%27(x)-g%27(x))
그리고 가정에서 이게 0과 같으므로
-g(x)\right)%27=f%27(x)-g%27(x)=0)
따라서 저 위 정리(도함수가 영함수인 함수는 상수함수)에 의해-g(x)) 가 상수함수이므로
가 상수함수이므로
-g(x)=C)
도함수의 성질에 의해
그리고 가정에서 이게 0과 같으므로
따라서 저 위 정리(도함수가 영함수인 함수는 상수함수)에 의해
응용질문.
Find all function) whose derivative is
whose derivative is 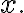
일단 꼴일 것 같다. 그런데 이것뿐이고 다른 형태가 없음을 증명하려면 위의 정리가 필요하다.
꼴일 것 같다. 그런데 이것뿐이고 다른 형태가 없음을 증명하려면 위의 정리가 필요하다.
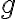 를 미분했더니
를 미분했더니 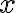 라고 해보자.
라고 해보자.
=x)
그리고
%27=x)
이다. 위 정리에 의해서
=\frac12x^2+C)
(이런 이유로 인해)
부정적분,indefinite_integral을 할 때 적분상수,integration_constant를 붙이는 것(으로 충분하다는 것)도 MVT에서 나오는 것이다.
Find all function
일단
부정적분,indefinite_integral을 할 때 적분상수,integration_constant를 붙이는 것(으로 충분하다는 것)도 MVT에서 나오는 것이다.
ex 38.
=\frac{\pi}{2}) 을 증명하라
을 증명하라
sol.
\right)%27)
^2})

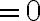
따라서 이건 상수함수이다.
=C)
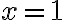 을 넣으면
을 넣으면 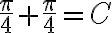
sol.
따라서 이건 상수함수이다.
7. tmp (단대 김도형) ¶
적분의 평균값 정리
![$f:[a,b]$ $f:[a,b]$](/123/cgi-bin/mimetex.cgi?\Large f:[a,b]) 에서 연속
에서 연속
![$\Rightarrow\;\exists c\in[a,b]$ $\Rightarrow\;\exists c\in[a,b]$](/123/cgi-bin/mimetex.cgi?\Large \Rightarrow\;\exists c\in[a,b]) such that
such that
=\frac1{b-a}\int_a^b f(x)dx)
pf.1.
최대최소정리,extreme_value_theorem,EVT에 의해
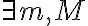 such that
such that ![$m\le f(x)\le M,\;\forall x\in[a,b]$ $m\le f(x)\le M,\;\forall x\in[a,b]$](/123/cgi-bin/mimetex.cgi?\Large m\le f(x)\le M,\;\forall x\in[a,b])
\le \int_a^bf(x)dx \le M(b-a))
dx \le M)
중간값정리,사이값정리,intermediate_value_theorem,IVT에 의해
![$\exists c\in[a,b]$ $\exists c\in[a,b]$](/123/cgi-bin/mimetex.cgi?\Large \exists c\in[a,b]) such that
such that =\frac1{b-a}\int_a^bf(x)dx)
최대최소정리,extreme_value_theorem,EVT에 의해
중간값정리,사이값정리,intermediate_value_theorem,IVT에 의해
pf.2.
=\int_a^x f(t)dt,\; a\le x\le b)
미분의 평균값정리에 의해
) such that
such that -F(a)}{b-a}=F%27(c)=f(c))
dt=f(x))
미분의 평균값정리에 의해
8. tmp; Weighted Mean Value Theorem for Integrals ¶
![[https]](/123/imgs/https.png) from stewartcalculus additional material file, p3
from stewartcalculus additional material file, p3

