1×1 행렬에서는 ![$A=[a]$ $A=[a]$](/123/cgi-bin/mimetex.cgi?\Large A=[a]) 일 때
일 때 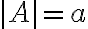
2×2 행렬에서
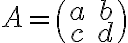 이면 그 행렬식은
이면 그 행렬식은 =\begin{vmatrix} a&b\\c&d \end{vmatrix}=ad-bc)
3×3 행렬에서
......TBW 여러 방법이 있는데,
사루스_규칙? Sarrus_rule (writing) { Rule_of_Sarrus ...
Rule_of_Sarrus ...  sarrus rule } <- 3x3에서만.
sarrus rule } <- 3x3에서만.
cofactor_expansion = Laplace_expansion (curr goto 여인수,cofactor) (is an 전개,expansion)
and?
(TODO '행렬식 구하는 법'을 별도의 문단으로 mk)
......TBW 여러 방법이 있는데,
사루스_규칙? Sarrus_rule (writing) {
cofactor_expansion = Laplace_expansion (curr goto 여인수,cofactor) (is an 전개,expansion)
and?
(TODO '행렬식 구하는 법'을 별도의 문단으로 mk)
표기
Sub:
Sub:
특성행렬식(characteristic determinant) characteristic_determinant - 별거 아니고 det(A-λI). 특성다항식,characteristic_polynomial과 마찬가지? 이걸 0으로 놓으면 특성방정식,characteristic_equation. (via: 고유값,eigenvalue의 앞부분 Kreyszig 인용)
resultant
resultant
1. 나눌 것 ¶
어떤 행렬 A의 행렬식 값
가역행렬,invertible_matrix은 행렬식이 0이 아니다.
det(A)=0 : ∄A−1 : A는 역행렬을 갖지 않는다.
det(A)≠0 : ∃A−1 : A의 역행렬이 존재한다.
i.e.det(A)≠0 : ∃A−1 : A의 역행렬이 존재한다.
가역행렬,invertible_matrix은 행렬식이 0이 아니다.
기하적으로는,
(대충) ~가(벡터,vectors들?) (서로 종속이 아니고 독립이어서) 넓이,area 부피,volume (.... 일반적으로 hypervolume?) 을 만들 수 있는지 '결정하는가'(hence the name)를 알려주는?
2차정사각행렬의 행렬식의 절대값은 두 벡터로 이루어진 평행사변형의 넓이,area, // 참고: (proof without words) determinant = area? https://lazymatlab.tistory.com/173
3차정사각행렬의 행렬식의 절대값은 세 벡터로 이루어진 평행육면체의 부피,volume CHK
3차정사각행렬의 행렬식의 절대값은 세 벡터로 이루어진 평행육면체의 부피,volume CHK
선형변환,linear_transformation의 스케일(scale) 성분을 나타낸다.
det의 부호에 따라
det의 부호에 따라
양이면 도형의 방향(orientation)이 보존되고,
음이면 도형의 방향이 보존되지 않는다.
[1]음이면 도형의 방향이 보존되지 않는다.
행렬에 의한 선형변환에 따른 면적 혹은 체적 변화율을 알아내고자 행렬식을 쓸 수 있다.
판별식,discriminant과 관계는?
(행렬식을 구하는 방법 중 하나)
어떤 구조에서 특징을 나타내는 실수 하나를 이끌어내본다 뭐 그런 아이디어는 비슷한 듯 한데
라플라스_전개,Laplace_expansion = 여인수 전개로 구할 수 있음. see 여인수,cofactor#s-2(행렬식을 구하는 방법 중 하나)
2. 성질 // from KUIAI, CHK ¶
기본연산과 행렬식
- A의 두 행(열)을 교환한 행렬이 B:
- A의 한 행(열)에 스칼라 c를 곱한 행렬이 B:
- 행렬의 스칼라 곱:
- A의 k번째 행(열)의 상수배를 j번째 행(열)에 더한 행렬이 B:
- A의 두 행(열)이 비례할 경우:
- 삼각행렬,triangular_matrix 및 대각행렬,diagonal_matrix의 행렬식:
주대각선 성분의 곱
- 항등행렬,identity_matrix의 행렬식:
- 전치,transpose 연산:
- det(AB)=det(A)det(B)
- A가 가역행렬,invertible_matrix이면
이고,
이유는 간단.이므로
- A가 비가역행렬이면
3. tmp links ko ¶
행렬식의 성질 및 행렬의 동등정리(equivalent theorem): equivalence thm 아닌가?
http://blog.naver.com/mykepzzang/221121796109
(가역성(related: 가역행렬,invertible_matrix)은 매우 다양한 형태로 나타난다는 것을 알 수 있음.)
http://blog.naver.com/mykepzzang/221121796109
(가역성(related: 가역행렬,invertible_matrix)은 매우 다양한 형태로 나타난다는 것을 알 수 있음.)
7. Moore determinant ¶
curr see  Moore_matrix
Moore_matrix
저것의 행렬식은 Moore_determinant_over_a_finite_field
Moore_determinant_over_a_finite_field
다만 Moore_determinant_of_a_Hermitian_matrix도 있음에 주의
Moore_determinant_of_a_Hermitian_matrix도 있음에 주의
저것의 행렬식은
다만
11. 삼중곱과의 관계 및 행렬식의 세 조건 ¶
삼중곱,triple_product과의 관계 (삼중곱은 바로 앞에서 설명함)
그리고 임의의 n차원에서 세 가지 조건을 만족하는 함수가 항상 있으며 그게 바로 determinant라는 ..? chk
그리고 임의의 n차원에서 세 가지 조건을 만족하는 함수가 항상 있으며 그게 바로 determinant라는 ..? chk
See 김도형 http://www.kocw.net/home/search/kemView.do?kemId=1141060 5. (3차원 좌표체계, 내적과 외적) 1h:22m
대충 적으면,
2차원 평면과 그 위의 두 벡터 a1 a2 가 있을 때, 두 벡터로 결정되는 평행사변형의 넓이,area함수 A(a1, a2)가 있으면 A는 다음을 만족
① D(e1, e2)=1
② A(λa1, a2)=λA(a1, a2) 그리고 A(a1, λa2)=λA(a1, a2)
③ A(a1+a2, a2) = A(a1, a1+a2) = A(a1, a2)
이상 2차원 얘기였고
2차원에선 이게 ad−bc 바로 그거이고
3차원에선 벡터가 세개이며 부피,volume
n차원에서도 성립
2차원 평면과 그 위의 두 벡터 a1 a2 가 있을 때, 두 벡터로 결정되는 평행사변형의 넓이,area함수 A(a1, a2)가 있으면 A는 다음을 만족
① D(e1, e2)=1
② A(λa1, a2)=λA(a1, a2) 그리고 A(a1, λa2)=λA(a1, a2)
③ A(a1+a2, a2) = A(a1, a1+a2) = A(a1, a2)
이상 2차원 얘기였고
2차원에선 이게 ad−bc 바로 그거이고
3차원에선 벡터가 세개이며 부피,volume
n차원에서도 성립
12. 비교: 퍼머넌트 permanent ¶
ex. 2x2일 때
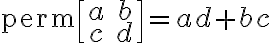
via https://brunch.co.kr/@sjoonkwon0531/21
{
det의 계산은 P class -) 이지만 perm의 계산은 그렇지 않다 - 훨씬 어렵다. 비교적 간단한 square mtx의 perm 계산도 NP-hard.
이지만 perm의 계산은 그렇지 않다 - 훨씬 어렵다. 비교적 간단한 square mtx의 perm 계산도 NP-hard.
}
{
det의 계산은 P class -
}
그리고 determinant와 permanent의 일반화는 이머넌트,immanant ?  Immanant라고 한다. https://mathworld.wolfram.com/Immanant.html
Immanant라고 한다. https://mathworld.wolfram.com/Immanant.html
https://mathworld.wolfram.com/Permanent.htmlhttps://planetmath.org/permanent
}
13. 표기법에 대해 (김홍종) ¶
정사각행렬 A의 행렬식을 기호 det A로 나타내는 대신에 |A|로 쓰는 저자도 있다. 이 편리한(?) 기호는, A의 절댓값을 나타내는 기호와 약간 혼동을 주고, 더 나아가서 치환적분법에서 중요하게 나타나는 행렬식의 절댓값을 ‖A‖로 나타내야 하는 부담을 준다. 우리는 기호 "det A"를 쓰기로 한다. 행렬식을 결정식이라고 부르는 이도 있다.
(김홍종 미적1+ p260 행렬식 각주)
이름은 '결정,determination'에서.
MKL 벡터,vector
(아래의 경우 각각 2x2 행렬의 두 벡터, 3x3 행렬의 세 벡터 얘기)
2D 평면에서 두 벡터를 같은 시점으로 놓아 평행사변형,parallelogram을 만들어 0이 아닌 넓이,area를 가지는가 여부를 결정함.
3D 공간에서 세 벡터를 같은 시점으로 놓아 평행육면체,parallelepiped를 만들어 0이 아닌 부피,volume를 가지는가 여부를 결정함.
(종속(종속성,dependence)이 아닌 독립(독립성,independence)이어야 0이 아닌 저것을 만들 수 있음을 상기)
(이정일 https://youtu.be/hIRveiSlLnY?t=2056)
(아래의 경우 각각 2x2 행렬의 두 벡터, 3x3 행렬의 세 벡터 얘기)
2D 평면에서 두 벡터를 같은 시점으로 놓아 평행사변형,parallelogram을 만들어 0이 아닌 넓이,area를 가지는가 여부를 결정함.
3D 공간에서 세 벡터를 같은 시점으로 놓아 평행육면체,parallelepiped를 만들어 0이 아닌 부피,volume를 가지는가 여부를 결정함.
(종속(종속성,dependence)이 아닌 독립(독립성,independence)이어야 0이 아닌 저것을 만들 수 있음을 상기)
(이정일 https://youtu.be/hIRveiSlLnY?t=2056)
Twins:
행렬식 https://ghebook.blogspot.com/2011/06/determinant.html (어려움)
행렬식의 기하학적 의미 https://ghebook.blogspot.com/2011/06/geometric-meaning-of-determinant.html
https://ratsgo.github.io/linear algebra/2017/05/21/determinants/
3Blue1Brown: The determinant https://www.youtube.com/watch?v=Ip3X9LOh2dk
https://everything2.com/title/Determinant
https://mathworld.wolfram.com/Determinant.html (긺)
![[https]](/123/imgs/https.png) 수학백과: 행렬식
수학백과: 행렬식
 Determinant
Determinant
 행렬식
행렬식
https://planetmath.org/determinant
https://encyclopediaofmath.org/wiki/Determinant
행렬식 https://ghebook.blogspot.com/2011/06/determinant.html (어려움)
행렬식의 기하학적 의미 https://ghebook.blogspot.com/2011/06/geometric-meaning-of-determinant.html
https://ratsgo.github.io/linear algebra/2017/05/21/determinants/
3Blue1Brown: The determinant https://www.youtube.com/watch?v=Ip3X9LOh2dk
https://everything2.com/title/Determinant
https://mathworld.wolfram.com/Determinant.html (긺)
![[https]](/123/imgs/https.png) 수학백과: 행렬식
수학백과: 행렬식https://planetmath.org/determinant
https://encyclopediaofmath.org/wiki/Determinant
Up: 행렬,matrix

