보존계,conservative_system

보존장,conservative_field or 보존벡터장,conservative_vector_field ... QQQ 보존장은 항상 벡터장인지
{
naver 국어사전:

에너지 보존 법칙이 성립하는 힘의 장. 중력장, 전기력장 따위가 있다. 보존장에서 작용하는 힘은 이동 경로에 상관없이 위치에 의해서만 변한다.

mklink
선적분,line_integral 및 선적분의기본정리
기울기,gradient
퍼텐셜함수,potential_function
에너지보존법칙 curr. goto 에너지,energy#s-10
path_independence

https://angeloyeo.github.io/2020/10/01/path_independence.html 1. 끝부분: 경로,path에 관계없이 시작점과 끝점이 같은 서로 다른 경로를 선적분,line_integral해주었을 때 값이 같다면 보존장이라고 할 수 있다고.

퍼텐셜함수로부터 이끌어 낼 수 있는(derivable) 벡터장을 보존장이라고 한다.

A vector field 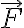$\vec{F}$ is conservative if it is derivable from a potential function. This means that for some scalar field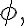 $\phi,$

$\vec{F}=\nabla\phi=\frac{\partial\phi}{\partial x}i+\frac{\partial\phi}{\partial y}j+\frac{\partial\phi}{\partial z}k.$

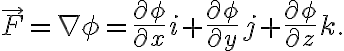
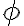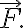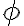We call $\phi$ a potential function, or potential, for $\vec{F}.$ 물론 $\phi$ 가 퍼텐셜이면 임의의 상수를 더한 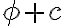$\phi+c$ 도 마찬가지.

(O'Neil 7e 12.4 Independence of Path and Potential Theory p380)

(보존장은 특수한 종류의 벡터장임.)

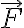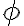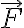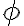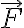2차원 또는 3차원 벡터함수,vector_function $\vec{F}$ 가 스칼라함수 $\phi$ 의 기울기벡터,gradient_vector로 나타나면 $\vec{F}$ 를 보존적(conservative)이라 하고, 이 때 스칼라함수 $\phi$ 를 $\vec{F}$ 의 퍼텐셜함수,potential_function라고 부른다.

다시 말해 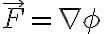$\vec{F}=\nabla\phi$ 를 만족하는 함수 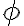$\phi$ 가 존재하면 벡터(벡터함수가 아니라 벡터라 칭해도 옳은지?) 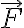$\vec{F}$ 는 보존적이다. 보존적 벡터장을 기울기 벡터장(gradient vector field)이라 부르기도 한다.

(Zill 6e ko 정의 9.9.1 전후, p654)

Twins:

Up:

벡터장,vector_field? 보존장은 항상 벡터장 맞음?
보존,conservation

}

Conservative_system은 수학의 dynamical system 얘기!! (dissipative system 반대)
https://everything2.com/title/conservative system (tmp)

VeryGoodWiki