(정의) 함수 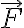 가 영역
가 영역  에서 정의된 벡터장,vector_field이고,
에서 정의된 벡터장,vector_field이고,
 에서 정의된 어떤 스칼라함수,scalar_function
에서 정의된 어떤 스칼라함수,scalar_function  에 대하여
에 대하여
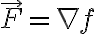
이면, 함수  는
는 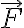 에 대한 퍼텐셜 함수(potential function)라고 부른다.
에 대한 퍼텐셜 함수(potential function)라고 부른다.
(Thomas 13e ko)
어떤 벡터장,vector_field 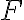 에 대해,
에 대해,
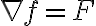
인 미분가능함수,differentiable_function  가 존재할 때,
가 존재할 때,
이런 를
를 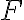 의 잠재함수(potential function)라고 한다.
의 잠재함수(potential function)라고 한다.
여기서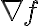 는
는  의 기울기벡터,gradient_vector를 가리킨다.
의 기울기벡터,gradient_vector를 가리킨다.
이런
여기서
Ex. 벡터장 =\langle 2x,2y \rangle) 의 경우,
의 경우,
=x^2+y^2) 에 대해
에 대해
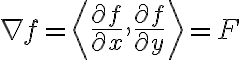
임을 확인할 수 있으므로,  는
는 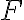 의 잠재함수이다.
의 잠재함수이다.
(수학백과)
관련있다고 추정: (나중에 적절히 link, related/ see also 등으로)
보존장,conservative_field
보존장,conservative_field
curr goto 보존계,conservative_system
보존력,conservative_force기울기,gradient
기울기벡터,gradient_vector?
방향도함수,directional_derivative?
선적분,line_integral?
벡터장,vector_field?
기울기벡터,gradient_vector?
방향도함수,directional_derivative?
선적분,line_integral?
벡터장,vector_field?
potential_gradient - 한글이름정하면 link later; curr goto 전위
tmp links:
https://m.blog.naver.com/cindyvelyn/221821104219
{
스칼라장,scalar_field 의 기울기,gradient 인 벡터장,vector_field
의 기울기,gradient 인 벡터장,vector_field 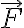 를 보존벡터장,conservative_vector_field이라 하며,
를 보존벡터장,conservative_vector_field이라 하며,
여기서 를 퍼텐셜함수라고 한다.
를 퍼텐셜함수라고 한다.
}
{
스칼라장,scalar_field
여기서
gradient and 잠재함수 (bos의 스터디룸)
https://m.blog.naver.com/bmw9707121/221598732182
{
https://m.blog.naver.com/bmw9707121/221598732182
{
F = grad f = ∇ f이면 f는 벡터장 F의 퍼텐셜 함수임.
}
....
벡터장,vector_field 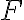 가 어떤 함수
가 어떤 함수  의 기울기,gradient이면, 즉
의 기울기,gradient이면, 즉
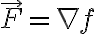
이면
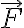 는 "conservative vector field"
는 "conservative vector field"  보존벡터장
보존벡터장  Conservative_vector_field .....curr goto 보존계,conservative_system
Conservative_vector_field .....curr goto 보존계,conservative_system
 는 퍼텐셜함수
는 퍼텐셜함수
Etc ¶
자료구조,data_structure분야에서 potential function의 뜻: See https://xlinux.nist.gov/dads/HTML/potentialfnc.html
퍼텐셜함수(대한수학회 번역) AKA 포텐셜함수, 잠재함수(수학백과)
https://everything2.com/title/potential function
https://encyclopediaofmath.org/wiki/Potential - potential function
![[https]](/123/imgs/https.png) 수학백과: 잠재함수
수학백과: 잠재함수
https://encyclopediaofmath.org/wiki/Potential - potential function
![[https]](/123/imgs/https.png) 수학백과: 잠재함수
수학백과: 잠재함수
