대충
양쪽 끝 두 점과 그 사이 점을 생각, 양쪽 끝 두 점의 weighted_average(할선,secant_line?)와 그 사이 x의 함수값 f(x)을 생각, 이 두 점의 y 좌표를 비교해서, "항상" 크거나(>)/작거나(<)/같음또는크거나(≥)/같음또는작거나(≤)/같거나(=) 이걸로 convex function인지 concave function인지 그리고 strict인지 아닌지, 여부가 정해지는? ( Convex_function and 내 생각, chk)
Convex_function and 내 생각, chk)
양쪽 끝 두 점과 그 사이 점을 생각, 양쪽 끝 두 점의 weighted_average(할선,secant_line?)와 그 사이 x의 함수값 f(x)을 생각, 이 두 점의 y 좌표를 비교해서, "항상" 크거나(>)/작거나(<)/같음또는크거나(≥)/같음또는작거나(≤)/같거나(=) 이걸로 convex function인지 concave function인지 그리고 strict인지 아닌지, 여부가 정해지는? (
From 수학백과: 옌센 부등식 ¶
실수 구간에서 정의된 함수  가 ‘아래로 볼록’ 혹은 ‘볼록함수’라는 것은,
가 ‘아래로 볼록’ 혹은 ‘볼록함수’라는 것은,
구간 내 임의의 두 점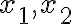 와
와 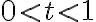 인 임의의 실수
인 임의의 실수 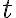 에 대해 다음 부등식,inequality이 성립한다는 것.
에 대해 다음 부등식,inequality이 성립한다는 것.
x_2)\le tf(x_1)+(1-t)f(x_2))
여기서 (부등식의) 등호가 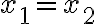 일 때만 성립하면 순볼록함수라고 한다.
일 때만 성립하면 순볼록함수라고 한다.
구간 내 임의의 두 점
(옌센_부등식,Jensen_inequality 설명에 앞선 내용)
tmp cleanup ¶
/*from ![[https]](/123/imgs/https.png) this slide p2*/
this slide p2*/
{
A function is said to be convex(볼록한) over an interval)
if for every) and
and 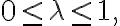
x_2)\le\lambda f(x_1)+(1-\lambda)f(x_2))
A function  is said to be strictly convex(순볼록) if equality holds only if
is said to be strictly convex(순볼록) if equality holds only if 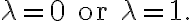
![[https]](/123/imgs/https.png) this slide p2*/
this slide p2*/{
A function is said to be convex(볼록한) over an interval
if for every
(생각: 선형성,linearity 둘 중의 하나와 식의 모양이 비슷하다. 다만 등호가 아니고 부등호다.)
Thm:
함수 가 모든 점에서
가 모든 점에서
함수
음이 아닌(non-negative) 이계도함수를 가지면, 함수는 볼록(convex).
양인(positive) 이계도함수를 가지면, 함수는 순볼록(strictly convex).
}양인(positive) 이계도함수를 가지면, 함수는 순볼록(strictly convex).
Excerpt: 김홍종 ¶
구간,interval 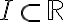 에서 정의된 실가(real valued) 함수
에서 정의된 실가(real valued) 함수  가 볼록함수라는 것은
가 볼록함수라는 것은
구간 의 임의의 두 점
의 임의의 두 점  에 대하여 구간
에 대하여 구간 ![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) 에서 함수
에서 함수  의 그래프가 이 그래프의 양끝점을 이은 선분,line_segment보다 아래쪽에 있다는 것을 뜻한다.
의 그래프가 이 그래프의 양끝점을 이은 선분,line_segment보다 아래쪽에 있다는 것을 뜻한다.
다시 표현하면,
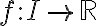 이 볼록함수라는 것은 구간의 임의의 두 점
이 볼록함수라는 것은 구간의 임의의 두 점  와 임의의
와 임의의 ![$t\in[0,1]$ $t\in[0,1]$](/123/cgi-bin/mimetex.cgi?\Large t\in[0,1]) 에 대하여
에 대하여
a+tb)\le(1-t)f(a)+tf(b))
인 함수를 말한다.
이와 같은 정의에서는 상수함수,constant_function도 볼록함수이다. 상수함수를 제외하려면 부등호 '<'를 사용한 순볼록함수를 정의하면 된다.
함수) 가 연속인 경우에는,
가 연속인 경우에는, ) 가 볼록함수일 필요충분조건은
가 볼록함수일 필요충분조건은
 \le \frac{f(a)+f(b)}{2})
이다.
함수) 가 미분가능한 경우에는,
가 미분가능한 경우에는, ) 가 볼록함수일 필요충분조건은 도함수
가 볼록함수일 필요충분조건은 도함수 ) 가 증가함수인 것이다.
가 증가함수인 것이다.
함수) 가 두번 미분가능한 경우에는,
가 두번 미분가능한 경우에는, ) 가 볼록함수일 필요충분조건은
가 볼록함수일 필요충분조건은 \ge 0) 이다.
이다.
구간
다시 표현하면,
이와 같은 정의에서는 상수함수,constant_function도 볼록함수이다. 상수함수를 제외하려면 부등호 '<'를 사용한 순볼록함수를 정의하면 된다.
함수
함수
함수
(김홍종 미적1+ p390, 부록 수학사전)
Twins:
 Convex_function
Convex_function
https://mathworld.wolfram.com/ConvexFunction.html
https://developers.google.com/machine-learning/glossary?hl=ko#convex-function
 볼록_함수
볼록_함수
 Convex_function
Convex_function
https://ratsgo.github.io/convex optimization/2017/12/26/convexfunction/
https://ncatlab.org/nlab/show/convex function
https://mathworld.wolfram.com/ConvexFunction.html
https://developers.google.com/machine-learning/glossary?hl=ko#convex-function
https://ratsgo.github.io/convex optimization/2017/12/26/convexfunction/
https://ncatlab.org/nlab/show/convex function

