Jensen’s inequality, 젠센 부등식 (kms) 옌센 부등식 (wpko)
오목볼록(오목볼록,concave_and_convex)과 연관. - curr goto 미적분,calculus#s-9 <- 저기에도 설명 있음.
오목볼록과 매우 밀접. see https://suhak.tistory.com/221 (볼록 함수와 젠센 부등식)
볼록함수,convex_function
오목볼록과 매우 밀접. see https://suhak.tistory.com/221 (볼록 함수와 젠센 부등식)
볼록함수,convex_function
(대충) // 나중에 엄밀하게 rewrite
볼록함수에 대하여,
값들의 평균을 함수에 대입한 결과는
값들을 각각 함수에 대입하여 평균을 낸 것보다
작거나 같다는 것.
i.e.
값들을 (모두) 평균하여 함수에 대입한 결과는
값들을 (각각) 대입하여 평균을 낸 것보다
이하라는 것.
볼록함수에 대하여,
값들의 평균을 함수에 대입한 결과는
값들을 각각 함수에 대입하여 평균을 낸 것보다
작거나 같다는 것.
i.e.
값들을 (모두) 평균하여 함수에 대입한 결과는
값들을 (각각) 대입하여 평균을 낸 것보다
이하라는 것.
위로 오목(concave up) (i.e. 아래로 볼록)한 함수  에 대한 성질로,
에 대한 성질로,
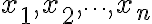
의 가중평균,weighted_mean(curr see 가중값,weight)의 함수값이
,f(x_2),\cdots,f(x_n)) 의 가중평균 이하라는 것
의 가중평균 이하라는 것
}
// tmp from wpko; merge.
{
기대값의 볼록함수와 볼록함수의 기대값 사이의 부등식 관계.
(see 기대값,expected_value, 볼록함수,convex_function)
}
{
기대값의 볼록함수와 볼록함수의 기대값 사이의 부등식 관계.
(see 기대값,expected_value, 볼록함수,convex_function)
}
// 수학백과
볼록함수 가 만족하는 부등식은 다음과 같다.
가 만족하는 부등식은 다음과 같다.
x_2)\le tf(x_1)+(1-t)f(x_2))
여기서
(부등식의) 등호가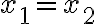 일 때만 성립하면
일 때만 성립하면  는 순볼록함수라고 한다.
는 순볼록함수라고 한다.
볼록함수
(부등식의) 등호가
이것을 일반화한 것이 옌센 부등식.
\le t_1f(x_1)+t_2f(x_2)+\cdots+t_nf(x_n))
여기서
 : 실수 구간에서 정의된 볼록함수
: 실수 구간에서 정의된 볼록함수
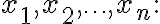 구간 내 임의의 점
구간 내 임의의 점
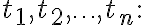 0보다 크고 합이 1인 실수들 // rel. partition_of_unity ?
0보다 크고 합이 1인 실수들 // rel. partition_of_unity ?
 가 순볼록함수이면 등호는
가 순볼록함수이면 등호는 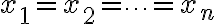 일 때만 성립한다.
일 때만 성립한다.
즉 (Jensen 부등식)은 (볼록함수의 조건이 되는 부등식)을 일반화한 것? chk
확률변수의 Jensen inequality
/*from ![[https]](/123/imgs/https.png) this slide p2*/
this slide p2*/
If is a 볼록함수,convex_function and
is a 볼록함수,convex_function and  is a 확률변수,random_variable, then
is a 확률변수,random_variable, then
\ge f(EX))
Moreover(게다가/더욱이), if  is strictly convex(순볼록), then equality implies that
is strictly convex(순볼록), then equality implies that 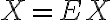 with probability 1, i.e.
with probability 1, i.e.  is a constant.
is a constant.
![[https]](/123/imgs/https.png) this slide p2*/
this slide p2*/If
// from 수학백과 (증명은 수학백과에)
 가 확률변수이고,
가 확률변수이고,  가
가  의 값을 포함하는 구간,interval에서 정의된 볼록함수,convex_function일 때, 다음 부등식이 성립.
의 값을 포함하는 구간,interval에서 정의된 볼록함수,convex_function일 때, 다음 부등식이 성립.
) \le E(f(X)))
Twins:
![[https]](/123/imgs/https.png) 수학백과: 옌센 부등식
수학백과: 옌센 부등식
https://everything2.com/title/Jensen inequality
 옌센_부등식
옌센_부등식
 Jensen's_inequality
Jensen's_inequality
![[https]](/123/imgs/https.png) https://www.probabilitycourse.com/chapter6/6_2_5_jensen%27s_inequality.php
https://www.probabilitycourse.com/chapter6/6_2_5_jensen%27s_inequality.php
https://mathworld.wolfram.com/JensensInequality.html
https://encyclopediaofmath.org/wiki/Jensen_inequality
 젠센 부등식
젠센 부등식
![[https]](/123/imgs/https.png) 수학백과: 옌센 부등식
수학백과: 옌센 부등식https://everything2.com/title/Jensen inequality
![[https]](/123/imgs/https.png) https://www.probabilitycourse.com/chapter6/6_2_5_jensen%27s_inequality.php
https://www.probabilitycourse.com/chapter6/6_2_5_jensen%27s_inequality.phphttps://mathworld.wolfram.com/JensensInequality.html
https://encyclopediaofmath.org/wiki/Jensen_inequality
Up: 부등식,inequality

