스토크스_정리,Stokes_theorem


스토크스 정리는 그린 정리를 3차원으로 확장한 것.
스토크스 정리는 한차원 높은 그린 정리라 할 수 있음.
그린_정리,Green_theorem는 스토크스 정리의 특수한 경우.

[edit]

Ulaby

면적분과 선적분의 관계?

Stokes's theorem converts the 면적분,surface_integral of the 회전,curl of a vector over an open surface S into a 선적분,line_integral of the vector along the contour C bounding the surface S.
$\int_S(\nabla\times\vec{B})\cdot d\vec{s}=\oint_C \vec{B}\cdot d\vec{\ell}$

(Ulaby 7e p166 3-6.2)

[edit]

정길수

바깥곡선을 따라 한 일 선적분,line_integral은
$\oint \vec{A}d\ell$
곡면에서, 안쪽 원들에서 각각의 회전에 대해 $\text{curl}\vec{A}$ 를 구하고 그것과 면에 내적
$\iint \text{curl}\vec{A}\cdot ds$
를 구하면 선적분과 같다는 정리가 스톡스 정리

$\iint \text{curl}\vec{A} ds=\oint \vec{A}d\ell$
정적분의 값을 찾는 다음 정리와 관련? 일반화?
$f:[a,b]$ 에서 연속, $F:f$ 의 역도함수
$\Rightarrow\;\int_a^b f(x)dx=F(b)-F(a)$
3차원 공간 상의 매끄러운 곡면 위에서 벡터장,vector_field의 회전,curl을 적분한 값이 그 곡면의 경계인 폐곡선에서 벡터장을 선적분,line_integral한 값과 같다는 정리.

면(곡면,surface) S를 곡선,curve C가 둘러싸고 있을 때
$\oint_C \vec{F}\cdot d\vec{r} = \int_S\nabla\times\vec{F}\cdot d\vec{S}=0$

=0?

선적분한 값 = 면적분한 값

어떤 벡터장,vector_field $\vec{A}$ 가 있고,
폐경로(폐곡선)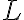 $L$ 이 있고 그 위를 지나는 미소길이가 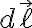$d\vec{\ell}$ 이고,
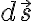폐경로에 의해 만들어지는 표면 $S$ 가 있으며, 그 부분인 미소면적 $d\vec{s}$ 에서 발생하는 A의 회전 $(\nabla\times\vec{A})$ 이 있을 때
$\oint_L\vec{A}\cdot d\vec{\ell} = \int_S \nabla\times\vec{A} d\vec{s}$
선적분 = 면적분 값이 같다.
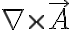S 전체에 걸쳐 $\vec{A}$ 와 $\nabla\times\vec{A}$ 가 연속일 때, 폐경로 L에(sic, 의?) 주위의 벡터장 $\vec{A}$ 의 회전은 L을 주변으로 하는 개구면(? 개=開) S에 대한 $\vec{A}$ 의 회전을 면적분,surface_integral한것과 같다.

tmp from [https]전전공부방
$\oint_C\vec{F}\cdot d\vec{r}=\int_S(\nabla\times\vec{F})\cdot d\vec{a}$
S는 가장자리가 폐곡선 C인 면
이 정리는 임의의 폐곡선에 대해 항상 성립 (일종의 항등식,identity?)
(여기서 S는 가장자리만 폐곡선 C이면 어떤 것이라도 OK)

Stokes 정리와 다이버전스 정리(발산정리,divergence_theorem)
Stokes thm: 폐곡선에 대한 선적분을 면적분으로
$\oint_C \vec{F}\cdot d\vec{r}=\int_S(\nabla\times\vec{F})\cdot d\vec{a}$
Divergence thm: 폐곡면에 대한 면적분을 부피적분으로
$\oint_S \vec{F}\cdot d\vec{a}=\int_V(\nabla\cdot\vec{F})dv$

2020-09-16 from 차동우: 스토크스 정리와 다이버젠스 정리 https://youtu.be/Sa7xDuWEvZ4 13m
스토크스 정리와 다이버젠스 정리

임의의 벡터 $\vec{A}$ 에 대해
$\iiint_V\nabla\cdot\vec{A}dV=\iint_S\vec{A}\cdot\hat{n}dS$
가 성립 (Gauss' 정리)

가우스 정리와 비슷하게
$\oint\vec{A}\cdot d\vec{r}=\iint_S\nabla\times\vec{A}\cdot\hat{n} dS$
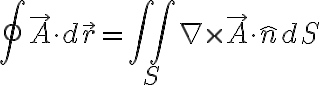
가 성립 (Stokes' 정리)

from [https]박석재 마지막부분
DELME

$S$ 는 조각마다 매끄러운 유향 곡면
$C$ 는 그 경계이며 조각마다 매끄러운 단순 폐곡선
$F$ 는 벡터장
그 성분들의 연속인 편도함수가 $S$ 를 포함하는 ℝ3의 열린 영역에서 존재

그러면 다음이 성립:
$\int\nolimits_C F\cdot dr = \iint\nolimits_S \operatorname{curl} F \cdot dS$

[https]src
MKL
경로에 의존하지 않는다는 점에서
보존력,conservative_force
과 관련????


$\oint \vec{V}\cdot d\vec{\ell} = \int_S (\nabla\times\vec{V})\cdot d\vec{S}$

$S:$ 폐곡면
$\nabla\times\vec{V}\ne 0$ - 즉 $V$ 는 회전성이 있는 vector field

대략적 의의는
그런 벡터장의 curl을 면적분한 값이(우변),
그 벡터장을 그냥 둘레를 따라 선적분한 값과(좌변)
같다는 것. 좌변이 더 계산하기 간단.

이건 나중에...
$\int_M d\omega = \int_{\partial M}\omega$

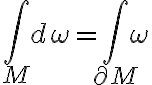
e2에 따르면,
$M:$ differential_manifold with boundary $\partial M$
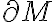
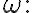$\omega:$ 미분형식,differential_form이며 order는 M의 차원보다 하나 작은
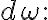$d\omega:$ 그것(omega?)의 외미분,exterior_derivative