Maxwell's equations
2. 이름 ¶
1~4 각 법칙의 이름이 다양함.
| 1 | 2 | 3 | 4 | source |
| 가우스 법칙 | 가우스 자기 법칙 | 패러데이 전자기 유도 법칙 | Ampère's circuital law | |
| 전기장의 가우스 법칙 | 자기장의 가우스 법칙 | 패러데이_법칙,Faraday_s_law | 맥스웰이 수정한 앙페르 법칙 | 바로 아래 |
| 앙페르-맥스웰 법칙 Ampere-Maxwell's law | ||||
| Gauss' law | Gauss' law for magnetic fields | Faraday's law | Ampere's law | 아래 maxwell-equ~.com |
| 전기장에 대한 가우스 법칙 | 자기장에 대한 가우스 법칙 |
3. table ¶
![[https]](/123/imgs/https.png) from from | 이희원 | 송종현 | |
| 전기장의 가우스 법칙 | |||
| 자기장의 가우스 법칙 | |||
| 패러데이_법칙,Faraday_s_law | |||
| 맥스웰이 수정한 앙페르 법칙 (앙페르의 법칙을 수정보완한 법칙, 맥스웰에 의해 개선된 앙페르의 법칙) |
4. Fleisch ¶
Gauss's law. 가우스의 전기장 법칙. 설명은 전하,electric_charge 맨 앞에 달음.
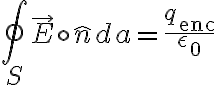
여기서
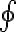 : 폐곡면(closed_surface)에 대한 적분임을 상기
: 폐곡면(closed_surface)에 대한 적분임을 상기
 : 곡면
: 곡면
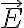 : 전기장,electric_field은 벡터임을 상기
: 전기장,electric_field은 벡터임을 상기
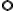 : 스칼라곱,scalar_product,dot_product은 E가 n에 평행인 (면에 수직인) 부분을 찾는 방법
: 스칼라곱,scalar_product,dot_product은 E가 n에 평행인 (면에 수직인) 부분을 찾는 방법
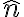 : 곡면에 수직인 단위벡터,unit_vector
: 곡면에 수직인 단위벡터,unit_vector
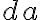 : 곡면 면적의 증분(increment)
: 곡면 면적의 증분(increment)
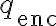 : 곡면 내부 전하 (enc=enclosed. 이것은 total charge, net charge)
: 곡면 내부 전하 (enc=enclosed. 이것은 total charge, net charge)
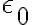 : 자유공간유전율,permittivity
: 자유공간유전율,permittivity
Gauss's law for magnetic fields (integral form).
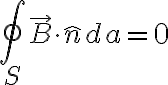
The total magnetic flux passing through any closed surface is zero.
여기서
여기서
5. 최준곤 ¶
| 1 | 쿨롱_법칙,Coulomb_s_law: Force between charges (gravity와 비슷) | 아래 가우스법칙과 같은 결과 |
| 2 | 가우스_법칙,Gauss_s_law: Relation between charges and electric field | 맥스웰 1, 2 법칙 |
| 3 | 패러데이_법칙,Faraday_s_law of induction: Time change of B inducing change of E | 맥스웰 3법칙 |
| 4 | 앙페르_법칙,Ampere_s_law Ampere-Maxwell's law: Time change of E inducing change of B | 맥스웰 4법칙 |
from http://www.kocw.net/home/search/kemView.do?kemId=1032191
6. 조성호 물리 돋보기 ¶
1. 전기장,electric_field에 대한 가우스_법칙,Gauss_s_law
2. 자기장,magnetic_field에 대한 가우스 법칙
2. 자기장,magnetic_field에 대한 가우스 법칙
시간적으로 변하지 않는 자기장을 만드는 자하,magnetic_charge는 존재하지 않는다.
3. 패러데이의 전자기유도 법칙 (패러데이_법칙,Faraday_s_law)자기장이 시간적으로 변하면 전기장이 생긴다.
4. 맥스웰이 수정한 앙페르_법칙,Ampere_s_law7. Sadiku 전자기학 5e (번역판) 4p에서 ¶
D = 전속밀도 (See 전속밀도,electric_flux_density)
B = 자속밀도 (See 자속밀도,magnetic_flux_density)
E = 전기장의 세기 (See 전기장세기,electric_field_intensity)
H = 자기장의 세기 (See 자기장세기,magnetic_field_intensity)
ρv = 체적전하밀도 (See 전하밀도,charge_density)
J = 전류밀도 (See 전류밀도,current_density)
B = 자속밀도 (See 자속밀도,magnetic_flux_density)
E = 전기장의 세기 (See 전기장세기,electric_field_intensity)
H = 자기장의 세기 (See 자기장세기,magnetic_field_intensity)
ρv = 체적전하밀도 (See 전하밀도,charge_density)
J = 전류밀도 (See 전류밀도,current_density)
8. Schaum Electromagnetics 4e p11 에서 ¶
위의 식은 순서대로 각각
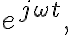 also called time harmonics), we obtain the 위상자,phasor representation (also called the time harmonic form):
also called time harmonics), we obtain the 위상자,phasor representation (also called the time harmonic form):
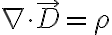
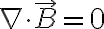
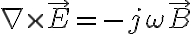
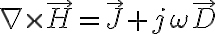
(can be used without loss of generality)
- Gauss's law(가우스_법칙,Gauss_s_law) for the electric field
- Gauss's law for the magnetic field
- Faraday's law(패러데이_법칙,Faraday_s_law)
- Ampere's law(앙페르_법칙,Ampere_s_law) supplemented by Maxwell's 변위전류,displacement_current
9. from SNUON_물리의 기본2: ∇, ∫를 쓰지 않은 서술 ¶
1. 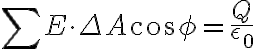
2.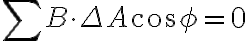
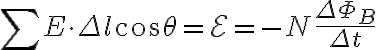
4.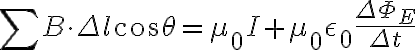
다시 말해
2.
가우스 법칙을 자기장에 적용하면 0
3. 4.
다시 말해
| Gauss' law | 가우스_법칙,Gauss_s_law | |
| No magnetic charge | ||
| Faraday's law | 패러데이_법칙,Faraday_s_law | |
Maxwell's intuition: | Ampere's law | 앙페르_법칙,Ampere_s_law |
In vacuum,
| 미분형 | 적분형 | |
| | ||
| | ||
| | ||
| |
| 전기장,electric_field | |
| 자기장,magnetic_field 중에서 자속밀도,magnetic_flux_density | |
| 진공의 유전율,permittivity | |
| 진공의 투자율,permeability | |
| 전류밀도,current_density ?? |
13. 차동우 ¶
일단,
Divergence thm
\cdot d\vec{a}=\int_V\nabla\cdot\vec{F}(\vec{r})dv)
임의의 벡터장 F(r)에 대해 임의의 폐곡면 S에 대해 성립
Stokes thm
\cdot d\vec{r}=\int_S(\nabla\times\vec{F}(\vec{r}))\cdot d\vec{a})
임의의 벡터장 F(r)에 대해 임의의 폐곡선 C에 대해 성립
발산정리,divergence_theorem
스토크스_정리,Stokes_theorem
임의의 벡터장 F(r)에 대해 임의의 폐곡면 S에 대해 성립
임의의 벡터장 F(r)에 대해 임의의 폐곡선 C에 대해 성립
스토크스_정리,Stokes_theorem
from 물리학 07주차 04 미분형태의 맥스웰 방정식 https://youtu.be/UWaoLpdW2BM
....이하 안적음 TBW
todo 물리학 07주차 03 맥스웰 방정식 https://youtu.be/7RBCsTxQwnI
14. Ulaby ¶
정전기학,electrostatics일 경우
첫번째 식은 그대로
두번째 식은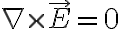
정자기학,magnetostatics의 경우두번째 식은
세번째 식은 그대로
네번째 식은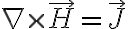
그리하여 이 때는 E-B, D-H 관계가 사라지는(? CHK) 것을 볼 수 있으며 책에는 다음과 같이 써 있다. Electric and magnetic fields become decoupled in the static case.네번째 식은
(Ulaby 7e p179 4-1)
15. ghebook ¶
https://ghebook.blogspot.com/2010/09/maxwells-equations.html
원문:
쿨롱의 법칙: 전속 밀도(electric flux density)의 원천을 검출하면 그 값은 전하 밀도(electric charge density)가 된다.
패러데이의 법칙: 전기장(electric field)의 회전을 검출하면 그 값은 자속 밀도(magnetic flux density)의 시간적 감소와 같다.
비오–사바르의 법칙: 자속 밀도의 원천을 검출하면 그 값은 항상 0이 된다.
암페어의 법칙: 자기장(magnetic field)의 회전을 검출하면 그 값은 전류 밀도(electric current density) 그 자체 혹은 전속 밀도의 시간적 증가와 같다.
| 쿨롱_법칙,Coulomb_s_law | 전속밀도,electric_flux_density(D)의 원천을 검출하면 그 값은 전하밀도,charge_density가 된다 |
| 패러데이_법칙,Faraday_s_law | 전기장,electric_field의 회전,curl을 검출하면 그 값은 자속밀도,magnetic_flux_density(B)의 시간적 감소와 같다 |
| 비오-사바르_법칙,Biot-Savart_law | 자속밀도,magnetic_flux_density의 원천을 검출하면 항상 0이 된다 |
| 앙페르_법칙,Ampere_s_law | 자기장,magnetic_field의 회전,curl을 검출하면 그 값은 전류밀도,current_density 그 자체 혹은 전속밀도,electric_flux_density(D)의 시간적 증가와 같다 |
쿨롱의 법칙: 전속 밀도(electric flux density)의 원천을 검출하면 그 값은 전하 밀도(electric charge density)가 된다.
패러데이의 법칙: 전기장(electric field)의 회전을 검출하면 그 값은 자속 밀도(magnetic flux density)의 시간적 감소와 같다.
비오–사바르의 법칙: 자속 밀도의 원천을 검출하면 그 값은 항상 0이 된다.
암페어의 법칙: 자기장(magnetic field)의 회전을 검출하면 그 값은 전류 밀도(electric current density) 그 자체 혹은 전속 밀도의 시간적 증가와 같다.
16. Sites ¶
| 1 | | Gauss' law |
| 2 | | Gauss' law for magnetic fields |
| 3 | | Faraday's law |
| 4 | | Ampere's law |
Intuitive Guide to Maxwell's Equations
https://github.com/photonlines/Intuitive-Guide-to-Maxwells-Equations
https://news.ycombinator.com/item?id=23700295
https://github.com/photonlines/Intuitive-Guide-to-Maxwells-Equations
https://news.ycombinator.com/item?id=23700295
Twins/further refs
 맥스웰_방정식
맥스웰_방정식
https://namu.wiki/w/맥스웰 방정식
https://librewiki.net/wiki/맥스웰_방정식
http://physica.gsnu.ac.kr/phtml/electromagnetic/emwave/maxwell/maxwell.html
![[http]](/123/imgs/http.png) http://wiki.mathnt.net/index.php?title=맥스웰_방정식
http://wiki.mathnt.net/index.php?title=맥스웰_방정식
https://everything2.com/title/Maxwell%27s Equations
https://namu.wiki/w/맥스웰 방정식
https://librewiki.net/wiki/맥스웰_방정식
http://physica.gsnu.ac.kr/phtml/electromagnetic/emwave/maxwell/maxwell.html
![[http]](/123/imgs/http.png) http://wiki.mathnt.net/index.php?title=맥스웰_방정식
http://wiki.mathnt.net/index.php?title=맥스웰_방정식https://everything2.com/title/Maxwell%27s Equations

