1. 물1 전자기유도 단원에서 ¶
균일한 자기장에 폐회로 도선이 있다고 가정.
이 회로면을 수직으로 지나는 총 자기장의 양은, 회로면 넓이 A와 회로면에 수직방향의 자기장 성분 B⊥의 곱인데 이것을 자기력선속 또는 자속,magnetic_flux이라 함.
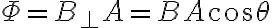
Faraday는 폐회로에 유도되는 전류의 세기가 회로면에서 자속의 시간적 변화율에 비례함을 발견. 즉 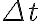 동안 자속이
동안 자속이 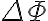 만큼 변했다면 회로에 유도되는 유도전류
만큼 변했다면 회로에 유도되는 유도전류  는
는
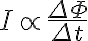
N번 감긴 코일에서 회로면의 넓이는 단면적의 N배가 되므로, 자속도 N배가 되므로,
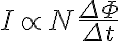
이것이 패러데이_법칙,Faraday_s_law.
이 회로면을 수직으로 지나는 총 자기장의 양은, 회로면 넓이 A와 회로면에 수직방향의 자기장 성분 B⊥의 곱인데 이것을 자기력선속 또는 자속,magnetic_flux이라 함.
N번 감긴 코일의 자속은 Φ=BA 가 아닌 Φ=NBA 가 되어야 함 CHK
렌츠_법칙,Lenz_s_law 생략.
패러데이 법칙과 렌츠 법칙으로 회로에 유도되는 전압,voltage V는 이렇게 나타낼 수 있음.
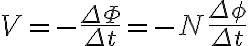
(sic. 이 책에서 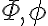 에 다른 의미를 부여한 듯)
에 다른 의미를 부여한 듯)
(-) 부호 : 유도전류의 방향, 자속 변화를 방해하는 방향을 의미

