AKA 자기선속, 자기력선속, 자기플럭스, 자기다발
기호:
단위:
단위:
Wb (weber)
1 Wb = 1 T·m2 (Φ=B·A에서)
자기력선의 묶음, hence the name ? CHK1 Wb = 1 T·m2 (Φ=B·A에서)
유도전류,induced_current에도 정의 있음. (물1)
면적 A를 지나는 자속(ΦM)은,  에서 면적 A에 수직인 성분 B1 과 A의 곱으로 정의.
에서 면적 A에 수직인 성분 B1 과 A의 곱으로 정의.
도선 고리로 둘러싸인 폐곡면(or 면적)에 시간에 대한 자속 변화가 있으면 유도기전력,induced_emf이 발생.
ΦM = B1 A = B A cos(θ)
θ는 자기장 방향과 면적에 수직인 방향 사이 각.도선 고리로 둘러싸인 폐곡면(or 면적)에 시간에 대한 자속 변화가 있으면 유도기전력,induced_emf이 발생.
TBW:
자기력선과의 관계
자기장과의 관계
 에서 면적 A를 지나가는 자기다발 ΦB는
에서 면적 A를 지나가는 자기다발 ΦB는
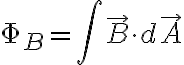
로 정의하며,  가 어떤 면전에 수직하고 균일할 때 자기다발은
가 어떤 면전에 수직하고 균일할 때 자기다발은
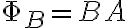
자기력선과의 관계
자기장과의 관계
자속은 자기장의 세기를 표현?
밑에 내용 있음
자기력과의 관계밑에 내용 있음
자속=어떤 가상의 곡면(단면)에 작용하는 총 자기력?
자기장 2. 면적(A), 자기장,magnetic_field esp. 자속밀도,magnetic_flux_density(B) 와의 관계 ¶
Φ=AB, B=Φ/A, 즉 자속밀도=자속/면적
자기장(자속밀도, B)의 단위는 T (tesla)
더 일반적? 으로는,
면을 통과하는 자속 Φ은 자기장에 수직하게 투영된 면적 Acosθ에 자기장 B의 곱
면을 통과하는 자속 Φ은 자기장에 수직하게 투영된 면적 Acosθ에 자기장 B의 곱
Φ = B A cosθ
자속은 자기장을 면적 적분하여 얻어진다.
정의는 패러데이_법칙,Faraday_s_law에도 있음
Faraday's law(패러데이_법칙,Faraday_s_law) states that a changing magnetic flux induces an electric field:

좌변에 스토크스_정리,Stokes_theorem를 적용하고  가 미세한 영역으로 줄어드는(collapse into a tiny region) 극한을 취하면(반지름이
가 미세한 영역으로 줄어드는(collapse into a tiny region) 극한을 취하면(반지름이  인 구 안에 들어가도록)
인 구 안에 들어가도록)

![$\left[ \nabla \times \vec{E} + \frac{\partial \vec B}{\partial t}\right] \cdot \int_S d\vec{\sigma} = 0$ $\left[ \nabla \times \vec{E} + \frac{\partial \vec B}{\partial t}\right] \cdot \int_S d\vec{\sigma} = 0$](/123/cgi-bin/mimetex.cgi?\Large \left[ \nabla \times \vec{E} + \frac{\partial \vec B}{\partial t}\right] \cdot \int_S d\vec{\sigma} = 0)
결과적으로 패러데이 법칙의 미분형을 도출할 수 있다. (맥스웰_방정식,Maxwell_equation의 세번째)

(Y17.3)


![[https]](/123/imgs/https.png)