패러데이는 1831년 자석,magnet이 전기를 발생시킬 수 있다는 사실을 실험으로 확인. 코일과 자석 중 어느 하나가 나머지에 대해 상대적으로 움직이면 코일에 전류가 발생하며 이 현상이 전자기유도이다. 이 때 생기는 전류는 유도전류,induced_current, 이 때 생기는 전압은 유도기전력,induced_emf.
코일 내부 자기장,magnetic_field이 변하면 코일에 전류가 흐르는 현상.
자석,magnet과 코일,coil중 하나가 나머지에 대해 상대적으로 움직이면, 코일에 전류,electric_current가 발생하는 현상.
유도 기전력은 패러데이_법칙,Faraday_s_law에 의해
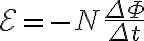
유도기전력은 외부 공급 전류를 방해하는 방향으로 생기므로 역기전력이라고도 함.
유도기전력이 만든 전류는 유도전류,induced_current.
이때 생기는 전류: 유도전류,induced_current { 유도전류의 방향은 ...을 방해하는 방향??? 렌츠_법칙,Lenz_s_law }
이때 생기는 전압: 유도기전력,induced_emf
N회 감긴 코일에 시간 Δt동안 자속,magnetic_flux이 ΔΦ만큼 변하면,이때 생기는 전압: 유도기전력,induced_emf
유도 기전력은 패러데이_법칙,Faraday_s_law에 의해
유도기전력이 만든 전류는 유도전류,induced_current.
코일에 전류 I가 흐르면 코일을 통과하는 자속 Φ는 I에 비례하므로
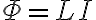
N번 감긴 회로에선
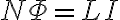
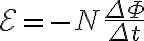
}{\Delta t})
}{\Delta t})
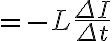
따라서 코일의 자체 유도 기전력(see 유도기전력,induced_emf)을 전류의 변화율로 나타내면

여기서 L은 자체유도계수(자체인덕턴스,self-inductance)
이렇게 회로 전류가 변하여 회로에 기전력이 유도되는 현상을 자체유도,self-induction라고 하며, 이 때의 기전력은 전류 변화를 방해하는 방향으로 생기므로 역기전력이라고도 부름

