패러데이의 유도법칙 (Faraday's law of induction)
유도전류, 자속과의 관계 ¶
패러데이는 폐회로에 유도되는 유도전류 세기가 회로면에서 자속의 시간변화율에 비례한다는 것을 발견.
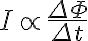
See 유도전류,induced_current and 자속,magnetic_flux
고딩(EBS) ¶
시간 Δt 동안, 감은 수 N인 코일을 통과하는 자속,magnetic_flux 변화가 ΔΦ일 때, 유도 기전력 V는
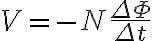
식의 (-) 부호는 유도기전력 방향이 자기선속 변화를 방해하는 방향이라는 의미이므로, 패러데이 법칙은 렌츠_법칙,Lenz_s_law을 포함.
(Richardson)
- - 부호 : 렌츠_법칙,Lenz_s_law
유도기전력은 회로를 통과하는 자기선속의 시간 변화율에 비례한다.
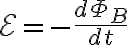
여기서
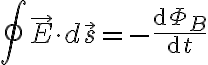
면적 A를 통과하는 자기 다발 ( 자속,magnetic_flux, 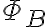 )
)
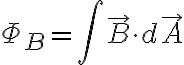
또는
 (균일한 자기장과 편평한 표면, θ:)
(균일한 자기장과 편평한 표면, θ:)
단위는
: 회로에 생긴 유도 기전력,electromotive_force,emf
: 고리의 표면을 지나가는 자기 다발
- - 부호 : 렌츠_법칙,Lenz_s_law
1 T·m² = 1 Wb

