임펄스 응답(impulse response)
표기:
) : continuous-time system impulse response
: continuous-time system impulse response
![$h[n]$ $h[n]$](/123/cgi-bin/mimetex.cgi?\Large h[n]) : discrete-time system impluse response
: discrete-time system impluse response
Sub? :
![$h[n]$ $h[n]$](/123/cgi-bin/mimetex.cgi?\Large h[n]) 샘플만 0이 아니고 나머지는 0임) 무한할 수 있다.
샘플만 0이 아니고 나머지는 0임) 무한할 수 있다.
임펄스 응답의 길이가 유한한 경우 FIR(finite impulse response) 시스템이라 하고, 길이가 무한한 경우 IIR(infinite impulse response) 시스템이라고 한다.
(김명진 신시 p423)
FIR: finite-duration impluse response
IIR: infinite-duration impulse response
... FIR IIR , rel. 필터,filter
FIR IIR , rel. 필터,filter
시스템의 임펄스 응답은 길이가 유한할 수도 있고(즉, 유한한 개수의 IIR: infinite-duration impulse response
...
임펄스 응답의 길이가 유한한 경우 FIR(finite impulse response) 시스템이라 하고, 길이가 무한한 경우 IIR(infinite impulse response) 시스템이라고 한다.
(김명진 신시 p423)
QQQ 이건 항상 단위임펄스응답,unit_impulse_response과 동의어인지 아님 아닌 경우가 있는지?
입력이 ) 일 때, 선형시스템의 출력을
일 때, 선형시스템의 출력을 ![$\ell[x(t)]$ $\ell[x(t)]$](/123/cgi-bin/mimetex.cgi?\Large \ell[x(t)]) 로 표기한다고 할 때
로 표기한다고 할 때
![$h(t)=\ell[\delta(t)]$ $h(t)=\ell[\delta(t)]$](/123/cgi-bin/mimetex.cgi?\Large h(t)=\ell[\delta(t)]) 로 나타낸다)
로 나타낸다)
(이걸
일반적 입력 ) 에 대한 선형시스템의 출력
에 대한 선형시스템의 출력
먼저 입력을 적분식으로 바꾸어 쓴다.
=\int_{-\infty}^{\infty}x(\tau)\delta(t-\tau)d\tau)
시스템의 출력 식 ![$y(t)=\ell[x(t)]$ $y(t)=\ell[x(t)]$](/123/cgi-bin/mimetex.cgi?\Large y(t)=\ell[x(t)]) 에 대입한다.
에 대입한다.
![$y(t)=\ell[x(t)]=\ell\left[ \int_{-\infty}^{\infty} x(\tau) \delta(t-\tau) d\tau \right] = \int_{-\infty}^{\infty} x(\tau)\ell[\delta(t-\tau)]d\tau$ $y(t)=\ell[x(t)]=\ell\left[ \int_{-\infty}^{\infty} x(\tau) \delta(t-\tau) d\tau \right] = \int_{-\infty}^{\infty} x(\tau)\ell[\delta(t-\tau)]d\tau$](/123/cgi-bin/mimetex.cgi?\Large y(t)=\ell[x(t)]=\ell\left[ \int_{-\infty}^{\infty} x(\tau) \delta(t-\tau) d\tau \right] = \int_{-\infty}^{\infty} x(\tau)\ell[\delta(t-\tau)]d\tau)
(적분,integration과  은 다 선형성,linearity이 있으므로(i.e. 선형연산자,linear_operator이므로)
은 다 선형성,linearity이 있으므로(i.e. 선형연산자,linear_operator이므로)  이 저렇게 들어갈 수 있다 or 적분연산이 나올 수 있다)
이 저렇게 들어갈 수 있다 or 적분연산이 나올 수 있다)
여기서,![$\ell[\delta(t-\tau)]$ $\ell[\delta(t-\tau)]$](/123/cgi-bin/mimetex.cgi?\Large \ell[\delta(t-\tau)]) 는 지연된 임펄스에 대한 시스템 출력이므로, 시불변에 의해
는 지연된 임펄스에 대한 시스템 출력이므로, 시불변에 의해 ![$\ell[\delta(t-\tau)]=h(t-\tau)$ $\ell[\delta(t-\tau)]=h(t-\tau)$](/123/cgi-bin/mimetex.cgi?\Large \ell[\delta(t-\tau)]=h(t-\tau)) 이다. 이것을 대입하면 시스템 출력:
이다. 이것을 대입하면 시스템 출력:
=\int_{-\infty}^{\infty} x(\tau)h(t-\tau)d\tau)
이 적분,integration을 ) 와
와 ) 의 합성곱,convolution이라 부르며, 간단히 아래와 같이 연산자
의 합성곱,convolution이라 부르며, 간단히 아래와 같이 연산자 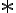 를 써서 나타낸다.
를 써서 나타낸다.
=x(t)*h(t))
정리하면 LTI system에서 임의의 입력,input에 대한 출력,output은, (모든 입력을 일일이 집어넣어 볼 필요 없이,)
임펄스응답만 알고 있다면 입력과의 convolution 적분으로 알아낼 수 있다.
먼저 입력을 적분식으로 바꾸어 쓴다.
여기서,
임펄스응답만 알고 있다면 입력과의 convolution 적분으로 알아낼 수 있다.
convolution의 성질
(14:10)
기호: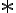
성질:
(14:10)
기호:
성질:
- 교환성 (교환법칙,commutativity)
- 분배성 (분배법칙,distributivity)
- 결합성 (결합법칙,associativity)
- 추이성(shift property) (22:30)
일 때,
(하나를 delay한 것의 convolution은 convolution의 delay와 같다) (convolution은 시불변이다. i.e. convolution operator는 time invariant.)
- impulse와의 convolution (동영상 2.-2 '컨볼루션 적분')
(impulse는 convolution operator의 항등원,identity_element이다)
(- 좀 찾아보니 엄밀한 건 아니고 '항등원 역할을 한다' 정도? chk. impulse convolution identity.element )
impulse convolution identity.element )
- 폭(width):
의 폭이
이고
의 폭이
라면
의 폭은
- 인과성,causality과 관련하여
인과적 신호 // causal_signal ?
if
인과적 시스템의 임펄스 응답 // impulse response of causal_system ?
CHK ¶
어떤 시스템,system의 impulse response는 impulse_function(curr. 디랙_델타함수,Dirac_delta_function) ) 을 그 system에 입력했을 때 나오는 출력?
을 그 system에 입력했을 때 나오는 출력?
중요하므로 그냥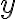 뿐만 아니라
뿐만 아니라 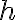 라는 별도의 표기 문자가 있는?
라는 별도의 표기 문자가 있는?
중요하므로 그냥
(이하 여러 언급들, chk)
impulse response를 알면 임의의 입력에 대한 출력을 알 수 있다.
impulse response가 시스템,system에 관해 어떤 입력이 들어갔을 때 어떤 출력이 나오는지에 대해 모든 것을 알고 있다.
impulse response를 아는 것은 시스템을 아는 것이다.
system에 대한 얘기를 impulse response에 대한 얘기로 환원할 수 있다.
라플라스_변환,Laplace_transform
전달함수,transfer_function
이것(unit impulse response)의 라플라스 변환은 시스템의 전달함수 H(s).
transfer function of system = H(s) = Laplace transform { unit impulse response }.
전달함수,transfer_function
이것(unit impulse response)의 라플라스 변환은 시스템의 전달함수 H(s).
transfer function of system = H(s) = Laplace transform { unit impulse response }.
AKA unit sample response[1]
Up: 응답,response

