합성곱, 컨볼루션, 콘볼루션
이거 신시의 (신호,signal의?) convolution과 CNN의 (이미지,image의?) convolution을 별도의 page로 나누는 게 좋을텐데. 핵심 idea는 일치하나 둘은 너무도 달라서. pagename TBD ... image_convolution?
NN > CNN 의 convolution은
{
이미지,image를 주로? 항상? 다루며
용어들은 대략
stride { 번역들: 보폭, }
kernel ~= filter ... 필터,filter > image_filter
flatten
padding
featuring
feature_map
채널,channel - 역시 통신의 채널과는 좀 다른
pooling - max pooling, average pooling, stochastic pooling, ... 최대 풀링 / 평균 풀링 / 확률 풀링 ...
...
NN > CNN 의 convolution은
{
이미지,image를 주로? 항상? 다루며
용어들은 대략
stride { 번역들: 보폭, }
kernel ~= filter ... 필터,filter > image_filter
flatten
padding
featuring
feature_map
채널,channel - 역시 통신의 채널과는 좀 다른
pooling - max pooling, average pooling, stochastic pooling, ... 최대 풀링 / 평균 풀링 / 확률 풀링 ...
...
종류는
LeNet
GoogLeNet
AlexNet
VGGNet
...
}
LeNet
GoogLeNet
AlexNet
VGGNet
...
}
Sub:
이산 discrete_convolution ... 이산성,discreteness // rel? : 코시_곱,Cauchy_product
연속 continous_convolution ... 연속성,continuity
이산 discrete_convolution ... 이산성,discreteness // rel? : 코시_곱,Cauchy_product
연속 continous_convolution ... 연속성,continuity
디리클레 곱 Dirichlet_product  dirichlet.product
dirichlet.product
디리클레 합성곱 Dirichlet_convolution dirichlet.convolution
dirichlet.convolution
같은거? 그럼 pagename?
디리클레 합성곱 Dirichlet_convolution
같은거? 그럼 pagename?
수학백과 '5. 이산 합성곱' 분류에 의하면
정수 수열 두 개 a,b에 대해
이런? chk
정수 수열 두 개 a,b에 대해
이런? chk
2023-03-19
discrete_convolution
continuous_convolution
을 sub로 할까?
continuous_convolution
을 sub로 할까?
각각 syn.이
= discrete-time_convolution
= continuous-time_convolution
인지 chk
= discrete-time_convolution
= continuous-time_convolution
인지 chk
암튼 discrete convolution은 다음 무한합이며 // infinite_sum
![$x[n]=\cdots+x[-2]\delta[n+2]+x[-1]\delta[n+1]+x[0]\delta[n]+x[1]\delta[n-1]+\cdots$ $x[n]=\cdots+x[-2]\delta[n+2]+x[-1]\delta[n+1]+x[0]\delta[n]+x[1]\delta[n-1]+\cdots$](/123/cgi-bin/mimetex.cgi?\Large x[n]=\cdots+x[-2]\delta[n+2]+x[-1]\delta[n+1]+x[0]\delta[n]+x[1]\delta[n-1]+\cdots)
![$x[n]=\sum_{k=-\infty}^{\infty}x[k]\delta[n-k]$ $x[n]=\sum_{k=-\infty}^{\infty}x[k]\delta[n-k]$](/123/cgi-bin/mimetex.cgi?\Large x[n]=\sum_{k=-\infty}^{\infty}x[k]\delta[n-k])
여기서
![$x[k]$ $x[k]$](/123/cgi-bin/mimetex.cgi?\Large x[k]) : coefficients
: coefficients
![$\delta[n-k]$ $\delta[n-k]$](/123/cgi-bin/mimetex.cgi?\Large \delta[n-k]) : basic signals
: basic signals
이다. 즉 signal을 basic signals의 가중합,weighted_sum으로 나타낼 수 있다.
이것을 sifting property of the unit sample이라 한다.
이것을 sifting property of the unit sample이라 한다.
특히 DT LTI system의 특성상, 출력(응답,response)을 구할 때 위 식의 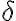 를
를 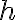 로 바꾼 것과 같다.
로 바꾼 것과 같다.
![$y[n]=\sum_{k=-\infty}^{\infty}x[k]h[n-k]$ $y[n]=\sum_{k=-\infty}^{\infty}x[k]h[n-k]$](/123/cgi-bin/mimetex.cgi?\Large y[n]=\sum_{k=-\infty}^{\infty}x[k]h[n-k])
같은 식을 convolution operator로 표기하면
![$y[n]=x[n]*h[n]$ $y[n]=x[n]*h[n]$](/123/cgi-bin/mimetex.cgi?\Large y[n]=x[n]*h[n])
이다.
다시 말해
ex 1. ![$h[n]=\delta[n]$ $h[n]=\delta[n]$](/123/cgi-bin/mimetex.cgi?\Large h[n]=\delta[n]) 이면
이면
![$y[n]=x[n]*\delta[n]=\sum x[k]\delta[n-k]=x[n]$ $y[n]=x[n]*\delta[n]=\sum x[k]\delta[n-k]=x[n]$](/123/cgi-bin/mimetex.cgi?\Large y[n]=x[n]*\delta[n]=\sum x[k]\delta[n-k]=x[n]) - identity system.
- identity system.
ex 2. ![$h[n]=\delta[n-n_0]$ $h[n]=\delta[n-n_0]$](/123/cgi-bin/mimetex.cgi?\Large h[n]=\delta[n-n_0]) 이면
이면
![$y[n]=x[n]*\delta[n-n_0]=\sum x[k]\delta[n-n_0-k] = x[n-n_0]$ $y[n]=x[n]*\delta[n-n_0]=\sum x[k]\delta[n-n_0-k] = x[n-n_0]$](/123/cgi-bin/mimetex.cgi?\Large y[n]=x[n]*\delta[n-n_0]=\sum x[k]\delta[n-n_0-k] = x[n-n_0]) - a shift.
- a shift.
// via 조준호 https://youtu.be/75y0U5JARCc
정의: ,g(t)) 의 convolution은
의 convolution은
(t):=\int_0^t f(\tau)g(t-\tau)d\tau)
정의: If  and
and 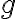 are defined on
are defined on ,) then the convolution
then the convolution 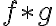 of
of  with
with 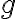 is the function defined by
is the function defined by
(t)=\int_0^t f(t-\tau)g(\tau)d\tau)
for 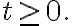
(O'Neil AEM Def. 3.6)
(O'Neil AEM Def. 3.6)
The Convolution Theorem:
![$\mathcal{L}[f\ast g]=\mathcal{L}[f]\mathcal{L}[g]$ $\mathcal{L}[f\ast g]=\mathcal{L}[f]\mathcal{L}[g]$](/123/cgi-bin/mimetex.cgi?\Large \mathcal{L}[f\ast g]=\mathcal{L}[f]\mathcal{L}[g])
Equivalently,
=F(s)G(s)$ $\mathcal{L}[f\ast g](s)=F(s)G(s)$](/123/cgi-bin/mimetex.cgi?\Large \mathcal{L}[f\ast g](s)=F(s)G(s))
The inverse transform version of the convolution theorem:
![$\mathcal{L}^{-1}[FG]=f\ast g$ $\mathcal{L}^{-1}[FG]=f\ast g$](/123/cgi-bin/mimetex.cgi?\Large \mathcal{L}^{-1}[FG]=f\ast g)
(Thm 3.5-)
TBW:
(생각)
convolution은 하나를 fix하고 다른 하나를 move하게 되는데,
commutative property (교환법칙,commutativity) 때문에,
어떤 것을 fix하고 어떤 것을 move할지 잘 정하면 계산이 간단해질 듯?
}
이산함수의 합성곱 이산합성곱
합성곱의 성질 properties
{합성곱의 성질 properties
(생각)
convolution은 하나를 fix하고 다른 하나를 move하게 되는데,
commutative property (교환법칙,commutativity) 때문에,
어떤 것을 fix하고 어떤 것을 move할지 잘 정하면 계산이 간단해질 듯?
}
1. mathworld 요약 (merge later) ¶
함수 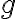 가 shift해서 다른 함수
가 shift해서 다른 함수  위에 얼마나 겹쳤는지(overlap)를 나타내는 적분?
위에 얼마나 겹쳤는지(overlap)를 나타내는 적분?
동사형은 convolve인가 보다... Wolfram language 함수이름이 Convolve. Convolute는 아니고?
추상적으로, 유한한 범위,range ![$[0,t]$ $[0,t]$](/123/cgi-bin/mimetex.cgi?\Large [0,t]) 위로(over) 두 함수
위로(over) 두 함수  의 합성곱은
의 합성곱은
\equiv\int_0^t f(\tau)g(t-\tau)d\tau$ $[f*g](t)\equiv\int_0^t f(\tau)g(t-\tau)d\tau$](/123/cgi-bin/mimetex.cgi?\Large [f*g](t)\equiv\int_0^t f(\tau)g(t-\tau)d\tau)
그런데 무한한 범위에서 구할 경우가 많은데(??) (원문: Convolution is more often taken over an infinite range,)
g(t-\tau)d\tau=\int_{-\infty}^{\infty}g(\tau)f(t-\tau)d\tau)
이하생략.
2. Ref ¶
컨볼루션의 일반적인 정의 https://freshrimpsushi.github.io/posts/generalized-definition-of-convolution/
컨볼루션(합성곱)의 정의 https://freshrimpsushi.github.io/posts/definition-of-convolution/
컨볼루션의 성질 https://freshrimpsushi.github.io/posts/properties-of-convolution/
다변수 함수의 컨볼루션 https://freshrimpsushi.github.io/posts/convolution-of-multi-variable-function/
컨볼루션(합성곱)의 정의 https://freshrimpsushi.github.io/posts/definition-of-convolution/
컨볼루션의 성질 https://freshrimpsushi.github.io/posts/properties-of-convolution/
다변수 함수의 컨볼루션 https://freshrimpsushi.github.io/posts/convolution-of-multi-variable-function/
디리클레_합성곱 Dirichlet_convolution
{
디리클레 합성곱 (Dirichlet Convolution) https://gratus907.com/43
산술 함수의 디리클레 곱 https://freshrimpsushi.github.io/posts/dirichlet-product-of-arithmetical-function/
일반화된 디리클레 곱 https://freshrimpsushi.github.io/posts/generalized-convolution/
{
디리클레 합성곱 (Dirichlet Convolution) https://gratus907.com/43
산술 함수의 디리클레 곱 https://freshrimpsushi.github.io/posts/dirichlet-product-of-arithmetical-function/
일반화된 디리클레 곱 https://freshrimpsushi.github.io/posts/generalized-convolution/
3. Links ko; tmp ¶
https://blog.naver.com/sallygarden_ee/221291514981 (for intuition)
푸리에_변환,Fourier_transform과 합성곱의 관계: convolution_theorem ?  convolution.theorem
convolution.theorem
https://supermemi.tistory.com/105?category=837542
https://supermemi.tistory.com/105?category=837542
4. Links en ¶
Intuitive Guide to Convolution: Convolution is fancy multiplication.
https://betterexplained.com/articles/intuitive-convolution/
저기 맨 위의 정의는
(t)=\int_{-\infty}^{\infty}f(\tau)g(t-\tau)d\tau)
But what is a convolution? (3Blue1Brown)
https://www.youtube.com/watch?v=KuXjwB4LzSA
{
discrete convolution? 수열,sequence의 convolution?
두 수열,\,(b_i)) 의 convolution은
의 convolution은
_n =\sum_{i,j; i+j=n} (a_i \cdot b_j))
) (6은 주사위의 경우)
(6은 주사위의 경우)
즉 대충 곱셈표에서 대각선 ↙ 방향의 값들을 더한 것
https://betterexplained.com/articles/intuitive-convolution/
저기 맨 위의 정의는
https://www.youtube.com/watch?v=KuXjwB4LzSA
{
discrete convolution? 수열,sequence의 convolution?
두 수열
다른 예.
(1,2,3)*(4,5,6)은,
(1,2,3)은 그래로 두고
(4,5,6)은 뒤집어서 (6,5,4)로 하여 한 칸씩 오른쪽으로 이동하면서 위아래 항목들을 곱하여 더한... ('pairwise product') 다음과 같이.
(1,2,3)*(4,5,6)은,
(1,2,3)은 그래로 두고
(4,5,6)은 뒤집어서 (6,5,4)로 하여 한 칸씩 오른쪽으로 이동하면서 위아래 항목들을 곱하여 더한... ('pairwise product') 다음과 같이.
1 2 3
6 5 4 -> 1·4=4
1 2 3
6 5 4 -> 1·5+2·4=13
1 2 3
6 5 4 -> 1·6+2·5+3·4=28
1 2 3
6 5 4 -> 2·6+3·5=27
1 2 3
6 5 4 -> 3·6=18
그래서 결과는 (4,13,28,27,18)이다.이미지,image 이미지처리,image_processing에 있어서 픽셀,pixel 배열,array(비트맵,bitmap?)을
이런 array(? 암튼 3×3 grid of values)와 convolve? convolute? (정확한 동사형이 뭐지?) 하면
흐릿하게 / blur(번역? and pagename? 블러,blur? blur )하는 결과가 나온다.
blur )하는 결과가 나온다.
| ⅑ | ⅑ | ⅑ |
| ⅑ | ⅑ | ⅑ |
| ⅑ | ⅑ | ⅑ |
흐릿하게 / blur(번역? and pagename? 블러,blur?
그리고 저 분포가 저렇게 uniform하지 않고 가운데가 종 모양으로 볼록한 가우스 분포 형태를 띠면 그게 바로 Gaussian_blur.
14:30
np.convolve보다 scipy.signal.fftconvolve가 1000배정도 빠르다.
fftconvolve란? ...MKLINK fast_Fourier_transform(curr. 푸리에_변환,Fourier_transform#s-8)
\ast(4,5,6)=(4,13,28,27,18))
(4+5x+6x^2)=4+13x+28x^2+27x^3+18x^4)
(↙방향 대각선에 같은 degree의 항들)
대충... 계수,coefficient를 가지고 다항식,polynomial으로 만들면 convolution이 다항식의 곱셈과 비슷하다는 ??? chk
}
np.convolve보다 scipy.signal.fftconvolve가 1000배정도 빠르다.
fftconvolve란? ...MKLINK fast_Fourier_transform(curr. 푸리에_변환,Fourier_transform#s-8)
| | |||
| | |||
| |
대충... 계수,coefficient를 가지고 다항식,polynomial으로 만들면 convolution이 다항식의 곱셈과 비슷하다는 ??? chk
}
5. convolution vs cross-correlation ¶
(CNN,convolutional_neural_network에서 image가 input일 때에 대한 설명임)
합성곱,convolution과 상호상관,cross-correlation { Up: 상관,correlation }의 차이는 다음을 참조.
https://youtu.be/Lakz2MoHy6o?t=168
대충 적자면 커널,kernel(pagnename filter_kernel?)을 그대로 적용한게 cross-correlation, fliter를 뒤집어 적용한게 convolution.
여담이지만 저 동영상에선 convolution: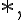 cross-corr:
cross-corr: 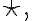 행렬의 180도 회전: rot180 이런 표현을 쓰네.
행렬의 180도 회전: rot180 이런 표현을 쓰네.
합성곱,convolution과 상호상관,cross-correlation { Up: 상관,correlation }의 차이는 다음을 참조.
https://youtu.be/Lakz2MoHy6o?t=168
대충 적자면 커널,kernel(pagnename filter_kernel?)을 그대로 적용한게 cross-correlation, fliter를 뒤집어 적용한게 convolution.
여담이지만 저 동영상에선 convolution:
8. Etc ¶
Twins:
https://mathworld.wolfram.com/Convolution.html (위에 요약해놓음)
https://artofproblemsolving.com/wiki/index.php/Convolution
https://mathworld.wolfram.com/Convolution.html (위에 요약해놓음)
https://artofproblemsolving.com/wiki/index.php/Convolution
![[https]](/123/imgs/https.png) 머신러닝 용어집: 컨볼루션(convolution)
머신러닝 용어집: 컨볼루션(convolution)https://developers.google.com/machine-learning/glossary?hl=ko#convolution
바로 밑에 이어짐: convolutional_filter convolutional_layer convolutional_neural_network (CNN; curr see 신경망,neural_network#s-2) convolutional_operation

