AKA 정전용량, 커패시턴스, 캐패시턴스
기호 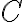
단위 F (farad)
축전기,capacitor에 충전이 완료된 후,
축전기에 쌓인 전하량(전하,electric_charge 양, Q, q)을
축전기 양 끝의 전위차(전위,electric_potential 차이,difference ΔV, 전압,voltage)로 나눈 물리량.
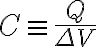
커패시터(축전기,capacitor)에 축적되는 전하량(Q)은 전압(V)이 높을수록, 커패시턴스가 클수록 많이 축적된다.
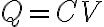

여기서,
같은 뜻의 다른 표현은
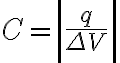 ... source? q, C, ΔV 모두 양수라는데?
... source? q, C, ΔV 모두 양수라는데?
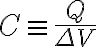
1 F ≡ 1 C/V
저장되는 에너지는 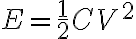 CHK
CHK
단위 F (farad)
1F = 1C/V
(Q=CV, C=Q/V 에서 1F=1C/V)
매우 큰 단위라서 μF, nF, pF가 쓰인다.
정의:(Q=CV, C=Q/V 에서 1F=1C/V)
매우 큰 단위라서 μF, nF, pF가 쓰인다.
축전기,capacitor에 충전이 완료된 후,
축전기에 쌓인 전하량(전하,electric_charge 양, Q, q)을
축전기 양 끝의 전위차(전위,electric_potential 차이,difference ΔV, 전압,voltage)로 나눈 물리량.
같은 뜻의 다른 표현은
1 F ≡ 1 C/V
1. tmp 1 ¶
커패시터에 축적되는 전하 q는

전류는
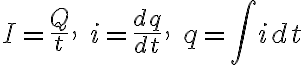
대입하면
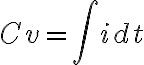
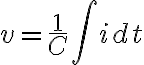
따라서 capacitor 양단 전위차는 전류를 적분한 형태. 그리고 t에 대해 미분하면
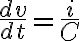
i에 대해 정리하면
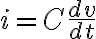
L, C, v, i 표로 만들면
| L(inductance) | C(capacitance) | |
| voltage(v) | ||
| current(i) |
2. 평행판 축전기의 전기용량 ¶
평행판 축전기 정전용량(=전기용량)은, 유전율이 클 수록(분극,polarization 정도가 심해질수록), 판 면적(S)이 넓을수록, 판 사이의 간격이 좁아질수록 커진다.
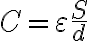
여기서
또는
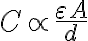
또는
평행판 축전기의 전기 용량 유도법
from 二友출판사 기초물리학:
평행판 축전기의 전기용량 유도
면적 A인 두 도체판이 d만큼 떨어져 있고 각각 +Q, -Q로 대전되어 전하밀도

이고 가장자리 효과를 무시하면 도체판 사이 전기장은
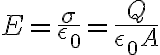
전위차는
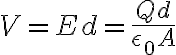
따라서 전기용량은
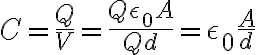
유전체,dielectric를 삽입한 후의 전기용량은
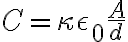
3. 고립된 전도체 구의 전기용량 ¶
from 二友출판사 기초물리학:
반지름 R인 구의 전기용량 계산법.
구에 전하 Q가 대전되면 무한 원점에서의 전위는 0이고 구의 전위는 kQ/R이므로
전위차는 V=kQ/R
따라서

전위차는 V=kQ/R
따라서

