전기장,electric_field + 자기장,magnetic_field
둘을 합쳐 전자기장이라고 함. - ? 둘의 벡터합이 전자기장 아닌가?
일반적으로 전기장과 자기장은 완전히 분리되지 않기 때문에 전자기장이라고 함 (두산백과 전기장)
둘을 합쳐 전자기장이라고 함. - ? 둘의 벡터합이 전자기장 아닌가?
벡터 합이 전자기장인지 아님 두 장을 통틀어 전자기장으로 부르는 것인지...?? chk
사실 나뉠 수가 없으므로(? 따로따로 존재하는 것이 아니므로??), 입자성vs파동성 처럼 같은 것의 두 가지 표현인 것인가?일반적으로 전기장과 자기장은 완전히 분리되지 않기 때문에 전자기장이라고 함 (두산백과 전기장)
q: 전자기파,electromagnetic_wave와의 관계는?
전기장과 자기장의 벡터곱은 포인팅_벡터,Poynting_vector.
| Electric | E | 전기장세기,electric_field_intensity | V/m |
| Electric | D | 전속밀도,electric_flux_density AKA 전기변위장,electric_displacement_field | C/m2 |
| Magnetic | B | 자속밀도,magnetic_flux_density | T |
| Magnetic | H | 자기장세기,magnetic_field_intensity | A/m |
flux density : 단위의 분모가 면적 m2
field intensity : 단위의 분모가 길이 m
Table (CHK later)field intensity : 단위의 분모가 길이 m
| 선속밀도 | 세기 | |
| 전기장 | 전속밀도 D | 전기장의 세기 E |
| 자기장 | 자속밀도 B | 자기장의 세기 H |
1. 네가지 장 ¶
은 바로 E, D, B, H
D, E
D=εE
D=ε0E+P
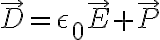
D:D=ε0E+P
P: polarisation density of the electric material 편극밀도
electric displacement 전기변위?
electric displacement field 전기변위장
displacement field 변위장
electric flux density 전속밀도
전기변위장,electric_displacement_field or 전속밀도,electric_flux_density
https://www.britannica.com/science/electric-displacement
D(https://en.wikipedia.org/wiki/Electric_displacement_field)
관련: 변위전류,displacement_current
E:electric displacement field 전기변위장
displacement field 변위장
electric flux density 전속밀도
전기변위장,electric_displacement_field or 전속밀도,electric_flux_density
https://www.britannica.com/science/electric-displacement
D(https://en.wikipedia.org/wiki/Electric_displacement_field)
관련: 변위전류,displacement_current
단위 A/m
}Electric field due to charge 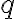 in free space
in free space
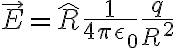
Magnetic field due to current  in free space
in free space
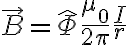
(Ulaby p43 summary)
3. 에너지 밀도 ¶
단위는 J/m3
자기장의 에너지 밀도는
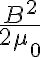
전기장의 에너지 밀도는
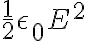
똑같이 생겼는데 다만 진공투자율은 분모로 간다
from SNUON https://www.youtube.com/watch?v=B11D2u_goBs
Up: 밀도,density
에너지밀도,energy_density later
4. 전자기장 텐서 electromagnetic tensor ¶
electromagnetic tensor
electromagnetic field tensor - syn?
electromagnetic field tensor - syn?
abbr. EMF (다만 기전력,electromotive_force,emf과 혼동 위험)
https://everything2.com/title/Electromagnetic field
https://ncatlab.org/nlab/show/electromagnetic field
https://ncatlab.org/nlab/show/electromagnetic field

