좌표,coordinate 로 옮길까???
Sub:
orthogonal coordinate system (좌표축이 서로 수직인 좌표계. 직교좌표계라고 번역할 수 있으나 이 때는 rectangular(=Cartesian)하고 혼동하지 말아야 함.)
curvilinear coordinate 곡선좌표계 (curvilinear adj. 곡선으로 이루어진) Curvilinear_coordinates
Curvilinear_coordinates  곡선좌표계 https://mathworld.wolfram.com/CurvilinearCoordinates.html
곡선좌표계 https://mathworld.wolfram.com/CurvilinearCoordinates.html
좌표계변환 or 좌표변환 좌표변환,coordinate_transformation
2D 극좌표계,polar_coordinate_system, 극좌표,polar_coordinate는 어디에 분류?3D 직교좌표계,rectangular_coordinate_system (Cartesian) 좌표계,coordinate_system#s-2.1 (직각)
3D 원통좌표계,cylindrical_coordinate_system 좌표계,coordinate_system#s-2.2
3D 구면좌표계,spherical_coordinate_system 좌표계,coordinate_system#s-2.3 (구)
// 기타: 타원 원통, 포물선 원통, 원뿔, 편장구면, 편원구면, 타원형 (이게 다 뭐람.. from Sadiku)
nonorthogonal coordinate system (힘듦)3D 원통좌표계,cylindrical_coordinate_system 좌표계,coordinate_system#s-2.2
3D 구면좌표계,spherical_coordinate_system 좌표계,coordinate_system#s-2.3 (구)
// 기타: 타원 원통, 포물선 원통, 원뿔, 편장구면, 편원구면, 타원형 (이게 다 뭐람.. from Sadiku)
curvilinear coordinate 곡선좌표계 (curvilinear adj. 곡선으로 이루어진)
좌표계변환 or 좌표변환 좌표변환,coordinate_transformation
Contents
1. basic facts ¶
축,axis.... 이름은 로마자 마지막 글자인
{
r - 원점에서부터 점 P까지의 거리
원점에서 뻗어나감
x축, y축, z축
원점에서 뻗어나감
거리,distance?원점에서 뻗어나감
{
r - 원점에서부터 점 P까지의 거리
2D 좌표일 때: (0, 0)에서부터의 거리
3D 좌표일 때: (0, 0, 0)에서부터의 거리, 구의 반경
ρ3D 좌표일 때: (0, 0, 0)에서부터의 거리, 구의 반경
원점에서 뻗어나감
범위는 )
}
}
각,angle
{
θ (2D 극좌표에서)
φ (3D 원통, 구면 좌표에서)
azimuth, azimuthal angle, 방위각
x축으로부터 시작하여 처음에 y축 방향으로 향함. P의 xy평면 위의 (정사영? 그림자? 발?) 로 향함
{
θ (2D 극좌표에서)
φ (3D 원통, 구면 좌표에서)
azimuth, azimuthal angle, 방위각
x축으로부터 시작하여 처음에 y축 방향으로 향함. P의 xy평면 위의 (정사영? 그림자? 발?) 로 향함
θ (3D 구면 좌표에서)
천정각(zenith angle)
z축으로부터 시작, z축과 P의 위치벡터의 사이 각
천정각(zenith angle)
z축으로부터 시작, z축과 P의 위치벡터의 사이 각
방위각 φ 범위는 )
천정각 θ 범위는![$[0,\pi]$ $[0,\pi]$](/123/cgi-bin/mimetex.cgi?\Large [0,\pi]) (파이를 포함해야 하는 것에 주의)
(파이를 포함해야 하는 것에 주의)
}
천정각 θ 범위는
}
원통좌표계 (ρ, Φ, z)
{
{
}
구좌표계 (r, θ, Φ)
{
r
θ 천정각 zenith angle
Φ
}
{
r
θ 천정각 zenith angle
Φ
}
영단어
axis 축
origin 원점
quadrant 사분면
ordinate 점의 y좌표
x-axis, horizontal axis
y-axis, vertical axis
axes 축들(axis의 복수형)y-axis, vertical axis
origin 원점
quadrant 사분면
quadrant I, quadrant II, quadrant III, quadrant IV
coordinate 좌표ordered pair(순서쌍)로 나타남
abscissa 점의 x좌표ordinate 점의 y좌표
2. 여러 가지 좌표계의 분류 시도 ¶
직교좌표계(rectangular coordinate system)
원통좌표계(cylindrical coordinate system) - cylinderical가 아니다.
구면좌표계(spherical coordinate system)
원통좌표계(cylindrical coordinate system) - cylinderical가 아니다.
구면좌표계(spherical coordinate system)
2D 평면,plane
fork to
2D 직교좌표계
2D 극좌표계
3D 공간,space2D 극좌표계
3D 직교좌표계
3D 극좌표계 - 원통? 원통+구면?
원통좌표계
구면좌표계
3D 극좌표계 - 원통? 원통+구면?
원통좌표계
구면좌표계
| 2D | ordered pair | 사분면,quadrant |
| 3D | ordered triple | 팔분공간,octant |
fork to
2.1. 직교 ¶
직교좌표계,rectangular_coordinate_system
{
기호

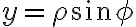
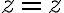
구면좌표계,spherical_coordinate_system(r, θ, φ)에서 직교좌표계로 변환

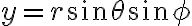
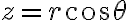
AKA 카테시안 좌표계, 데카르트 좌표계, Cartesian coordinate system, 직각좌표계
Twins: Cartesian_coordinate_system
Cartesian_coordinate_system
}
{
기호
2차원의 경우 )
3차원의 경우)
원통좌표계,cylindrical_coordinate_system(ρ, φ, z)에서 직교좌표계로 변환3차원의 경우
Twins:
}
2.2. 원통 ¶
원통좌표계,cylindrical_coordinate_system
{
평면 극좌표계,polar_coordinate_system에 높이를 더한 것
한 축을 중심으로 대칭성을 갖는 경우에 유용
{
평면 극좌표계,polar_coordinate_system에 높이를 더한 것
한 축을 중심으로 대칭성을 갖는 경우에 유용
기호
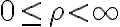

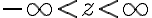

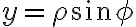
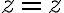
(ρ, φ, z)
)
각 변수의 범위:0 ≤ ρ < ∞
0 ≤ φ < 2π
-∞ < z < ∞
i.e.0 ≤ φ < 2π
-∞ < z < ∞
변환
직교좌표계,rectangular_coordinate_system(x, y, z)에서 원통좌표계로 변환
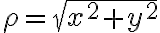

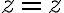
구면좌표계,spherical_coordinate_system(r, θ, φ)에서 원통좌표계로 변환
TBW
right-handle cyclic relations of base unit vectors
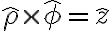
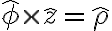
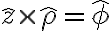
from Ulaby 5e; r을 rho로 바꿈; CHK
2.3. 구면 ¶
기호
θ: 천정각(zenith angle), z축과 P의 위치벡터(r) 사이의 각
φ: 방위각(azimuth), x축으로부터 측정되는 각
(r, θ, φ)
)
r: 거리, (원점에 중심을 둔 구의) 반경(=반지름, radius)θ: 천정각(zenith angle), z축과 P의 위치벡터(r) 사이의 각
φ: 방위각(azimuth), x축으로부터 측정되는 각
0 ≤ r < ∞
0 ≤ θ ≤ π
0 ≤ φ < 2π
0 ≤ θ ≤ π
0 ≤ φ < 2π
θ는 z축부터의 각도이며,
0≤θ≤π 인가? Yes.
0≤φ≤2π ? <2pi.
0≤θ≤π 인가? Yes.
0≤φ≤2π ? <2pi.
θ가 일정하면 conical surface? CHK

| r | radial distance |
| θ | polar angle, zenith angle? |
| φ | azimuthal angle |
zenith=천정, azimuth=방위각.
θ는 위도,latitude
φ는 경도,longitude 와 비교됨??
원통좌표계에서 알아봤듯 다음이 성립함

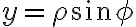
그리고
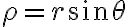
임 CHK
그래서 구면좌표계에서는 ,
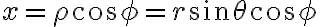
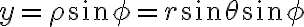
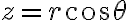
그리고
임 CHK
그래서 구면좌표계에서는 ,
구면좌표계로 변환
(주의: 여기선 r대신 rho 사용)
구면좌표,spherical_coordinate) 를 직교좌표,rectangular_coordinate
를 직교좌표,rectangular_coordinate ) 로 변환
로 변환
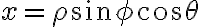
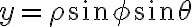
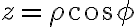
또한
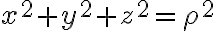
(\rho d\phi)(d\rho)=\rho^2 \sin\phi d\rho d\theta d\phi)
from https://www.youtube.com/watch?v=0Ymw20wa5Ys
구면좌표,spherical_coordinate
구면좌표계의 미소체적/미소부피
from Ulaby 5e 3-2.3
r, theta, phi obey the following right-hand cyclic relations:

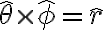
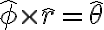
r, theta, phi obey the following right-hand cyclic relations:
AKA 구좌표계
3. basics, 기호 ¶
| Stewart? | Ulaby | |
| rectangular | x y z | x y z |
| cylindrical | ρ φ z | r φ z |
| spherical | r θ φ | R θ φ |
표
거리는 크기, 각은 방향
| rect | 크기 크기 크기 |
| cyli | 크기 방향 크기 |
| sphe | 크기 방향 방향 |
Ulaby 5e에 따르면
ρ : radial distance (in the x-y plane)
φ : azimuth angle (measured from the positive x-axis)
r : range coordinate, 구의 반지름
θ : zenith angle (measured from the positive z-axis; describes a conical surface with its apex(꼭대기/정점) at the origin)
ρ : radial distance (in the x-y plane)
φ : azimuth angle (measured from the positive x-axis)
r : range coordinate, 구의 반지름
θ : zenith angle (measured from the positive z-axis; describes a conical surface with its apex(꼭대기/정점) at the origin)
see  Orthogonal_coordinates#Table_of_orthogonal_coordinates
Orthogonal_coordinates#Table_of_orthogonal_coordinates
 scale.factor coordinate
scale.factor coordinate
scale factor는
근데 주의!! 가운데 단 하나만 다른 (r -> rho)
것도 있는데, 이건 또 뭔지... src: 전기자기학04.pdf
{
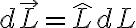
 (직각)
(직각)
 (원통)
(원통)
 (구)
(구)
// 이 파일이 좀 ... 표기가(문자선택이)... 그런듯 2행 1열 r이 rho의 오타인지도 불확실
x y z
r φ z
r θ φ ????
}
CHK
scale factor는
| h1 | h2 | h3 | |
| rect | 1 | 1 | 1 |
| cyli | 1 | r | 1 |
| sphe | 1 | r | rsinθ |
| h1 | h2 | h3 | |
| rect | 1 | 1 | 1 |
| cyli | 1 | ρ | 1 |
| sphe | 1 | r | rsinθ |
{
x y z
r φ z
r θ φ ????
}
CHK
델,del,나블라,nabla#s-2#(여러 좌표계에서) 에도 같은 내용 있음
5. 2차원 직교좌표계 (x, y) ¶
가로축 = 횡축 = abscissa = horizon axis = x axis
세로축 = 종축 = ordinate = vertical axis = y axis
세로축 = 종축 = ordinate = vertical axis = y axis
10.2.1. 직교 ↔ 원통 변환 ¶
3:3 이 아니라 2:2 mapping이다.
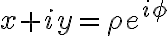
바로 아래 unit vector 표기 생략되어있음
...........이것들은 복잡하므로 내적표를 만든다.........
| · | |||
코 싸 마싸 코
CLEAN
{
(x, y, z)
(ρ, φ, z)
{
(x, y, z)
(ρ, φ, z)
z는 그대로다. 2:2 mapping이다..
A = x+jy = ρejφ
로 변환할 수 있다 카더라....인지 chk
좌표 변환에 쓰이는 벡터 내적 표| · | x | y | z |
| cos | sin | 0 | |
| -sin | cos | 0 | |
| z | 0 | 0 | 1 |
? CHK
}11.1. 직각좌표계에서는 ¶
미소길이/미소변위 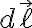 (l: length)은 디퍼렌셜(스칼라)와 단위벡터의 곱의 합으로 나타남
(l: length)은 디퍼렌셜(스칼라)와 단위벡터의 곱의 합으로 나타남
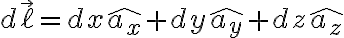
미소면적 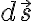 (s: surface)은, 어느 평면에 평행하게 있느냐에 따라
(s: surface)은, 어느 평면에 평행하게 있느냐에 따라
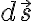
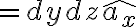 (yz평면에 평행할 경우)
(yz평면에 평행할 경우)
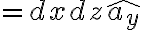 (xz평면에 평행하고, 법선이 y축과 평행)
(xz평면에 평행하고, 법선이 y축과 평행)
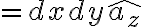
normal vector 방향은 체적에서 멀어지는 방향으로.
이렇게 법선단위벡터와 스칼라 두개씩의 결합으로 표현 가능
미소체적 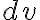 (v: volume) 는 벡터가 아니며
(v: volume) 는 벡터가 아니며
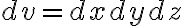
11.4. and ¶
참고로 미소면적은 미소면적크기(스칼라) 곱하기 법선벡터
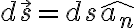
면적 S가 벡터장,vector_field  속에 있을 때
속에 있을 때
면적 S를 통한 의 면적분,surface_integral or 선속,flux
의 면적분,surface_integral or 선속,flux
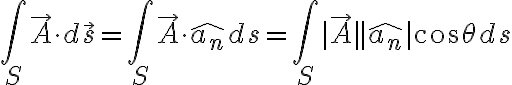
단위벡터의 길이는 1이므로
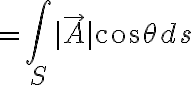
위의 내용은 S가 개곡면일 때 개곡면에 대한 면적분이고,
폐곡면이면..
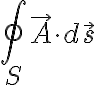 : S를 통해 나가는 순 선속 (net flux)
: S를 통해 나가는 순 선속 (net flux)
Q: 선속은 폐곡면의 면적분에서만 정의되나?
면적 S를 통한
폐곡면이면..


![[https]](/123/imgs/https.png)
![[http]](/123/imgs/http.png)
