QQQ
잰다(measure) = 측정(measurement)한다 = 크기(size)를 부여한다 ?
잰다(measure) = 측정(measurement)한다 = 크기(size)를 부여한다 ?
MKL
해석학,analysis
측정,measurement
노름,norm
정확도,accuracy
정밀도,precision
재현율,recall
가측성,measurability
가측집합,measurable_set - 가측성을 가진 집합,set? chk
측도론,measure_theory
크기,size
길이,length
시그마대수,sigma-algebra ... 가측집합,measurable_sets을 모아 놓은? chk
측도공간,measure_space - w, rr
{
측도,measure가 부여된 가측공간,measurable_space? chk
해석학,analysis
측정,measurement
노름,norm
정확도,accuracy
정밀도,precision
재현율,recall
가측성,measurability
가측집합,measurable_set - 가측성을 가진 집합,set? chk
측도론,measure_theory
크기,size
길이,length
시그마대수,sigma-algebra ... 가측집합,measurable_sets을 모아 놓은? chk
측도공간,measure_space - w, rr
{
측도,measure가 부여된 가측공간,measurable_space? chk
측도공간 중에서, 전체 측도가 1이면 확률공간,probability_space? chk
metric - 비교 필요 ... //  metric
metric  metric
metric  metric
metric
양,quantity
넓이,area를 구한다는 것이
적분,integration이므로 measure와 밀접
확률,probability
확률론,probability_theory
영,zero vs 널,null / 원점,origin
절대값,absolute_value
양,quantity
넓이,area를 구한다는 것이
적분,integration이므로 measure와 밀접
확률,probability
확률론,probability_theory
영,zero vs 널,null / 원점,origin
절대값,absolute_value
Contents
- 1. F측도 F measure = F score
- 2. F1 측도 F1 measure = F1 score
- 3. Borel measure
- 4. Lebesgue measure
- 5. 완비측도 complete measure
- 6. 셈 측도 counting measure
- 7. 이산측도 discrete measure
- 8. 디랙 측도 Dirac measure
- 9. 절대 연속 측도 absolutely continuous measure
- 10. 불변측도 invariant measure
- 11. cylinder set measure
- 12. 측도추가 ADDHERE
- 13. 측도추가 ADDHERE
2. F1 측도 F1 measure = F1 score ¶
F1 = 2 * (precision * recall) / (precision + recall)
Sources:
Kwak Slides 1 p74
https://www.ibm.com/docs/en/cloud-paks/cp-data/4.6.x?topic=overview-f1-measure
Kwak Slides 1 p74
https://www.ibm.com/docs/en/cloud-paks/cp-data/4.6.x?topic=overview-f1-measure
4. Lebesgue measure ¶
6. 셈 측도 counting measure ¶
셈측도,counting_measure
{ (tmp copy; update local, DONOTMODIFYHERE)
/// from![[https]](/123/imgs/https.png) 수학백과: 측도 30% 쯤 "보기 1"
수학백과: 측도 30% 쯤 "보기 1"
공집합,empty_set이 아닌 집합 에 대해
에 대해
 의 멱집합,power_set을
의 멱집합,power_set을 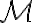 이라 하면 시그마대수,sigma-algebra가 됨.
이라 하면 시그마대수,sigma-algebra가 됨.
부분집합,subset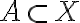 에 대해
에 대해
) 를
를  의 원소의 개수(기수,cardinal_number, 카디널리티,cardinality)로 정의하면,
의 원소의 개수(기수,cardinal_number, 카디널리티,cardinality)로 정의하면,
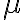 는 측도,measure이며 이를 셈측도(counting measure)라 함.
는 측도,measure이며 이를 셈측도(counting measure)라 함.
{ (tmp copy; update local, DONOTMODIFYHERE)
/// from
![[https]](/123/imgs/https.png) 수학백과: 측도 30% 쯤 "보기 1"
수학백과: 측도 30% 쯤 "보기 1"공집합,empty_set이 아닌 집합
부분집합,subset
https://planetmath.org/CountingMeasure
https://proofwiki.org/wiki/Definition:Counting_Measure
}
9. 절대 연속 측도 absolutely continuous measure ¶
absolutely continuous measure
절대연속측도,absolutely continuous measure
절대연속측도,absolutely continuous measure
11. cylinder set measure ¶
cylinder set measure
"cylinder set measure (or promeasure, or premeasure, or quasi-measure, or CSM)"
MKLcylinder_set
힐베르트_공간,Hilbert_space

