정의가 고유값,eigenvalue과 매우 밀접하므로 같이 참조.
1. ㄷㄱㄱ ¶
정의: 정사각행렬,square_matrix 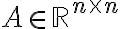 의 고유벡터,eigenvector는,
의 고유벡터,eigenvector는,
어떤 스칼라,scalar 에 대해, 다음 조건을 만족하는 영벡터가 아닌 벡터
에 대해, 다음 조건을 만족하는 영벡터가 아닌 벡터 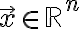 이다.
이다.

이 때  를
를  의 고유값,eigenvalue이라 하며,
의 고유값,eigenvalue이라 하며,
그런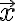 를
를  에 대응하는 고유벡터라고 한다.
에 대응하는 고유벡터라고 한다.
어떤 스칼라,scalar
그런
(원문)
Definition: An eigenvector of a square matrix 𝐴 ∈ ℝ𝑛×𝑛 is a
nonzero vector 𝐱 ∈ ℝ𝑛 such that 𝐴𝐱 = 𝜆𝐱 for some scalar 𝜆
In this case, 𝜆 is called an eigenvalue of 𝐴, and
such an 𝐱 is called an eigenvector corresponding to 𝝀.
Definition: An eigenvector of a square matrix 𝐴 ∈ ℝ𝑛×𝑛 is a
nonzero vector 𝐱 ∈ ℝ𝑛 such that 𝐴𝐱 = 𝜆𝐱 for some scalar 𝜆
In this case, 𝜆 is called an eigenvalue of 𝐴, and
such an 𝐱 is called an eigenvector corresponding to 𝝀.
1.1. 변환,transformation 관점 ¶
선형변환,linear_transformation =A\vec{x}) 를 고려하자.
를 고려하자.
만약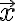 가 고유벡터이면,
가 고유벡터이면, =A\vec{x}=\lambda\vec{x}) 이다.
이다.
즉 출력 벡터가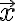 와 같은 방향,direction이면서 길이,length가
와 같은 방향,direction이면서 길이,length가  만큼 규모가 변했다는(scaled) 뜻이다.
만큼 규모가 변했다는(scaled) 뜻이다.
만약
즉 출력 벡터가
(원문)
Consider a linear transformation 𝑇 x = 𝐴x.
If x is an eigenvector, then 𝑇 x = 𝐴x = 𝜆𝐱, which means
the output vector has the same direction as x,
but the length is scaled by a factor of 𝜆.
Consider a linear transformation 𝑇 x = 𝐴x.
If x is an eigenvector, then 𝑇 x = 𝐴x = 𝜆𝐱, which means
the output vector has the same direction as x,
but the length is scaled by a factor of 𝜆.
Ex.
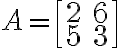 에 대해 고유벡터는
에 대해 고유벡터는 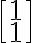 이다. 이유는
이다. 이유는
=A\vec{x}=\begin{bmatrix}2&6\\5&3\end{bmatrix}\begin{bmatrix}1\\1\end{bmatrix}=\begin{bmatrix}8\\8\end{bmatrix}=8\begin{bmatrix}1\\1\end{bmatrix})
이 식에서
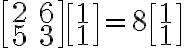 부분은
부분은
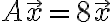 와 동등.
와 동등.
그렇다면 computational advantage가 있다는 것을 알 수 있다. 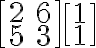 와
와 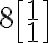 중에 어떤 것을 빨리 계산할 수 있는지는 명백하다.
중에 어떤 것을 빨리 계산할 수 있는지는 명백하다.
2. 나카이 에츠지 ¶
임의의 상수 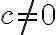 에 대해
에 대해
=\lambda(c\vec{x}))
이므로 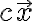 도 고유값
도 고유값  의 고유벡터이다.
의 고유벡터이다.
i.e.
고유벡터에는 상수배에 관해 임의성이 있다.
i.e.
고유벡터에는 상수배에 관해 임의성이 있다.
한 벡터 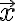 가 서로 다른 고유값
가 서로 다른 고유값 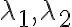 모두의 고유벡터가 될 수 없다.
모두의 고유벡터가 될 수 없다.
pf. 만일 두 고유값의 고유벡터라면
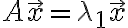
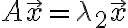
\vec{x})
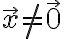 이므로
이므로 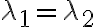 인데, 이것은 다른 고유값이라고 전제한 것에 모순.
인데, 이것은 다른 고유값이라고 전제한 것에 모순.
행렬,matrix이 고유벡터를 가지는지 판정하는 법
어떤 벡터,vector 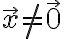 이 고유값
이 고유값  의 고유벡터라면
의 고유벡터라면

\vec{x}=\vec{0})
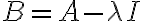 라면
라면
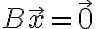
이 연립일차방정식의 해로 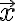 가 결정되며, B가 정칙행렬(가역행렬,invertible_matrix)이라면
가 결정되며, B가 정칙행렬(가역행렬,invertible_matrix)이라면 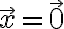 이 되어 고유벡터가 없다.
이 되어 고유벡터가 없다.
고유벡터가 존재하기 위한 필요조건은 detB=0, 즉
=0)
만일 A가

이렇다면,
![$\det\left[ \begin{bmatrix}a&b\\c&d\end{bmatrix} - \lambda\begin{bmatrix}1&0\\0&1\end{bmatrix} \right]$ $\det\left[ \begin{bmatrix}a&b\\c&d\end{bmatrix} - \lambda\begin{bmatrix}1&0\\0&1\end{bmatrix} \right]$](/123/cgi-bin/mimetex.cgi?\Large \det\left[ \begin{bmatrix}a&b\\c&d\end{bmatrix} - \lambda\begin{bmatrix}1&0\\0&1\end{bmatrix} \right])
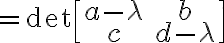
\lambda+(ad-bc))
이런  에 대한 이차방정식,quadratic_equation을 행렬 A의 고유방정식이라 함.
에 대한 이차방정식,quadratic_equation을 행렬 A의 고유방정식이라 함.
(=특성방정식,characteristic_equation?)
고유벡터가 존재하기 위한 필요조건은 detB=0, 즉
(=특성방정식,characteristic_equation?)
행렬 A의 고유방정식이 서로 다른 실수해 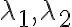 를 가질 때, 서로 일차독립인(see 선형독립,linear_independence) 고유벡터
를 가질 때, 서로 일차독립인(see 선형독립,linear_independence) 고유벡터 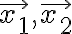 를 가진다.
를 가진다.
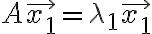
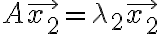
표준기저,standard_basis 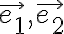 를
를 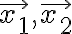 로 옮기는 변환(선형변환,linear_transformation)을 나타내는 행렬을 C라고 하면
로 옮기는 변환(선형변환,linear_transformation)을 나타내는 행렬을 C라고 하면

왼쪽에 C-1을 오른쪽에 C를 곱하면
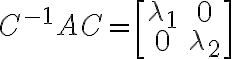
이렇게 대각행렬,diagonal_matrix이 된다.
이렇게, 어떤 정사각행렬 A에 정칙행렬(가역행렬,invertible_matrix) C와 그 역행렬 C-1을 양쪽에 곱해서 대각행렬로 변환시키는 작업을 대각화,diagonalization라고 한다.
QQQ 위 내용 고유값분해,eigendecomposition인가? CHK
4. tmp from MW ¶
사실 두 가지 eigenvectors
left_eigenvector https://mathworld.wolfram.com/LeftEigenvector.html - 행벡터,row_vector
right_eigenvector https://mathworld.wolfram.com/RightEigenvector.html - 열벡터,column_vector
가 있으나 대개의 물리 및 공학 문제에 있어 보통 right eigenvector 하나만을 생각하는 것 만으로 충분하다. 그냥 eigenvector라 하면 right eigenvector를 뜻한다.
left_eigenvector https://mathworld.wolfram.com/LeftEigenvector.html - 행벡터,row_vector
right_eigenvector https://mathworld.wolfram.com/RightEigenvector.html - 열벡터,column_vector
가 있으나 대개의 물리 및 공학 문제에 있어 보통 right eigenvector 하나만을 생각하는 것 만으로 충분하다. 그냥 eigenvector라 하면 right eigenvector를 뜻한다.
Twins:
![[https]](/123/imgs/https.png) 수학백과: 고유벡터
수학백과: 고유벡터
https://everything2.com/title/eigenvector
 eigenvector
eigenvector
https://encyclopediaofmath.org/wiki/Eigen_vector
![[https]](/123/imgs/https.png) 수학백과: 고유벡터
수학백과: 고유벡터https://everything2.com/title/eigenvector
https://encyclopediaofmath.org/wiki/Eigen_vector

