평균을 일반화한 것..?
자연수 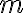 에 대해
에 대해
)
을  의
의 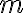 번째 적률(
번째 적률( 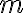 th moment ) 로 정의함.
th moment ) 로 정의함.
첫번째 적률 E(X1)은 평균,mean,average. 기대값,expected_value도? - 대표값,평균값,중앙값,최빈값?
두번째 적률 E(X2)은 분산,variance.
세번째 적률 E(X3)은 왜도,skewness.
네번째 적률 E(X4)은 첨도,kurtosis.
두번째 적률 E(X2)은 분산,variance.
세번째 적률 E(X3)은 왜도,skewness.
네번째 적률 E(X4)은 첨도,kurtosis.
tmp 0 ¶
from http://networksciencebook.com/chapter/2#degree 20%쯤 Box 2.2
Average(mean):
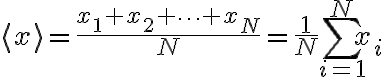
The nth moment:
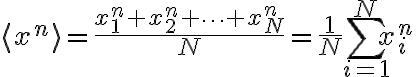
QQQ langle rangle 표기는 network_theory / graph_theory에서 자주 쓰이는듯? 저기선 전체 수를  보다는
보다는 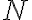 으로 표기하는 경향도 보이는데.
으로 표기하는 경향도 보이는데.
tmp 1 ¶
from https://hsm-edu.tistory.com/756?category=810686 (글 3개) ; chk
물리에서
0차적률 질량,mass
1차적률 질량중심,mass_center
2차적률 관성모멘트,moment_of_inertia
통계학에서
1차적률 평균,mean,average
2차적률 분산,variance
3차적률 왜도,skewness
4차적률 첨도,kurtosis
 차 적률의 정의는, (언급이 없으면 c=0으로 간주)
차 적률의 정의는, (언급이 없으면 c=0으로 간주)
^n f(x)dx)
보다시피,
평균 E(X)는 n=1, c=0인, 1차 적률.
분산 V(X)는 n=2, c=(평균)인, 2차 적률.
물리에서
0차적률 질량,mass
1차적률 질량중심,mass_center
2차적률 관성모멘트,moment_of_inertia
통계학에서
1차적률 평균,mean,average
2차적률 분산,variance
3차적률 왜도,skewness
4차적률 첨도,kurtosis
평균 E(X)는 n=1, c=0인, 1차 적률.
분산 V(X)는 n=2, c=(평균)인, 2차 적률.
Bmks
https://bluehorn07.github.io/mathematics/2021/04/13/momemtum-generating-function.html
https://freshrimpsushi.github.io/posts/moment-generating-function/
https://freshrimpsushi.github.io/posts/moment-generating-function/
tmp from http://blog.naver.com/mykepzzang/220846464280
and Namu so CHK
{
특정 확률분포,probability_distribution의 적률을 생성하는 함수.
적률,moment은 물리의 모멘트,moment에서 가져온 개념.
and Namu so CHK
{
특정 확률분포,probability_distribution의 적률을 생성하는 함수.
적률,moment은 물리의 모멘트,moment에서 가져온 개념.
확률변수의 적률(모멘트).............
확률변수,random_variable 혹은 확률분포의 차 적률 혹은
차 적률 혹은  차 모멘트란, 확률변수를 n번 거듭제곱한 것의 기대값,expected_value.
차 모멘트란, 확률변수를 n번 거듭제곱한 것의 기대값,expected_value.
![$\mu_n=\mathbb{E}[X^n]$ $\mu_n=\mathbb{E}[X^n]$](/123/cgi-bin/mimetex.cgi?\Large \mu_n=\mathbb{E}[X^n])
적률생성함수는 이 적률을 계수로 갖는 급수,series.
![$M_X(t)=\mathbb{E}[e^{tX}]$ $M_X(t)=\mathbb{E}[e^{tX}]$](/123/cgi-bin/mimetex.cgi?\Large M_X(t)=\mathbb{E}[e^{tX}])
만약 위 기대값이 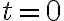 근방에서 수렴한다면, 다음처럼 급수전개가 가능함을 증명할 수 있다고. (다만 확률변수
근방에서 수렴한다면, 다음처럼 급수전개가 가능함을 증명할 수 있다고. (다만 확률변수  가
가 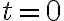 근방에서 적분가능해야 의미가 있음)
근방에서 적분가능해야 의미가 있음)
![$M_X(t) = \mathbb{E}\left[\sum_{k=0}^{\infty} \frac{(tX)^k}{k!}\right] = \sum_{k=0}^{\infty} \frac{t^k}{k!} \mathbb{E}[X^k]$ $M_X(t) = \mathbb{E}\left[\sum_{k=0}^{\infty} \frac{(tX)^k}{k!}\right] = \sum_{k=0}^{\infty} \frac{t^k}{k!} \mathbb{E}[X^k]$](/123/cgi-bin/mimetex.cgi?\Large M_X(t) = \mathbb{E}\left[\sum_{k=0}^{\infty} \frac{(tX)^k}{k!}\right] = \sum_{k=0}^{\infty} \frac{t^k}{k!} \mathbb{E}[X^k])
따라서 테일러_정리,Taylor_theorem에 의해 }(0)) 을 얻을 수 있다 함.
을 얻을 수 있다 함.
확률변수,random_variable 혹은 확률분포의
Sub: 결합적률생성함수 joint mgf 결합적률생성함수,joint_moment_generating_function,joint_MGF
{
결합적률생성함수, joint moment generating function, joint mgf
{
결합적률생성함수, joint moment generating function, joint mgf
from  적률생성함수
적률생성함수
{
확률변수,random_variable 가 다음과 같은 다변수확률변수일 경우,
가 다음과 같은 다변수확률변수일 경우,
)
적률생성함수의 테일러_급수,Taylor_series는 결합적률,joint_moment
![$\mu_{(k_1,k_2,\cdots,k_n)}=\mathbb{E}[X_1^{k_1},X_2^{k_2},\cdots,X_n^{k_n}]$ $\mu_{(k_1,k_2,\cdots,k_n)}=\mathbb{E}[X_1^{k_1},X_2^{k_2},\cdots,X_n^{k_n}]$](/123/cgi-bin/mimetex.cgi?\Large \mu_{(k_1,k_2,\cdots,k_n)}=\mathbb{E}[X_1^{k_1},X_2^{k_2},\cdots,X_n^{k_n}])
을 나타냄.
{
확률변수,random_variable
연속확률분포,continuous_probability_distribution의 경우, mgf는 확률분포함수(확률분포,probability_distribution)의 라플라스_변환,Laplace_transform이라고.
}
}
모멘트,moment와 이름이 같음. QQQ 관계?
일차모멘트=일차적률: 질량중심,mass_center - curr goto 질량,mass#s-7
TODO 아래 내용 질량중심,mass_center, 혹은 first_moment 혹은 moment(모멘트,moment or 적률,moment?) 중 적당한 곳으로 옮기거나 정리.
{
시소(seesaw)에서, 질량,mass이 각각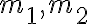 인 물체가 시소 중심으로부터 각각 왼쪽으로
인 물체가 시소 중심으로부터 각각 왼쪽으로 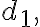 오른쪽으로
오른쪽으로 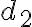 인 거리,distance 인 지점에 있다면 평형을 이루기 위한 필충조건은
인 거리,distance 인 지점에 있다면 평형을 이루기 위한 필충조건은
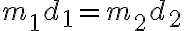
QQQQ증명
TODO 아래 내용 질량중심,mass_center, 혹은 first_moment 혹은 moment(모멘트,moment or 적률,moment?) 중 적당한 곳으로 옮기거나 정리.
{
시소(seesaw)에서, 질량,mass이 각각
점질량이 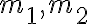 인 물체가 각각 위치
인 물체가 각각 위치 ) 에 있으면 질량중심
에 있으면 질량중심 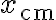 은 위 식에 따라
은 위 식에 따라
=m_2(x_2-x_{\rm cm}))
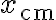 에 대해 정리하면
에 대해 정리하면
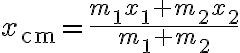
일반적으로  개의 질량
개의 질량 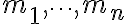 이 각각
이 각각 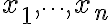 에 놓여 있을 때 질량중심은
에 놓여 있을 때 질량중심은
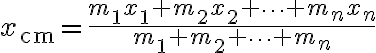
여기서 분자의 식 : 일차능률(first moment)
분모 : 전체 질량
(질량중심) = (일차능률) / (전체 질량)
여기서 분자의 식 : 일차능률(first moment)
분모 : 전체 질량
단위길이당 질량인 밀도,density ) 인 물질이 위치,position
인 물질이 위치,position 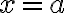 부터
부터 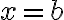 까지 길이,length
까지 길이,length 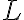 인 곳에 펼쳐져 있을 때,
인 곳에 펼쳐져 있을 때,
밀도가 상수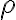 이면, 질량
이면, 질량 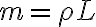 이다.
이다.
밀도가 변하면, 구간,interval![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) 를 같은 크기의
를 같은 크기의  개로 나누어
개로 나누어 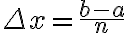 이라 하고, 각 소구간과 그 안의 한 점
이라 하고, 각 소구간과 그 안의 한 점 ![$[x_{i-1},x_i]\ni c_i$ $[x_{i-1},x_i]\ni c_i$](/123/cgi-bin/mimetex.cgi?\Large [x_{i-1},x_i]\ni c_i) 이 있으면
이 있으면
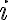 번째 조각의 질량은
번째 조각의 질량은 \Delta x) 이고
이고
이 계의 이산적(?) 일차능률은
![$M_n=[\rho(c_1)\Delta x]c_1+[\rho(c_2)\Delta x]c_2+\cdots+[\rho(c_n)\Delta x]c_n$ $M_n=[\rho(c_1)\Delta x]c_1+[\rho(c_2)\Delta x]c_2+\cdots+[\rho(c_n)\Delta x]c_n$](/123/cgi-bin/mimetex.cgi?\Large M_n=[\rho(c_1)\Delta x]c_1+[\rho(c_2)\Delta x]c_2+\cdots+[\rho(c_n)\Delta x]c_n)
![$=[c_1\rho(c_1)+c_2\rho(c_2)+\cdots+c_n\rho(c_n)]\Delta x$ $=[c_1\rho(c_1)+c_2\rho(c_2)+\cdots+c_n\rho(c_n)]\Delta x$](/123/cgi-bin/mimetex.cgi?\Large =[c_1\rho(c_1)+c_2\rho(c_2)+\cdots+c_n\rho(c_n)]\Delta x)
\Delta x)
연속적(?) 일차능률은 극한을 취하면
\Delta x=\int_a^b x\rho(x)dx)
물체의 질량중심은
dx}{\textstyle\int_a^b \rho(x)dx})
from https://blog.naver.com/dydrogud22/220065026152 chk
밀도가 상수
밀도가 변하면, 구간,interval
이 계의 이산적(?) 일차능률은
Bmks ko ¶
수리통계학에서의 기대값, 평균, 분산, 적률의 정의 https://freshrimpsushi.github.io/posts/expectation-mean-variance-moment/ - 중간쯤에 적률 정의
Up: 통계,statistics


![[https]](/123/imgs/https.png)