tmp bmks ko
테일러 급수의 유도와 의미
https://angeloyeo.github.io/2019/09/02/Taylor_Series.html
어떤 함수를 다항함수,function#s-9.1 (다항식,polynomial, 테일러_다항식,Taylor_polynomial?)로 근사,approximation(curr goto 선형근사,linear_approximation)하는?
https://angeloyeo.github.io/2019/09/02/Taylor_Series.html
어떤 함수를 다항함수,function#s-9.1 (다항식,polynomial, 테일러_다항식,Taylor_polynomial?)로 근사,approximation(curr goto 선형근사,linear_approximation)하는?
1. 정의 ¶
q:한없이 미분가능할 때만 정의?
테일러_정리,Taylor_theorem에 의하면 어떤 조건을 만족하는 함수는 항상 테일러 급수로 나타낼 수 있다. via https://mathworld.wolfram.com/TaylorsTheorem.html
n 대신 k를 쓰면,
}(x_{0})}{k!}(x-x_{0})^{k}})
5.2. 성질 ¶
가 수렴하는 점
들의 집합은 구간이 된다. 이 구간을 수렴구간이라고 부른다.
- 수렴구간의 중심은
이다. 이 때 수렴구간의 길이의 반을 수렴반경이라고 부른다.
(단, 구간의 양 끝점에서는 각각 수렴할 수도 있고 수렴하지 않을 수도 있음)
- 수렴반경공식: 테일러 급수에서
의 계수를
이라고 할 때
- 수렴 구간 내부의 임의의 점에서 함수를 미분하거나 적분한 것은 테일러 급수의 항마다 미분하거나 적분한 것과 동일하다.
5.3. 해석적 ¶
6. 여러 함수의 테일러 전개 ¶
가 성립하므로,
쌍곡선함수,hyperbolic_function의 테일러 전개
이것은,
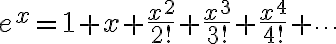
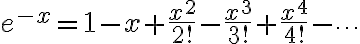
와
)
)
에서 유도 가능.
와
에서 유도 가능.
로그함수,logarithmic_function은 lnx가 아니라 ln(x+1) 테일러 전개가 소개되는데, 이유?
CHK
CHK
Ref. (ko)
![[http]](/123/imgs/http.png) 수학백과: 테일러 급수
수학백과: 테일러 급수
https://freshrimpsushi.github.io/posts/taylor-series-and-maclaurin-series/
 테일러.급수
테일러.급수
![[http]](/123/imgs/http.png) 수학백과: 테일러 급수
수학백과: 테일러 급수https://freshrimpsushi.github.io/posts/taylor-series-and-maclaurin-series/
Ref. (en)
 Taylor_series
Taylor_series
http://mathworld.wolfram.com/TaylorSeries.html
https://encyclopediaofmath.org/wiki/Taylor_series
https://oeis.org/wiki/Taylor_series
https://calculus.subwiki.org/wiki/Taylor_series
https://en.citizendium.org/wiki/Taylor_series
http://mathworld.wolfram.com/TaylorSeries.html
https://encyclopediaofmath.org/wiki/Taylor_series
https://oeis.org/wiki/Taylor_series
https://calculus.subwiki.org/wiki/Taylor_series
https://en.citizendium.org/wiki/Taylor_series

