//chk and 엄밀하게 rewrite
집합,set의 일종.
벡터 하나의 span은 single line. - 직선,line
(종속이 아니고 독립인?) 두 벡터의 span은 plane. - 평면,plane
종속인 벡터는 (basis에?) (추가해봤자) span을 증가시키지 못함.
(종속이 아니고 독립인?) 두 벡터의 span은 plane. - 평면,plane
종속인 벡터는 (basis에?) (추가해봤자) span을 증가시키지 못함.
수식으로 (대충임, 정확한 조건 등 확인 후 추가 필요)
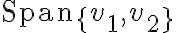 은 평면을
은 평면을
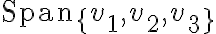 은 공간을
은 공간을
AKA 펼침
AKA spanning, spanning set, 생성집합, spanning subset 모두같은지CHK - 혹시 span(n./v.)/spanning(n.)은 행동이고 span(n.)/spanning set은 그 결과인가?
{
Let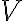 be a vector space and let
be a vector space and let 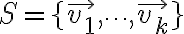 be a subset of
be a subset of 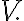 Define the set
Define the set
:=\lbrace a_1\vec{v_1}+\cdots+a_k\vec{v_k} \,:\; a_i\in\mathbb{R},\, i=1,\cdots,k \rbrace.)
Note that \le V.)
If=V,) then we say that
then we say that 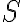 spans
spans 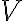 and
and 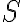 is called a spanning subset of
is called a spanning subset of 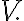
![[https]](/123/imgs/https.png) src
src
AKA spanning, spanning set, 생성집합, spanning subset 모두같은지CHK - 혹시 span(n./v.)/spanning(n.)은 행동이고 span(n.)/spanning set은 그 결과인가?
{
Let
If
![[https]](/123/imgs/https.png) src
src벡터공간 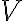 의 모든 벡터를
의 모든 벡터를 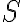 에 있는 벡터들의 일차결합으로 쓸 수 있으면, 즉
에 있는 벡터들의 일차결합으로 쓸 수 있으면, 즉 ) 이면,
이면, 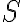 를
를 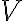 의 생성집합(spanning set)이라 한다. 예를 들면 세 집합
의 생성집합(spanning set)이라 한다. 예를 들면 세 집합
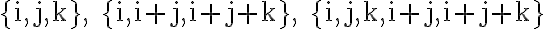
각각이 벡터공간 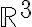 의 생성집합이다. 이 개념을 써서 (책에서 앞서 언급했던) 벡터공간의 기저와 차원을 다음과 같이 정의할 수도 있다.
의 생성집합이다. 이 개념을 써서 (책에서 앞서 언급했던) 벡터공간의 기저와 차원을 다음과 같이 정의할 수도 있다.
(Zill 6e ko p444)
}
}
일단 간단히 두 벡터의 경우만 보면
The span of and
and 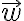 is the set of all their linear combinations.
is the set of all their linear combinations.
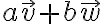
Let  and
and 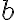 vary over all real numbers:
vary over all real numbers: 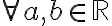
그래서 2D에서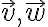 의
의
방향이 같으면 span은 직선.
방향이 다르면 span은 평면 전체. 3D에서는 공간 중에서 한 평면만.
(영벡터는 없는 걸로 가정하는 듯)
이후 내용:
v, w 방향이 같으면 linearly dependent.
v, w 방향이 다르면 linearly independent. (CHK)
"Linearly dependent"
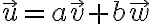 for some values of
for some values of  and
and 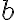
"Linearly independent"
 for all values of
for all values of 
Technical definition of basis:
(https://www.youtube.com/watch?v=k7RM-ot2NWY 중간 쯤)
The span of
그래서 2D에서
방향이 같으면 span은 직선.
방향이 다르면 span은 평면 전체. 3D에서는 공간 중에서 한 평면만.
(영벡터는 없는 걸로 가정하는 듯)
이후 내용:
v, w 방향이 같으면 linearly dependent.
v, w 방향이 다르면 linearly independent. (CHK)
"Linearly dependent"
(https://www.youtube.com/watch?v=k7RM-ot2NWY 중간 쯤)
부분공간,subspace: 벡터공간,vector_space에서 정의된 벡터합과 스칼라곱에 대해 닫혀있는 부분집합
행공간,row_space: 행벡터들의 생성공간
열공간,column_space: 열벡터들의 생성공간
행공간과 열공간은 차원,dimension이 같고, 행렬의 계수,rank와도 동일.
영공간,null_space: Ax=0의 해집합
퇴화차수,nullity: 영공간의 차원
행공간,row_space: 행벡터들의 생성공간
열공간,column_space: 열벡터들의 생성공간
행공간과 열공간은 차원,dimension이 같고, 행렬의 계수,rank와도 동일.
영공간,null_space: Ax=0의 해집합
퇴화차수,nullity: 영공간의 차원
A의 계수 + A의 퇴화차수 = A의행계수(?)
}}
If 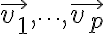 are in
are in 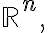 then the set of all linear combinations of
then the set of all linear combinations of 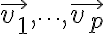 is denoted by
is denoted by
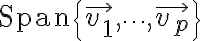
and is called the
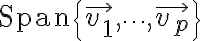 is the collection of all vectors that can be written in the form
is the collection of all vectors that can be written in the form
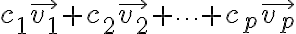
with 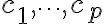 scalars.
scalars.
subset of 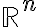 spanned (or generated) by
spanned (or generated) by 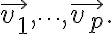
That is, (Lay)
If 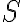 denotes any set of vectors
denotes any set of vectors 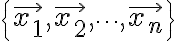 in a vector space
in a vector space 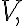 then the set of all linear combinations of the vectors
then the set of all linear combinations of the vectors 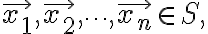
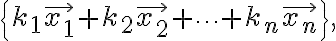
is called the span of the vectors and written
) or
or .)
Span(S) is a subspace of the vector space V.
( 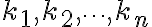 are scalars )
are scalars )
(Zill 7.6 끝부분)
영벡터의 생성은 영벡터 뿐 (당연. 영벡터에 뭐를 곱해도 영벡터이므로)
어떤 생성 집합만으로는 벡터를 유일하게 표현할 수 없을 수 있다. 여기서 나오는 개념이 일차독립=선형독립,linear_independence이다.
성분의 수가 같은 벡터들 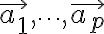 이 주어졌다고 하고, 이들의 선형결합,linear_combination으로 표현되는 모든 벡터들의 집합을 이들 벡터들의 생성공간(span)이라 한다. 생성공간은 그 자체로 벡터공간,vector_space이 됨을 알 수 있다. 만일 주어진 벡터들
이 주어졌다고 하고, 이들의 선형결합,linear_combination으로 표현되는 모든 벡터들의 집합을 이들 벡터들의 생성공간(span)이라 한다. 생성공간은 그 자체로 벡터공간,vector_space이 됨을 알 수 있다. 만일 주어진 벡터들 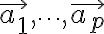 이 선형독립,linear_independence이라면, 이 벡터들은 해당 생성공간의 기저,basis임을 알 수 있다.
이 선형독립,linear_independence이라면, 이 벡터들은 해당 생성공간의 기저,basis임을 알 수 있다.
이 사실은 기저를 다른 방식으로 정의할 수 있게 해 준다. 벡터공간 V에 속한 몇 개의 벡터들로 집합을 만들었다고 하자.
참고로, 성질 (2)가 성립할 때, 그 집합의 벡터들이 벡터공간 V를 생성한다라고 말한다.
이 사실은 기저를 다른 방식으로 정의할 수 있게 해 준다. 벡터공간 V에 속한 몇 개의 벡터들로 집합을 만들었다고 하자.
(1) 이 집합의 벡터들이 선형독립이고,
(2) V에 속한 임의의 벡터는 이 집합의 벡터들의 선형결합으로 나타낼 수 있다면,
이 집합은 V의 기저이다.(2) V에 속한 임의의 벡터는 이 집합의 벡터들의 선형결합으로 나타낼 수 있다면,
참고로, 성질 (2)가 성립할 때, 그 집합의 벡터들이 벡터공간 V를 생성한다라고 말한다.
행렬 A에 대해, 그
이라고 부른다.
이라고 부른다.
행렬 A의 행공간과 열공간의 차원이 같고 rank(A)와 동일하다는 내용 생략. TBW.
행렬 A에 대한 제차연립방정식 Ax=0의 해를 모두 모은 해집합을 A의 영공간,null_space이라 부르며, 이는 벡터공간이다. 또한 영공간의 차원을 A의 퇴화차수,nullity라 한다. 다음 절에서 (A의 계수) + (A의 퇴화차수) = (행렬 A의 행 개수)를 증명할 것이다. (대충 적음)
(Kreyszig 7.4 벡터공간)
rename this page to 선형생성,linear_span or aka(redirect)로 처리?
(주의) 단어 span은 linalg를 벗어나면 의미가 달라질 수 있음.
MW에선 vector space span, WpEn과 nLab에선 linear span이라 하여 구분함.
MathWorld 해당 페이지는 https://mathworld.wolfram.com/Span.html 가 아니라 https://mathworld.wolfram.com/VectorSpaceSpan.html
(https://ncatlab.org/nlab/show/span - 관계,relation를 일반화한 개념) 벡터공간,vector_space이나 module의 span에 대해선 see: https://ncatlab.org/nlab/show/linear span <- linear combinations 페이지로 redir.
MW에선 vector space span, WpEn과 nLab에선 linear span이라 하여 구분함.
MathWorld 해당 페이지는 https://mathworld.wolfram.com/Span.html 가 아니라 https://mathworld.wolfram.com/VectorSpaceSpan.html
(https://ncatlab.org/nlab/show/span - 관계,relation를 일반화한 개념) 벡터공간,vector_space이나 module의 span에 대해선 see: https://ncatlab.org/nlab/show/linear span <- linear combinations 페이지로 redir.


![[http]](/123/imgs/http.png)