Difference between r1.36 and the current
@@ -1,3 +1,4 @@
#noindex
AKA '''전기선속, 전기장 선속,''' 전기다발, 전기장 다발, 전기선다발, flux of the electric fieldNumber of field lines penetrating surface.
@@ -132,5 +133,4 @@
Up:[[선속,flux]]
[[전자기학,electromagnetism]]
AKA 전기선속, 전기장 선속, 전기다발, 전기장 다발, 전기선다발, flux of the electric field
Number of field lines penetrating surface.
기호: Φ, ΦE

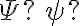 (ysi)
(ysi)
(cf. 전속밀도는 D)
단위:
A: 전속은 전하로부터 나온 것이므로 비례한다. i.e. 전속은 전하에서 발산해 나온다.
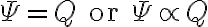
또한 전속은 전속밀도 (전속밀도,electric_flux_density D)를 면적분
from![[http]](/123/imgs/http.png) src ysi 3강 44m
src ysi 3강 44m
see also 가우스_법칙,Gauss_s_law#s-9(ysi) 2020-10-14
(cf. 전속밀도는 D)
V m
N m2
C−1
Q: 단위가 C이라는 데도 있는데 이건 뭐임?N m2
C−1
A: 전속은 전하로부터 나온 것이므로 비례한다. i.e. 전속은 전하에서 발산해 나온다.
from
![[http]](/123/imgs/http.png) src ysi 3강 44m
src ysi 3강 44msee also 가우스_법칙,Gauss_s_law#s-9(ysi) 2020-10-14
전기장 속에서, 전기장에 수직인 가상의 면적에 작용하는 전기력을 나타냄. 전기력선에 수직인 면을 지나가는 전기력선의 개수. (두산백과)
자기장,magnetic_field의 자기선속(자속,magnetic_flux)에 대응.
자기장,magnetic_field의 자기선속(자속,magnetic_flux)에 대응.
전기장(E)이 균일하고, 전기력선에 수직인 면의 넓이가 A이면, 전기력선 다발(전기력선속)은
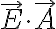
Φ=EA
전기장 다발 ΦE = (전기장이 수직으로 통과하는 면적) × (전기장) = 면 A가 전기장과 수직이면, 전기선속 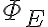 = 전기장 세기
= 전기장 세기 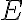 × 전기장에 수직인 면의 면적
× 전기장에 수직인 면의 면적 
면이 전기장과 수직이 아니면, 면 를 통과하는 전기선속
를 통과하는 전기선속 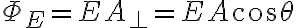
면이 전기장과 수직이 아니면, 면
전기다발(electric flux) 기호와 식 :
전기장,electric_field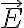 가 곡면,surface??
가 곡면,surface??  를 지난다면(통과한다면)
를 지난다면(통과한다면)
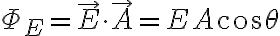
곡면  를 수많은 작은 면적(면적소)
를 수많은 작은 면적(면적소) 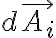 로 나누었다면
로 나누었다면
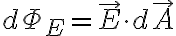
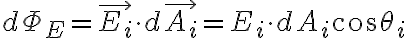
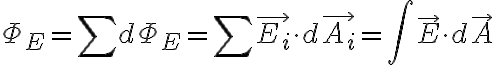
![[http]](/123/imgs/http.png) src가우스법칙(1)-앞부분 유실 10m
src가우스법칙(1)-앞부분 유실 10m
ΦE=EA
ΦE=E·A=EAcosθ
dΦE=E·dA
Φ=∫표면E·dA
...ΦE=E·A=EAcosθ
dΦE=E·dA
Φ=∫표면E·dA
작은 면 = dA
ΦE = ∫E cosθ dA
........typesetted:ΦE = ∫E cosθ dA
전기장,electric_field
![[http]](/123/imgs/http.png) src가우스법칙(1)-앞부분 유실 10m
src가우스법칙(1)-앞부분 유실 10m예전에적었던것

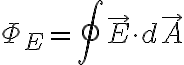
CLEANUP
4. 관련: 가우스 법칙 ¶
가우스_법칙,Gauss_s_law은
전하(q)를 둘러싸고 있는 폐곡면(S)과
폐곡면을 지나가는 전기장(E)의 관계식.
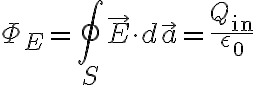
전하 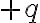 주변에 반지름
주변에 반지름  인 구가 있다. (구 표면 = 가우스 면)
인 구가 있다. (구 표면 = 가우스 면)
표면을 통과하는 전기선속은
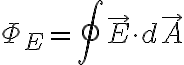
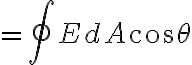 여기서
여기서 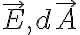 가 동일방향이므로
가 동일방향이므로
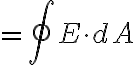 나오는 전기장
나오는 전기장 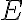 는 구 표면을 따라 일정하므로
는 구 표면을 따라 일정하므로
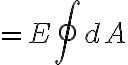
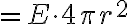
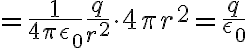
∴
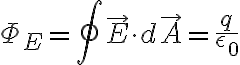
전하(q)를 둘러싸고 있는 폐곡면(S)과
폐곡면을 지나가는 전기장(E)의 관계식.
ΦE = q / ε0
가우스 폐곡면을 통과하는 전기장선속은 내부 전하 q와 비례.표면을 통과하는 전기선속은


![[https]](/123/imgs/https.png)