표기
1×1 행렬에서는 ![$A=[a]$ $A=[a]$](/123/cgi-bin/mimetex.cgi?\Large A=[a]) 일 때
일 때 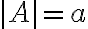
2×2 행렬에서
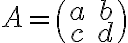 이면 그 행렬식은
이면 그 행렬식은 =\begin{vmatrix} a&b\\c&d \end{vmatrix}=ad-bc)
3×3 행렬에서
......TBW 여러 방법이 있는데,
사루스_규칙? Sarrus_rule (writing) { Rule_of_Sarrus ...
Rule_of_Sarrus ...  sarrus rule } <- 3x3에서만.
sarrus rule } <- 3x3에서만.
cofactor_expansion = Laplace_expansion (curr goto 여인수,cofactor) (is an 전개,expansion)
and?
(TODO '행렬식 구하는 법'을 별도의 문단으로 mk)
......TBW 여러 방법이 있는데,
사루스_규칙? Sarrus_rule (writing) {
cofactor_expansion = Laplace_expansion (curr goto 여인수,cofactor) (is an 전개,expansion)
and?
(TODO '행렬식 구하는 법'을 별도의 문단으로 mk)
0×0 행렬에서는 det[] = 0
1×1 행렬의 행렬식은 det[a]=a
2×2 행렬의 행렬식은

3×3 행렬의 행렬식은


4×4 행렬의 행렬식은

MKL
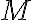 은 소행렬,minor or 소행렬,minor_matrix 보다는 minor_of_matrix 인 듯?
은 소행렬,minor or 소행렬,minor_matrix 보다는 minor_of_matrix 인 듯?  minor matrix
minor matrix  소행렬
소행렬  소행렬
소행렬
cofactor_expansion - 여인자,cofactor 전개,expansion i.e. 여인자전개,cofactor_expansion
1×1 행렬의 행렬식은 det[a]=a
2×2 행렬의 행렬식은
cofactor_expansion - 여인자,cofactor 전개,expansion i.e. 여인자전개,cofactor_expansion
Sub:
특성행렬식(characteristic determinant) characteristic_determinant - 별거 아니고 det(A-λI). 특성다항식,characteristic_polynomial과 마찬가지? 이걸 0으로 놓으면 특성방정식,characteristic_equation. (via: 고유값,eigenvalue의 앞부분 Kreyszig 인용)
resultant
헤세_행렬식,Hessian_determinant of 헤세_행렬,Hessian_matrix
resultant
헤세_행렬식,Hessian_determinant of 헤세_행렬,Hessian_matrix
1. 나눌 것 ¶
어떤 행렬 A의 행렬식 값
가역행렬,invertible_matrix은 행렬식이 0이 아니다.
det(A)=0 : ∄A−1 : A는 역행렬을 갖지 않는다.
det(A)≠0 : ∃A−1 : A의 역행렬이 존재한다.
i.e.det(A)≠0 : ∃A−1 : A의 역행렬이 존재한다.
가역행렬,invertible_matrix은 행렬식이 0이 아니다.
기하적으로는,
(대충) ~가(벡터,vectors들?) (서로 종속이 아니고 독립이어서) 넓이,area 부피,volume (.... 일반적으로 hypervolume?) 을 만들 수 있는지 '결정하는가'(hence the name)를 알려주는?
2차정사각행렬의 행렬식의 절대값은 두 벡터로 이루어진 평행사변형의 넓이,area, // 참고: (proof without words) determinant = area? https://lazymatlab.tistory.com/173
3차정사각행렬의 행렬식의 절대값은 세 벡터로 이루어진 평행육면체의 부피,volume CHK
3차정사각행렬의 행렬식의 절대값은 세 벡터로 이루어진 평행육면체의 부피,volume CHK
선형변환,linear_transformation의 스케일(scale) 성분을 나타낸다.
det의 부호에 따라
det의 부호에 따라
양이면 도형의 방향(orientation)이 보존되고,
음이면 도형의 방향이 보존되지 않는다.
[1]음이면 도형의 방향이 보존되지 않는다.
행렬에 의한 선형변환에 따른 면적 혹은 체적 변화율을 알아내고자 행렬식을 쓸 수 있다.
판별식,discriminant과 관계는?
(행렬식을 구하는 방법 중 하나)
어떤 구조에서 특징을 나타내는 실수 하나를 이끌어내본다 뭐 그런 아이디어는 비슷한 듯 한데
라플라스_전개,Laplace_expansion = 여인수 전개로 구할 수 있음. see 여인수,cofactor#s-2(행렬식을 구하는 방법 중 하나)
2. 성질 // from KUIAI, CHK ¶
기본연산과 행렬식
- A의 두 행(열)을 교환한 행렬이 B:
- A의 한 행(열)에 스칼라 c를 곱한 행렬이 B:
- 행렬의 스칼라 곱:
- A의 k번째 행(열)의 상수배를 j번째 행(열)에 더한 행렬이 B:
- A의 두 행(열)이 비례할 경우:
- 삼각행렬,triangular_matrix 및 대각행렬,diagonal_matrix의 행렬식:
주대각선 성분의 곱
- 항등행렬,identity_matrix의 행렬식:
 determinant of identity matrix
determinant of identity matrix
- 전치,transpose 연산:
- det(AB)=det(A)det(B)
- A가 가역행렬,invertible_matrix이면
이고,
이유는 간단.이므로
- A가 비가역행렬이면
3. tmp links ko ¶
행렬식의 성질 및 행렬의 동등정리(equivalent theorem): equivalence thm 아닌가?
http://blog.naver.com/mykepzzang/221121796109
(가역성(related: 가역행렬,invertible_matrix)은 매우 다양한 형태로 나타난다는 것을 알 수 있음.)
http://blog.naver.com/mykepzzang/221121796109
(가역성(related: 가역행렬,invertible_matrix)은 매우 다양한 형태로 나타난다는 것을 알 수 있음.)
7. Moore determinant ¶
curr see  Moore_matrix
Moore_matrix
저것의 행렬식은 Moore_determinant_over_a_finite_field
Moore_determinant_over_a_finite_field
다만 Moore_determinant_of_a_Hermitian_matrix도 있음에 주의
Moore_determinant_of_a_Hermitian_matrix도 있음에 주의
저것의 행렬식은
다만
11. 삼중곱과의 관계 및 행렬식의 세 조건 ¶
삼중곱,triple_product과의 관계 (삼중곱은 바로 앞에서 설명함)
그리고 임의의 n차원에서 세 가지 조건을 만족하는 함수가 항상 있으며 그게 바로 determinant라는 ..? chk
그리고 임의의 n차원에서 세 가지 조건을 만족하는 함수가 항상 있으며 그게 바로 determinant라는 ..? chk
See 김도형 http://www.kocw.net/home/search/kemView.do?kemId=1141060 5. (3차원 좌표체계, 내적과 외적) 1h:22m
대충 적으면,
2차원 평면과 그 위의 두 벡터 a1 a2 가 있을 때, 두 벡터로 결정되는 평행사변형의 넓이,area함수 A(a1, a2)가 있으면 A는 다음을 만족
① D(e1, e2)=1
② A(λa1, a2)=λA(a1, a2) 그리고 A(a1, λa2)=λA(a1, a2)
③ A(a1+a2, a2) = A(a1, a1+a2) = A(a1, a2)
이상 2차원 얘기였고
2차원에선 이게 ad−bc 바로 그거이고
3차원에선 벡터가 세개이며 부피,volume
n차원에서도 성립
2차원 평면과 그 위의 두 벡터 a1 a2 가 있을 때, 두 벡터로 결정되는 평행사변형의 넓이,area함수 A(a1, a2)가 있으면 A는 다음을 만족
① D(e1, e2)=1
② A(λa1, a2)=λA(a1, a2) 그리고 A(a1, λa2)=λA(a1, a2)
③ A(a1+a2, a2) = A(a1, a1+a2) = A(a1, a2)
이상 2차원 얘기였고
2차원에선 이게 ad−bc 바로 그거이고
3차원에선 벡터가 세개이며 부피,volume
n차원에서도 성립
12. 비교: 퍼머넌트 permanent ¶
ex. 2x2일 때
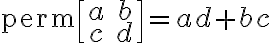
via https://brunch.co.kr/@sjoonkwon0531/21
{
det의 계산은 P class -) 이지만 perm의 계산은 그렇지 않다 - 훨씬 어렵다. 비교적 간단한 square mtx의 perm 계산도 NP-hard.
이지만 perm의 계산은 그렇지 않다 - 훨씬 어렵다. 비교적 간단한 square mtx의 perm 계산도 NP-hard.
}
{
det의 계산은 P class -
}
그리고 determinant와 permanent의 일반화는 이머넌트,immanant ?  Immanant라고 한다. https://mathworld.wolfram.com/Immanant.html
Immanant라고 한다. https://mathworld.wolfram.com/Immanant.html
https://mathworld.wolfram.com/Permanent.htmlhttps://planetmath.org/permanent
}
13. 표기법에 대해 (김홍종) ¶
정사각행렬 A의 행렬식을 기호 det A로 나타내는 대신에 |A|로 쓰는 저자도 있다. 이 편리한(?) 기호는, A의 절댓값을 나타내는 기호와 약간 혼동을 주고, 더 나아가서 치환적분법에서 중요하게 나타나는 행렬식의 절댓값을 ‖A‖로 나타내야 하는 부담을 준다. 우리는 기호 "det A"를 쓰기로 한다. 행렬식을 결정식이라고 부르는 이도 있다.
(김홍종 미적1+ p260 행렬식 각주)
14. 관련 개념: unimodularity and nonunimodularity ¶
unimodular adj. (격자,lattice나 행렬,matrix에 대해) 행렬식,determinant이 1 또는 −1인 성질. via  unimodular
unimodular
unimodularity n.
nonunimodular adj. Not unimodular. via nonunimodular
nonunimodular
nonunimodularity n.
대칭군
unimodularity n.
nonunimodular adj. Not unimodular. via
nonunimodularity n.
대칭군
이름은 '결정,determination'에서.
(아래의 경우 각각 2x2 행렬의 두 벡터, 3x3 행렬의 세 벡터 얘기)
2D 평면에서 두 벡터를 같은 시점으로 놓아 평행사변형,parallelogram을 만들어 0이 아닌 넓이,area를 가지는가 여부를 결정함.
3D 공간에서 세 벡터를 같은 시점으로 놓아 평행육면체,parallelepiped를 만들어 0이 아닌 부피,volume를 가지는가 여부를 결정함.
(종속(종속성,dependence)이 아닌 독립(독립성,independence)이어야 0이 아닌 저것을 만들 수 있음을 상기)
(이정일 https://youtu.be/hIRveiSlLnY?t=2056)
src? 뭐였더라
MKL 벡터,vector(아래의 경우 각각 2x2 행렬의 두 벡터, 3x3 행렬의 세 벡터 얘기)
2D 평면에서 두 벡터를 같은 시점으로 놓아 평행사변형,parallelogram을 만들어 0이 아닌 넓이,area를 가지는가 여부를 결정함.
3D 공간에서 세 벡터를 같은 시점으로 놓아 평행육면체,parallelepiped를 만들어 0이 아닌 부피,volume를 가지는가 여부를 결정함.
(종속(종속성,dependence)이 아닌 독립(독립성,independence)이어야 0이 아닌 저것을 만들 수 있음을 상기)
(이정일 https://youtu.be/hIRveiSlLnY?t=2056)
Twins:
행렬식 https://ghebook.blogspot.com/2011/06/determinant.html (어려움)
행렬식의 기하학적 의미 https://ghebook.blogspot.com/2011/06/geometric-meaning-of-determinant.html
https://ratsgo.github.io/linear algebra/2017/05/21/determinants/
3Blue1Brown: The determinant https://www.youtube.com/watch?v=Ip3X9LOh2dk
https://everything2.com/title/Determinant
https://mathworld.wolfram.com/Determinant.html (긺)
![[https]](/123/imgs/https.png) 수학백과: 행렬식
수학백과: 행렬식
 Determinant
Determinant
 행렬식
행렬식
https://planetmath.org/determinant
https://encyclopediaofmath.org/wiki/Determinant
행렬식 https://ghebook.blogspot.com/2011/06/determinant.html (어려움)
행렬식의 기하학적 의미 https://ghebook.blogspot.com/2011/06/geometric-meaning-of-determinant.html
https://ratsgo.github.io/linear algebra/2017/05/21/determinants/
3Blue1Brown: The determinant https://www.youtube.com/watch?v=Ip3X9LOh2dk
https://everything2.com/title/Determinant
https://mathworld.wolfram.com/Determinant.html (긺)
![[https]](/123/imgs/https.png) 수학백과: 행렬식
수학백과: 행렬식https://planetmath.org/determinant
https://encyclopediaofmath.org/wiki/Determinant
Up: 행렬,matrix

