표기와 용어
dx)
에서,
입체의 부피,volume 등을 구할 때 자주 쓰임
∫ : integral sign (적분기호)
f(x) : integrand (피적분함수)
x : variable of integration
a, b : limits of integration (적분한계)
곡선,curve 밑의 넓이,area(다만 그냥 넓이가 아닌 부호,sign가 있는 넓이)나f(x) : integrand (피적분함수)
x : variable of integration
a, b : limits of integration (적분한계)
a : lower limit (하한)
b : upper limit (상한)
b : upper limit (상한)
입체의 부피,volume 등을 구할 때 자주 쓰임
1. 정적분의 정의 ¶
함수 ) 가 구간
가 구간 ![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) 에서 연속일 때,
에서 연속일 때,
구간을 등분 하여 양 끝점과 각 분점의
등분 하여 양 끝점과 각 분점의  좌표를 차례로
좌표를 차례로
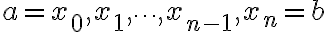
각 소구간의 길이는
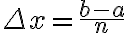
)
이 때
\Delta x+f(x_2)\Delta x+\cdots+f(x_k)\Delta x+\cdots+f(x_n)\Delta x)
\Delta x)
이면 극한값 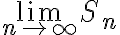 은 항상 존재하며, 이 극한값을
은 항상 존재하며, 이 극한값을
dx)
로 나타냄
구간을
함수 ) 의
의  에서
에서 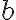 까지의 정적분
까지의 정적분
이라 하고여기서
dx=\lim_{n\to\infty}\sum_{k=1}^nf(x_k)\Delta x)
)
dx=\lim_{n\to\infty}\sum_{k=1}^{n}f(a+\frac{b-a}{n}\cdot k)\cdot\frac{b-a}{n})
a, b는 각각 아래끝, 위끝,
구간![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) : 적분 구간,
: 적분 구간,
) : 피적분함수,
: 피적분함수,
 : 적분변수
: 적분변수
구간
2. 미적분학의 기본정리에서 정적분 값 구하는 공식 이끌어내기 ¶
함수 ,f(x)) 가
가
=f(x))
를 만족하면, 미적분학의기본정리,FTC에서
dt=f(x)) 즉
즉
dt-\frac{d}{dx}F(x)=0)
이므로 모든  에 대해
에 대해
![$\frac{d}{dx}\left[\int_a^xf(t)dt-F(x)\right]=f(x)-f(x)=0$ $\frac{d}{dx}\left[\int_a^xf(t)dt-F(x)\right]=f(x)-f(x)=0$](/123/cgi-bin/mimetex.cgi?\Large \frac{d}{dx}\left[\int_a^xf(t)dt-F(x)\right]=f(x)-f(x)=0)
이다. 도함수가 0인 함수는 상수함수이므로
dt-F(x)=C)
이다. 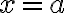 를 대입하면
를 대입하면 =C) 임을 알 수 있으므로
임을 알 수 있으므로
dt=F(x)-F(a))
정리: 함수 ) 가 구간
가 구간 ![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) 에서 연속이고
에서 연속이고 ) 가
가 ) 의 역도함수이면 다음이 성립.
의 역도함수이면 다음이 성립.
5. 회전체의 겉넓이 ¶
미분가능한 함수 ,\;a\le x\le b) 을
을  축 주위로 회전하여 생긴 회전체의 겉넓이:
축 주위로 회전하여 생긴 회전체의 겉넓이:
![$\int_a^b2\pi f(x)\sqrt{1+[f'(x)]^2}dx=\int_a^b2\pi yds$ $\int_a^b2\pi f(x)\sqrt{1+[f'(x)]^2}dx=\int_a^b2\pi yds$](/123/cgi-bin/mimetex.cgi?\Large \int_a^b2\pi f(x)\sqrt{1+[f%27(x)]^2}dx=\int_a^b2\pi yds)
TODO s등에 대한 설명이 부족함.. 길이함수
![$s(t)=\int_a^t\sqrt{1+[f'(x)]^2}dx$ $s(t)=\int_a^t\sqrt{1+[f'(x)]^2}dx$](/123/cgi-bin/mimetex.cgi?\Large s(t)=\int_a^t\sqrt{1+[f%27(x)]^2}dx) 를 이용하면, 즉
를 이용하면, 즉
![$ds=\sqrt{1+[f'(x)]^2}dx$ $ds=\sqrt{1+[f'(x)]^2}dx$](/123/cgi-bin/mimetex.cgi?\Large ds=\sqrt{1+[f%27(x)]^2}dx) 를 이용하면 다음과 같이 나타낼 수 있다는데.
를 이용하면 다음과 같이 나타낼 수 있다는데.
ds)
CLEANUP
6. Numerical methods for definite integrals ¶
left rule
right rule
midpoint rule
trapezoid rule
right rule
midpoint rule
trapezoid rule
Approximate Integration 정적분의 근사값 계산 later related to 근사,approximation
subinterval
하합 lower sum/상합 upper sum/midpoint rule 중점법
Simpson's rule 이차다항식,polynomial을 만들어 근사
Hermite's rule
subinterval
하합 lower sum/상합 upper sum/midpoint rule 중점법
QQQ lower/upper sum은 함수가 그 구간의 최소/최대일 때를 취한?
trapezoidal rule (사다리꼴) 을 만들어 근사, 즉 직선을 만들어 근사Simpson's rule 이차다항식,polynomial을 만들어 근사
Hermite's rule
사다리꼴 공식 or 사다리꼴 규칙(trapezoidal rule), 포물선 공식, Simpson's rule ..
ALSOIN 리만_합,Riemann_sum
8. 정적분의 성질 ¶
적분 순서 (리만_합,Riemann_sum에서 각 Δx의 부호가 변하므로, 극한값의 부호도 변한다.)
dx=-\int_b^a f(x)dx)
폭이 0인 구간
dx=0)
상수배
dx=k\int_a^b f(x)dx)
합과 차
\pm g(x))dx=\int_a^b f(x)dx\pm\int_a^b g(x)dx)
정적분의 가법성
dx+\int_b^c f(x)dx=\int_a^c f(x)dx)
최대-최소 부등식,inequality : 함수  가
가 ![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) 에서 최대값
에서 최대값 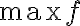 와 최소값
와 최소값 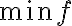 를 갖는다면
를 갖는다면
\le \int_a^b f(x)dx \le \max f \cdot (b-a))
지배성
![$f(x)\ge g(x)\text{ on }[a,b] \;\Rightarrow\; \int_a^b f(x)dx\ge \int_a^b g(x)dx$ $f(x)\ge g(x)\text{ on }[a,b] \;\Rightarrow\; \int_a^b f(x)dx\ge \int_a^b g(x)dx$](/123/cgi-bin/mimetex.cgi?\Large f(x)\ge g(x)\text{ on }[a,b] \;\Rightarrow\; \int_a^b f(x)dx\ge \int_a^b g(x)dx)
특별한 경우
![$f(x)\ge 0\text{ on }[a,b] \;\Rightarrow\; \int_a^b f(x)dx\ge 0$ $f(x)\ge 0\text{ on }[a,b] \;\Rightarrow\; \int_a^b f(x)dx\ge 0$](/123/cgi-bin/mimetex.cgi?\Large f(x)\ge 0\text{ on }[a,b] \;\Rightarrow\; \int_a^b f(x)dx\ge 0)
(Thomas 13e ko p255밑-257)
특별한 경우
9. 짝함수(우함수)의 정적분 / 홀함수(기함수)의 정적분 ¶
의 계산을 간단하게 할 수 있는 방법
짝함수(우함수)인  의 정적분 :
의 정적분 :
dx=2\int_0^a f(x)dx)
홀함수(기함수)인  의 정적분 :
의 정적분 :
dx=0)
10. 기타 ¶
이것은 정적분의 평균값정리,mean_value_theorem,MVT와도 밀접. 여기서도 또 서술하자면,
 가
가 ![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) 위에서 연속이면,
위에서 연속이면, ![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) 내의 한 점
내의 한 점 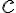 가 존재하여 다음 식이 성립한다.
가 존재하여 다음 식이 성립한다.
=\frac1{b-a}\int_a^b f(x)dx)
// tmp from https://m.blog.naver.com/cindyvelyn/222147098255 {
정적분의 일반화는 두 가지
정적분의 일반화는 두 가지
- 적분 구간이 x축이 아니라 곡선인 선적분,line_integral
- 적분을 여러 번 하는 (...차원을 높인?) 중적분,multiple_integral
Compare: 부정적분,indefinite_integral
Up: 적분,integration


![[https]](/123/imgs/https.png)