Up: Class_2021_1
Related:
교재:
Related:
교재:
Reading material:
Information Theory: A Tutorial Introduction - James V. Stone
Textbook:Contents
- 1. Resources
- 2. 03-02
- 3. 03-04 수업은 없음
- 4. 03-09 2주 1강
- 5. 03-11 2주 2
- 6. HW #1: Reading assignment: Chapter 1: What Is Information? 요약
- 7. HW #2: Reading assignment: Chapter 2: Entropy of Discrete Variables 요약
- 8. HW #3 (Homework Set 1) Notes
- 9. HW #4 : Problems
- 10. HW #4 : Chapter 4.1-4.6 요약
- 11. HW #6: Chapter 7(Channel Capacity: Continuous) 요약
2. 03-02 ¶
중간, 기말, 퀴즈하나, 간단한 프로그램 프로젝트 하나 생각 중. (잠정)
시험은 오픈북, 오프라인. 교재만 허용, 슬라이드 비허용, sticky notes 불가, 책에 적는 것은 ok.
coding theory보다는 information theory 다룸.
시험은 오픈북, 오프라인. 교재만 허용, 슬라이드 비허용, sticky notes 불가, 책에 적는 것은 ok.
coding theory보다는 information theory 다룸.
coin flipping얘기.
outcome(결과,outcome)이 백프로 확실한 것은 정보가 없음. no information.
next state가 확실한 system도 마찬가지.
large probability를 가진 것은 little information.
반면
rare outcome, small probability - large information.
outcome(결과,outcome)이 백프로 확실한 것은 정보가 없음. no information.
next state가 확실한 system도 마찬가지.
large probability를 가진 것은 little information.
반면
rare outcome, small probability - large information.
53m
2.1. information content ¶
확률,probability이 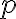 인 random event(사건,event)가 있을 때,
인 random event(사건,event)가 있을 때,
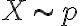
 의 information content는 이렇게 정의된다.
의 information content는 이렇게 정의된다.
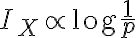
그러니까 inverse proportional의 log에 비례. 다시 쓰면
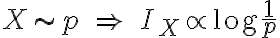
그냥 inverse proportional인 것도 언급. (TO REVIEW)
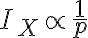
그런데 log가 들어간 이유는, negative information(?)을 다루기 위해서?
| large probability | small information |
| small probability | large information |
4. 03-09 2주 1강 ¶
First definition for measure of information
정보량 측정을 위해 Hartley(1928)가 로그,log를 도입.
:=\log_b r)
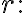 number of all possible outcomes of random variable
number of all possible outcomes of random variable 
Coin toss:
=\log_2 2\textrm{(1 bit)}=\log_e 2\textrm{(0.69 nats)})
(Hartley 정의의 문제?)
Hat 안에 black and white balls
A : BBWW ●●○○
B : BBBW ●●●○
Hartley 방법으로는, 모든 ball의 정보가 같다 (1 bit).
B 안의 black ball의 정보가 분명 더 적음에도 불구하고.
정보량 측정을 위해 Hartley(1928)가 로그,log를 도입.
| 밑 | 정보량의 단위 |
| 2 | bit |
| e | nat |
| 10 | Hartley |
Coin toss:
Hat 안에 black and white balls
A : BBWW ●●○○
B : BBBW ●●●○
Hartley 방법으로는, 모든 ball의 정보가 같다 (1 bit).
B 안의 black ball의 정보가 분명 더 적음에도 불구하고.
(그리하여 Shannon 정의가 등장?)
가능한 경우의_수,number_of_cases만 생각하지 않고, 확률까지 고려함.
경우의_수,number_of_cases만 생각하지 않고, 확률까지 고려함.
B에서
White balls: 확률 1/4, log24 = 2 bits
Black balls: 확률 3/4, log2(4/3) = 0.415 bits
가능한
B에서
White balls: 확률 1/4, log24 = 2 bits
Black balls: 확률 3/4, log2(4/3) = 0.415 bits
하얀 공: 1 out of 4 outcomes: =2) bits
bits
검은 공: 3 out of 4 outcomes: 1 out of 4/3 outcomes:=0.415) bits
bits
즉 로그 안에 확률의 역수를 넣음
검은 공: 3 out of 4 outcomes: 1 out of 4/3 outcomes:
즉 로그 안에 확률의 역수를 넣음
Combine: 평균
 bits
bits
Shannon's measure of information:
Average Hartley information with probability distribution of r outcomes:
=\sum_{i=1}^{r}p_i\log_2\frac{1}{p_i}=-\sum_{i=1}^{r}p_i\log_2 p_i)
(결과,outcome의 확률분포,probability_distribution 및 평균,mean,average을 활용)
Average Hartley information with probability distribution of r outcomes:
Probability가 uniform하다면 Hartley 정의도 좋지만 현실이 그렇지 않다.
5. 03-11 2주 2 ¶
binary entropy function
Definition
For binary random variable with two probability
with two probability =p) and
and =1-p)
![$H(X)=H_b(p):=-p\log_2 p-(1-p)\log_2(1-p),\;\;p\in[0,1]$ $H(X)=H_b(p):=-p\log_2 p-(1-p)\log_2(1-p),\;\;p\in[0,1]$](/123/cgi-bin/mimetex.cgi?\Large H(X)=H_b(p):=-p\log_2 p-(1-p)\log_2(1-p),\;\;p\in[0,1])
) is called binary entropy function
is called binary entropy function
For binary random variable
Information theory inequality
IT inequality
Useful inequality for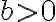 and
and 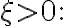
 \log_b e \le \log_b\xi \le (\xi-1)\log_b e)
with equalities on both sides iff 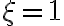
Useful inequality for
Proof by comparison of changes with derivatives evaluated at 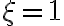
6. HW #1: Reading assignment: Chapter 1: What Is Information? 요약 ¶
표지 인물은 Claude Shannon (1916-2001)이다.
책 시작 부분은 다음 개념들
distance, mass, electric force, entropy, beauty, melody을 두 가지로 나눌 수 있고, entropy가 beauty, melody와 나란히(alongside) 놓일 수 있는 강력한 이유(grounds)가 있다는 말로 시작한다.
서문(Preface)
수학에선 통찰이 엄격보다 먼저 일어난다. 유명 물리학자들(Kepler, Newton, Fourier, Einstein)은 (순수 수학과는 다른) 물리적 세계에서 얻은 통찰에서부터 이론을 이끌어냈다. 그래서 이 책도 '어떻게' 정보이론이 작동하는지를, 그리고 '왜' 그렇게 작동하는지를 이야기하고자 한다. 이것은 섀넌의 접근법과 마찬가지 방법이다.
이 책에선 엄밀한 수학적 접근을 회피한다. 섀넌은 순수수학의 지나친 엄격성이 분석의 주 끈을 희미하게 할 수 있다고 말한다. (obscure the main thread of the analysis) 비슷한 맥락으로, Jaynes는 집합이나 공간 X를 먼저 이야기하는 주문(incantation)을 걸지 않고 변수 x를 소개하면 비정의문제(undefined problem)를 다루는 일을 다룬다는 혐의를 받을(accused of) 수 있다고 말한다.
간단히 말해 엄밀함을 포기하고 쉽게 설명한다는 얘기.
수학에선 통찰이 엄격보다 먼저 일어난다. 유명 물리학자들(Kepler, Newton, Fourier, Einstein)은 (순수 수학과는 다른) 물리적 세계에서 얻은 통찰에서부터 이론을 이끌어냈다. 그래서 이 책도 '어떻게' 정보이론이 작동하는지를, 그리고 '왜' 그렇게 작동하는지를 이야기하고자 한다. 이것은 섀넌의 접근법과 마찬가지 방법이다.
이 책에선 엄밀한 수학적 접근을 회피한다. 섀넌은 순수수학의 지나친 엄격성이 분석의 주 끈을 희미하게 할 수 있다고 말한다. (obscure the main thread of the analysis) 비슷한 맥락으로, Jaynes는 집합이나 공간 X를 먼저 이야기하는 주문(incantation)을 걸지 않고 변수 x를 소개하면 비정의문제(undefined problem)를 다루는 일을 다룬다는 혐의를 받을(accused of) 수 있다고 말한다.
간단히 말해 엄밀함을 포기하고 쉽게 설명한다는 얘기.
언급된 자료/링크
매트랩 코드 http://jim-stone.staff.shef.ac.uk/BookInfoTheory/InfoTheoryMatlab.html
파이썬 코드(2.7) http://jim-stone.staff.shef.ac.uk/BookInfoTheory/InfoTheoryPython.html
오류수정 http://jim-stone.staff.shef.ac.uk/BookInfoTheory/Corrections.html
매트랩 코드 http://jim-stone.staff.shef.ac.uk/BookInfoTheory/InfoTheoryMatlab.html
파이썬 코드(2.7) http://jim-stone.staff.shef.ac.uk/BookInfoTheory/InfoTheoryPython.html
오류수정 http://jim-stone.staff.shef.ac.uk/BookInfoTheory/Corrections.html
1장: 정보란 무엇인가?
1.1. 소개
정보는 우주를 구성하는 기본적 양(quantity)이며 질량/속도 같은 것 이상으로 중요하다.
1948년 섀넌 논문 발표 : A Mathematical Theory of Communication
섀넌 전에는 정보는 형편없이 정의된 유독한 액체(poorly defined miasmic fluid)처럼 보였다. 하지만 논문 이후로 잘 정의되고 측정가능한 양임이 명백해졌다.
1.1. 소개
정보는 우주를 구성하는 기본적 양(quantity)이며 질량/속도 같은 것 이상으로 중요하다.
1948년 섀넌 논문 발표 : A Mathematical Theory of Communication
섀넌 전에는 정보는 형편없이 정의된 유독한 액체(poorly defined miasmic fluid)처럼 보였다. 하지만 논문 이후로 잘 정의되고 측정가능한 양임이 명백해졌다.
1.2. 정보, 눈 그리고 진화
섀넌 이론은,
섀넌 이론은,
- 정보의 수학적 정의를 줌.
- 서로 다른 system의 element간에 얼마나 많이 통신될(communicated) 수 있는지 정확히 설명함.
1.3.
일반적인 정보 단위: 비트(bit). 어원은 binary digit. 그러나 앞으로 보겠지만 bit와 binary digit는 근본적으로 다른 (개체/실체/독립체)이다. (fundamentally different types of entities)
수형도 나옴. (이진 트리)
정보 1비트로는 2개의 대안(alternatives, 선택 가능한 것).
정보 2비트로는 4개의 대안.
정보 n비트로는 2n개의 대안.
2의 n제곱과, binary log 스무고개 언급.
일반적인 정보 단위: 비트(bit). 어원은 binary digit. 그러나 앞으로 보겠지만 bit와 binary digit는 근본적으로 다른 (개체/실체/독립체)이다. (fundamentally different types of entities)
수형도 나옴. (이진 트리)
정보 1비트로는 2개의 대안(alternatives, 선택 가능한 것).
정보 2비트로는 4개의 대안.
정보 n비트로는 2n개의 대안.
2의 n제곱과, binary log 스무고개 언급.
1.4. 20개 물음에 대한 백만 개의 답
스무고개 이야기. 1,048,576=220, 그래서 20개의 Yes/No 질문으로 백만 개의 개념을 가려낼 수 있음.
스무고개 이야기. 1,048,576=220, 그래서 20개의 Yes/No 질문으로 백만 개의 개념을 가려낼 수 있음.
1.5. 정보, 비트, binary digits
비트의 어원은 바이너리 디지트이지만, 다른 점이 있다. 사소하지만 중요한(subtle but vital).
MacKay(2003)는 정보의 단위를 Shannon으로 제안함.
(반복) Key Point:
1845년 전신으로 속보를 보내 살인자를 체포한 이야기 언급.
1830년 Morse와 Vail은 Morse code를 만듦. 자주 쓰이는 e, t에 짧은 코드가, 덜 쓰이는 j, z등에 긴 코드가 배정되어 있다.
비트의 어원은 바이너리 디지트이지만, 다른 점이 있다. 사소하지만 중요한(subtle but vital).
- binary digit: 이진 변수 값(value of a binary variable), 값은 0 또는 1. 하지만 정보 그 자체는 아니다(not information per se).
- bit: 정보이다.
MacKay(2003)는 정보의 단위를 Shannon으로 제안함.
(반복) Key Point:
- bit: 정보의 양(amount of information). 확률이 같은 두 것들 중 고르는 것 같은. (e.g. left/right)
- binary digit: 이진 변수의 값. 두 가능한 값 중 하나를 채택(adopt)하는. (i.e. 0/1)
1845년 전신으로 속보를 보내 살인자를 체포한 이야기 언급.
1830년 Morse와 Vail은 Morse code를 만듦. 자주 쓰이는 e, t에 짧은 코드가, 덜 쓰이는 j, z등에 긴 코드가 배정되어 있다.
1.7. Example 2: Binary Images
pixel의 어원(picture element) 언급. 흑백 이미지 및 RLE언급.
pixel의 어원(picture element) 언급. 흑백 이미지 및 RLE언급.
1.8. Example 3: Grey-Level Images
그레이스케일 이미지에서 인접한 픽셀은 완전히 독립적이지 않다. 즉 어느 정도의 중복(a degree of redundancy)이 있다.
(다시 말해, 대부분 이미지에선 그레이레벨이 완전히 확 바뀌는 경우가 적다.)
간단한 방법인 difference coding 언급. 소리 전송에서 이것 중 한 방법인 difference pulse code modulation이 쓰인다.
이미지의 히스토그램을 언급. 그레이레벨 차이 사진은 정보량(단위 bits/pixel)이 더 적다.
0.5비트 같은 소수 비트(fraction of a bit)는 처음엔 이상하게 보일 수 있겠지만, 8비트 그레이스케일 한 픽셀이 하드디스크에 4비트로 저장될 수 있다.
그레이스케일 이미지에서 인접한 픽셀은 완전히 독립적이지 않다. 즉 어느 정도의 중복(a degree of redundancy)이 있다.
(다시 말해, 대부분 이미지에선 그레이레벨이 완전히 확 바뀌는 경우가 적다.)
간단한 방법인 difference coding 언급. 소리 전송에서 이것 중 한 방법인 difference pulse code modulation이 쓰인다.
이미지의 히스토그램을 언급. 그레이레벨 차이 사진은 정보량(단위 bits/pixel)이 더 적다.
0.5비트 같은 소수 비트(fraction of a bit)는 처음엔 이상하게 보일 수 있겠지만, 8비트 그레이스케일 한 픽셀이 하드디스크에 4비트로 저장될 수 있다.
1.9 Summary
이상 2(갈랫길에서의 fork), 26(영문자), 256(픽셀 그레이레벨)을 봐 왔음. 데이터의 redundancy로 인해 압축이 될 수 있다. 이런 여유도,redundancy가 강조하는 키포인트: binary digit가 한 비트의 정보만 제공하는 게 아니라는 것.
이상 2(갈랫길에서의 fork), 26(영문자), 256(픽셀 그레이레벨)을 봐 왔음. 데이터의 redundancy로 인해 압축이 될 수 있다. 이런 여유도,redundancy가 강조하는 키포인트: binary digit가 한 비트의 정보만 제공하는 게 아니라는 것.
단어/표현 정리
(추천사) A crackingly clear tutorial for beginners.
cavalier adj. 무신경한
incantation n. (마술을 걸기 위한) 주문
inexorably adv. 냉혹하게, 가차없이
(1.1) The universe is conventionally described in terms of physical quantities such as mass and velocity, but a quantity at least as important as these is information.
(1.9) unfettered adj. 제한받지 않는, 규제가 없는
(추천사) A crackingly clear tutorial for beginners.
crackingly : cracking=very, extremely. https://www.merriam-webster.com/dictionary/cracking
(Preface) In math, rigour follows insight, and not vice versa.A follows B는, A가 B를 따른다, 즉 시간 순서에서 B가 먼저 온다는 말.
통찰(이해, 인사이트)이 철저(엄격)에 앞선다. 그 반대는 아니다.
in a similar vein : 비슷한 맥락에서통찰(이해, 인사이트)이 철저(엄격)에 앞선다. 그 반대는 아니다.
cavalier adj. 무신경한
incantation n. (마술을 걸기 위한) 주문
inexorably adv. 냉혹하게, 가차없이
(1.1) The universe is conventionally described in terms of physical quantities such as mass and velocity, but a quantity at least as important as these is information.
at least as important as these : 이것들 이상으로 중요하다. (즉 중요도가 같거나 더 중요하다. 하지만 덜 중요하지는 않다는 뜻.)
(1.3) entity n. 개체, 실체, 독립체(1.9) unfettered adj. 제한받지 않는, 규제가 없는
7. HW #2: Reading assignment: Chapter 2: Entropy of Discrete Variables 요약 ¶
2장: 이산변수의 엔트로피
2.1. 소개
먼저 확률(probability), 이산변수(discrete variables), 확률변수(random variables)로 기초를 깐다. 그 다음에 엔트로피를 논할 수 있다.
먼저 확률(probability), 이산변수(discrete variables), 확률변수(random variables)로 기초를 깐다. 그 다음에 엔트로피를 논할 수 있다.
2.2. 기본법칙과 용어
확률은 상대빈도(relative frequency) 관련.
확률은 상대빈도(relative frequency) 관련.
변수 ↔ 분포(distribution)
이산변수(discrete variables) ↔ 확률함수(probability funciton)
연속변수(continuous variables) ↔ 확률밀도함수(PDF)
이산변수(discrete variables) ↔ 확률함수(probability funciton)
연속변수(continuous variables) ↔ 확률밀도함수(PDF)
확률변수(random variable), 표본공간(sample space), 결과(outcome), 메시지(message: symbol의 ordered sequence), 통신채널(communication channel)를 정의함.
메시지(message)
메시지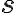 가 인코더(encoder, 채널입력을 하는 함수)를 통해
가 인코더(encoder, 채널입력을 하는 함수)를 통해 ) 로 변환.
로 변환.
채널입력(channel input)은 코드워드의 열(sequence of codewords)
,)
이고 각 코드워드(codeword)는 확률변수  의 값이며, 이것은 코드북의
의 값이며, 이것은 코드북의 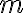 개의 다른 값 중 하나. 코드북(codebook)은
개의 다른 값 중 하나. 코드북(codebook)은
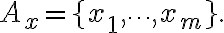
각 코드워드의 확률은
=\lbrace p(x_1),\cdots,p(x_m)\rbrace .)
코드(code) : 기호들과 그에 대응하는 코드워드의 목록. (a list of symbols and their corresponding codewords). 간단한 lookup table로 상상해 볼 수 있다.
메시지
채널입력(channel input)은 코드워드의 열(sequence of codewords)
채널용량(channel capacity). 노이즈에 의해 전송되는 비트 양이 감소하는 그림.
Key Point. (p. 30) A message comprising symbols
)
is encoded by a function
)
into a sequence of codewords
,)
where the number of symbols and codewords are not necessarily equal. These codewords are transmitted through a communication channel to produce outputs
)
which are decoded to recover the message 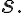
2.3. Shannon's Desiderata (섀넌이 필요로 했던 것)
정보의 수학적 정의가 유용하려면 몇가지 최소한의 성질이 있어야 한다고 생각했다.
1. 연속성(continuity) : 결과(outcome)에 대한 정보의 양은, 결과의 확률 변화에 따라 부드럽게(연속적으로) 증감한다.
2. 대칭성(symmetry) : 결과열(sequence of outcomes)에 대한 정보의 양은, 결과의 순서에 의존하지 않는다.
3. 극대값? 최대값? (maximal value) : 결과 집합(set of outcomes)에 대한 정보의 양은, 결과들이 이미 확률이 같다면 증가하지 않는다.
4. 가산적(additive) : 결과 집합에 대한 정보의 양은, 개별 결과의 정보의 합으로 얻을 수 있다.
정보의 수학적 정의가 유용하려면 몇가지 최소한의 성질이 있어야 한다고 생각했다.
1. 연속성(continuity) : 결과(outcome)에 대한 정보의 양은, 결과의 확률 변화에 따라 부드럽게(연속적으로) 증감한다.
2. 대칭성(symmetry) : 결과열(sequence of outcomes)에 대한 정보의 양은, 결과의 순서에 의존하지 않는다.
3. 극대값? 최대값? (maximal value) : 결과 집합(set of outcomes)에 대한 정보의 양은, 결과들이 이미 확률이 같다면 증가하지 않는다.
4. 가산적(additive) : 결과 집합에 대한 정보의 양은, 개별 결과의 정보의 합으로 얻을 수 있다.
2.4. 정보, 놀라움, 엔트로피(Information, Surprise and Entropy)
확률이 적을 때 더 놀랍다. 놀라움의 정도는 확률에 반비례. 즉.) 위의 additive 조건을 만족시키려면 놀라움을 그것의 로그로 정의하는 것이 좋다고 함. 이것을 Shannon information of
위의 additive 조건을 만족시키려면 놀라움을 그것의 로그로 정의하는 것이 좋다고 함. 이것을 Shannon information of  라고 한다.
라고 한다.
즉 surprise의 measure인 Shannon information은
=\log_2(1/p(x))=-\log_2 p(x)) (단위는 bits)
(단위는 bits)
엔트로피(entropy)는 평균 Shannon information. (확률까지 고려한)
\approx \frac1n \sum_{i=1}^n \log \frac1{p(x_i)})
확률이 같은 결과값 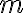 개가 있다면 확률변수의 엔트로피는
개가 있다면 확률변수의 엔트로피는
=\log m \textrm{ bits})
Key Point (p. 36) A variable with an entropy of ) bits provides enough Shannon information to choose between
bits provides enough Shannon information to choose between }) equally probable alternatives.
equally probable alternatives.
확률이 적을 때 더 놀랍다. 놀라움의 정도는 확률에 반비례. 즉
즉 surprise의 measure인 Shannon information은
Key Point (p. 42) The average uncertainty of a variable  is summarised by its entropy
is summarised by its entropy .) If we are told the value of
If we are told the value of  then the amount of information we have been given is, on average, exactly equal to its entropy.
then the amount of information we have been given is, on average, exactly equal to its entropy.
Key Point (p. 42) Doubling the number of possible values of a variable adds one bit to its entropy.
Key Point (p. 43) The entropy of a discrete variable depends only on the probability distribution of its values. Changing the values of a discrete variable does not change its entropy provided the number of values stays the same.
2.7.
iid = independent and identically distributed
iid = independent and identically distributed
2.8.
밑을 e로 한 단위는 nats. 밑을 10으로 한 단위는 bans. 밑을 2로 한 단위는 Shannon(Sh).
밑을 e로 한 단위는 nats. 밑을 10으로 한 단위는 bans. 밑을 2로 한 단위는 Shannon(Sh).
단어정리
envisage v. 예상하다, 상상하다
desideratum n. 필요물, 필요한 것 (pl. desiderata)
additive n. 첨가물, 첨가제; adj. 가산적
envisage v. 예상하다, 상상하다
desideratum n. 필요물, 필요한 것 (pl. desiderata)
additive n. 첨가물, 첨가제; adj. 가산적
8. HW #3 (Homework Set 1) Notes ¶
1. (Coin flips.)
see 1 3 of https://www.maths.tcd.ie/~houghton/MA3466/11-12/PS.php
see 1 of http://www.ee.imperial.ac.uk/hp/staff/dmb/courses/infotheory/probc1.pdf
2. (Entropy of functions.)
see 3 1 of https://www.maths.tcd.ie/~houghton/MA3466/11-12/PS.php
3. (Entropy of functions of a random variable.)
see 3 2 of https://stackoverflow.com/questions/57644910/shannon-entropy-one-variable-is-function-of-the-other-bijective-vs-injective-c
4. (Zero conditional entropy.)
https://math.stackexchange.com/questions/3383199/conditional-entropy-if-hyx-0-then-there-exists-a-function-g-such-that
see 6 of http://www.ee.imperial.ac.uk/hp/staff/dmb/courses/infotheory/probc1.pdf
5. (Coin weighing.)
see 2 2. (a)
see 1 3 of https://www.maths.tcd.ie/~houghton/MA3466/11-12/PS.php
see 1 of http://www.ee.imperial.ac.uk/hp/staff/dmb/courses/infotheory/probc1.pdf
2. (Entropy of functions.)
see 3 1 of https://www.maths.tcd.ie/~houghton/MA3466/11-12/PS.php
3. (Entropy of functions of a random variable.)
see 3 2 of https://stackoverflow.com/questions/57644910/shannon-entropy-one-variable-is-function-of-the-other-bijective-vs-injective-c
4. (Zero conditional entropy.)
https://math.stackexchange.com/questions/3383199/conditional-entropy-if-hyx-0-then-there-exists-a-function-g-such-that
see 6 of http://www.ee.imperial.ac.uk/hp/staff/dmb/courses/infotheory/probc1.pdf
5. (Coin weighing.)
see 2 2. (a)
9. HW #4 : Problems ¶
1. p3 of https://my.ece.utah.edu/~rchen/courses/homework1_sol_rr.pdf
2. exercise 3 of https://perso.telecom-paristech.fr/tchamker/SOCOM205/2017/hw3_sol.pdf
3. sheet 4 problem 4 of https://www.maths.tcd.ie/~houghton/MA3466/11-12/PS.php
4.
5. p6 of https://my.ece.utah.edu/~rchen/courses/homework1_sol_rr.pdf
2. exercise 3 of https://perso.telecom-paristech.fr/tchamker/SOCOM205/2017/hw3_sol.pdf
3. sheet 4 problem 4 of https://www.maths.tcd.ie/~houghton/MA3466/11-12/PS.php
4.
5. p6 of https://my.ece.utah.edu/~rchen/courses/homework1_sol_rr.pdf
10. HW #4 : Chapter 4.1-4.6 요약 ¶
Chapter 4: The Noisy Channel Coding Theorem
4.1. 소개
상호정보(mutual information) is general measure of association between two variables, like the input and output of a communication channel.
이산변수와 연속변수에 둘 다 해당되는 내용부터 먼저 알아본다.
상호정보(mutual information) is general measure of association between two variables, like the input and output of a communication channel.
이산변수와 연속변수에 둘 다 해당되는 내용부터 먼저 알아본다.
두 변수 X,Y가 있을 때, 둘 사이의 상호정보 I(X,Y)는, X의 한 값을 관측한 다음 얻는 Y에 대한 평균 정보이다.
다른 말로는, Y의 값을 알게 됨으로 인한 X에 대한 불확실성(uncertainty)의 평균 감소(reduction)이다.
그리고 X와 Y를 바꾸어도 마찬가지다(and vice versa).
다른 말로는, Y의 값을 알게 됨으로 인한 X에 대한 불확실성(uncertainty)의 평균 감소(reduction)이다.
그리고 X와 Y를 바꾸어도 마찬가지다(and vice versa).
좀 덜 간단한 정의를 하면, Y 값에 대한 불확실성은, 초기에 그것의 엔트로피 H(Y)로 요약될 수 있다. X와 Y가 관련되어 있다면, X의 값 하나를 관측하고 나면 Y의 정보를 더 알 수 있고, (이것이 반복되면) Y의 대한 불확실성은 H(Y)보다 작게 감소된다. X, Y의 가능한 모든 값 사이 평균을 내고, X를 관찰하면, Y에 대한 불확실성은 X와 Y사이의 상호정보 I(X,Y) 만큼 감소한다. X의 한 값을 관측했음에도 Y에 대해 남아 있는 불확실성은 조건부엔트로피(conditional entropy) H(Y|X)이다.
4.2. 결합분포 Joint Distributions (see 결합확률분포,joint_probability_distribution)
결합확률분포의 엔트로피(entropy of the joint probability distribution):
![$\begin{align}H(X,Y)&=&\sum_{i=1}^{m_x}\sum_{j=1}^{m_y}p(x_i,y_j)\log\frac{1}{p(x_i,y_j)}\\&=&E\left[\log\frac{1}{p(x,y)}\right]\textrm{ bits per pair}\end{align}$ $\begin{align}H(X,Y)&=&\sum_{i=1}^{m_x}\sum_{j=1}^{m_y}p(x_i,y_j)\log\frac{1}{p(x_i,y_j)}\\&=&E\left[\log\frac{1}{p(x,y)}\right]\textrm{ bits per pair}\end{align}$](/123/cgi-bin/mimetex.cgi?\Large \begin{align}H(X,Y)&=&\sum_{i=1}^{m_x}\sum_{j=1}^{m_y}p(x_i,y_j)\log\frac{1}{p(x_i,y_j)}\\&=&E\left[\log\frac{1}{p(x,y)}\right]\textrm{ bits per pair}\end{align})
where
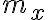 : the number of different values of
: the number of different values of 
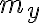 : the number of different values of
: the number of different values of 
(4.10)
결합확률분포의 엔트로피(entropy of the joint probability distribution):
X와 Y가 독립이면
=p(x_i)p(y_j))
=p(X)p(Y))
(4.18)
+H(Y)-H(X,Y)=0) bits per outcome pair
bits per outcome pair
(4.25)
4.3. Mutual Information
=\sum_{i=1}^{m_x}\sum_{j=1}^{m_y}p(x_i,y_j)\log\frac{p(x_i,y_j)}{p(x_i)p(y_j)})
![$I(X,Y)=E\left[\log\frac{p(x,y)}{p(x)p(y)}\right]$ $I(X,Y)=E\left[\log\frac{p(x,y)}{p(x)p(y)}\right]$](/123/cgi-bin/mimetex.cgi?\Large I(X,Y)=E\left[\log\frac{p(x,y)}{p(x)p(y)}\right]) bits
bits
(4.31)
By symmetry,
The entropy of the noise is the conditional entropy:
=H(\eta))
(4.60)
=H(Y)-I(X,Y))
(4.61)
4.5. Noise and Cross-Talk
H(X) : input entropy
H(Y) : output entropy
H(X, Y) : joint entropy
I(X, Y) : mutual information
H(X|Y) and H(Y|X) : conditional entropies
의 관계. (Figure 4.5 참조)
H(X) : input entropy
H(Y) : output entropy
H(X, Y) : joint entropy
I(X, Y) : mutual information
H(X|Y) and H(Y|X) : conditional entropies
의 관계. (Figure 4.5 참조)
4.6. Noisy Pictures and Coding Efficiency
여기서는 위에서 알아본 식들을 사용하여 noisy picture를 분석.
여기서는 위에서 알아본 식들을 사용하여 noisy picture를 분석.
11. HW #6: Chapter 7(Channel Capacity: Continuous) 요약 ¶
정보는 근본적 물리량이다. (fundamental physical quantity)
7.1 Introduction
연속확률변수,continuous_random_variable의 입력분포(input distribution)) 가 어떤 형태여야, noisy channel을 통한 통신의 비율,rate을 최대화하는지 알아본다. 채널용량을 정의한 뒤,
가 어떤 형태여야, noisy channel을 통한 통신의 비율,rate을 최대화하는지 알아본다. 채널용량을 정의한 뒤,
정의:
} I(X,Y) \;\textrm{ bits})
여기서 ) 는 상호정보,mutual_information
는 상호정보,mutual_information
=H(Y)-H(Y|X) \;\textrm{ bits})
다음 두 가지 제약,constraint 하에서, 정보전송(information transmission)을 최대화하는 입력분포(input distribution)를 알아볼 예정.
가우시안 채널이란, noise가 가우스_분포Gaussian_distribution(⇒ 정규분포,normal_distribution)를 갖는 채널,channel. 채널출력이 고정된 분산,variance을 가지면, 그것의 엔트로피,entropy는 가우스분포를 가질 때 최대화된다는 것을 안다.
연속확률변수,continuous_random_variable의 입력분포(input distribution)
● 최대 communication rate를 제공하는 input distribution이, 고려할 channel의 본성/성질(nature)에 의존함을 알아본다.
(원문: we find that the input distribution which provides the maximum communication rate depends on the nature of the channel under consideration.)
● 또한, 이산변수와 공동으로, 오류율(error rate)이 메시지 길이가 증가함에 따라 급격히 줄어듦을 알아본다.
(원문: In common with discrete variables, we also find that the error rate shrinks rapidly as the message length increases.)
7.2 채널용량,channel_capacity(원문: we find that the input distribution which provides the maximum communication rate depends on the nature of the channel under consideration.)
● 또한, 이산변수와 공동으로, 오류율(error rate)이 메시지 길이가 증가함에 따라 급격히 줄어듦을 알아본다.
(원문: In common with discrete variables, we also find that the error rate shrinks rapidly as the message length increases.)
정의:
- 출력은 고정된 분산,variance와 무한한 range를 가짐.
(물리적 비유: 고정된(specific) power(전력,power, 일률,power) 하에서 스피커로 전달되는 소리,sound 신호. 왜냐면 power equates to variance.)
- 출력은 유한한 range를 가짐.
(비유: 카메라 광수용기(photoreceiptor) - 0 V가 최소, 5 V가 최대인.)
가우시안 채널이란, noise가 가우스_분포Gaussian_distribution(⇒ 정규분포,normal_distribution)를 갖는 채널,channel. 채널출력이 고정된 분산,variance을 가지면, 그것의 엔트로피,entropy는 가우스분포를 가질 때 최대화된다는 것을 안다.
그럼 질문: channel의 입력-출력 사이 상호정보,mutual_information를 최대하하기 위해서, 입력분포 ) 는 어떤 형태(form)를 채택해야(adopt) 하는가? 지금까지 우리는 관련된 두 개의 사실을 알고 있다.
는 어떤 형태(form)를 채택해야(adopt) 하는가? 지금까지 우리는 관련된 두 개의 사실을 알고 있다.
1. 신호,signal  가 채널을 통과하면서 첨가되는 noise는
가 채널을 통과하면서 첨가되는 noise는
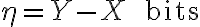
2. 입력 X와 출력 Y 사이의 상호정보는
=H(Y)-H(Y|X) \;\textrm{ bits})
그런데 식 4.60에 따르면 channel noise는 =H(\eta)) 이므로
이므로
=H(Y)-H(\eta) \;\textrm{ bits})
그래서 channel capacity를 다시 쓰면
} H(Y)-H(\eta) \;\textrm{ bits})
상호정보를 최대화하는 시도를 한다면, noise entropy를 감소시킬수는 없다. (channel의 fixed property이므로) 따라서 출력 Y의 엔트로피를 최대화하는 수 밖에 없다.
두 가우스변수Gaussian_variable의 합 또한 Gaussian이다.
(...)
입력, 출력, noise가 모두 Gaussian이면, ●출력값 당 통신된 정보의 평균량은, 채널용량(원문: the average amount of information communicated per output value is the channel capacity)
=H(Y)-H(\eta)=C \;\textrm{ bits})
이 결과는, 다음 정리의 비공식적 증명(informal proof)이다. ●"섀넌의 연속적 잡음있는 채널 코딩 정리 for 가우시안 채널"(원문: Shannon’s continuous noisy channel coding theorem for Gaussian channels)
(...)
입력, 출력, noise가 모두 Gaussian이면, ●출력값 당 통신된 정보의 평균량은, 채널용량(원문: the average amount of information communicated per output value is the channel capacity)
noise의 variance가 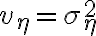 이면
이면
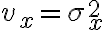 을 가지면
을 가지면
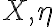 가 각각 variance
가 각각 variance 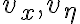 을 가지면, 제3의 변수
을 가지면, 제3의 변수 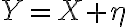 또한 Gaussian이며 variance는
또한 Gaussian이며 variance는 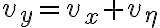 이다. 그래서
이다. 그래서  의 엔트로피는
의 엔트로피는 =\frac12\log 2\pi ev_y=\frac12\log 2\pi e(v_x+v_\eta) \;\textrm{ bits}) 가 된다. 종합하면
가 된다. 종합하면
-\frac12\log 2\pi ev_{\eta}\\&=\frac12\log\frac{v_x+v_{\eta}}{v_{\eta}}\\&=\frac12\log\left( 1+\frac{v_x}{v_{\eta}} \right ) \;\textrm{ bits}\end{align})
모든 signal의 variance는 그것의 power와 같으므로, input signal power 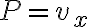 그리고 noise power
그리고 noise power 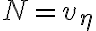 로 하면, Gaussian channel의 capacity 식은
로 하면, Gaussian channel의 capacity 식은
 \;\textrm{ bits})
여기서 variances의 ratio  : signal to noise ratio (SNR) - 신호대잡음비
: signal to noise ratio (SNR) - 신호대잡음비
(...)
엔트로피는 =\frac12\log 2\pi ev_{\eta}\;\textrm{ bits})
비슷하게, 입력이 variance 엔트로피는 =\frac12\log 2\pi ev_x \;\textrm{ bits})
두 독립적 가우스변수 (...)
긴 메시지들(Long Messages)
지금까지는 single input/output pairs of values만 고려했다. error rates(에러율, curr goto 오차,error)를 다루는 다음 섹션을 이해하기 위해, 둘 이상의 값으로 이루어진 codewords와 messages(메시지,message)를 고려할 필요가 있다.
각 encoded message x가 n-vector) 이라 하고, 각 값이 한 message symbol에 대응한다고, 그래서 message length와 codeword length가 같다고 가정한다.
이라 하고, 각 값이 한 message symbol에 대응한다고, 그래서 message length와 codeword length가 같다고 가정한다.
각 encoded message는 channel을 통과하는 도중 noise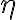 에 의해 훼손되므로(corrupted)
에 의해 훼손되므로(corrupted)  각 값은 대응하는 출력값
각 값은 대응하는 출력값 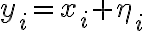 에 관련된다. 여기서 y는 n-vector 수신 출력(received output). noisy version of the encoded message는
에 관련된다. 여기서 y는 n-vector 수신 출력(received output). noisy version of the encoded message는
=(x_1+\eta_1,\cdots,x_n+\eta_n)=(x_1,\cdots,x_n)+(\eta_1,\cdots,\eta_n)=\vec{x}+\eta)
여기서 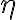 는 noise values의 벡터
는 noise values의 벡터 .)
(...) 7.3 이하, 7.4, 7.5 생략
지금까지는 single input/output pairs of values만 고려했다. error rates(에러율, curr goto 오차,error)를 다루는 다음 섹션을 이해하기 위해, 둘 이상의 값으로 이루어진 codewords와 messages(메시지,message)를 고려할 필요가 있다.
각 encoded message x가 n-vector
각 encoded message는 channel을 통과하는 도중 noise
(...) 7.3 이하, 7.4, 7.5 생략
7.6 Mutual Information and Correlation
Correlation(상관, 상관관계)는 두 변수 X와 Y 사이의 의존성(dependence)에 대한 통계적 측도(measure)이다. 예를 들어 어떤 사람의 키와 무게는 일반적으로 양의 상관관계가 있다.
상관계수,correlation_coefficient는 ρ(Greek rho)로 표기. 정의는
![$\rho=\frac{{\rm E}[(x_j-\bar{x})(y_j-\bar{y})]}{\sigma_x \sigma_y}$ $\rho=\frac{{\rm E}[(x_j-\bar{x})(y_j-\bar{y})]}{\sigma_x \sigma_y}$](/123/cgi-bin/mimetex.cgi?\Large \rho=\frac{{\rm E}[(x_j-\bar{x})(y_j-\bar{y})]}{\sigma_x \sigma_y})
여기서
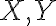 가 각각
가 각각  개 값일 때 상관계수는 이렇게 추정된다(estimated)
개 값일 때 상관계수는 이렇게 추정된다(estimated)
(y_j-\bar{y}))
그림 7.4에서처럼 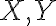 가 가우스분포에서 나온 것이면(drawn from Gaussian distribution), 그리고 correlation ρ이면,
가 가우스분포에서 나온 것이면(drawn from Gaussian distribution), 그리고 correlation ρ이면, 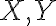 사이 상호정보는 그림 7.5에서처럼
사이 상호정보는 그림 7.5에서처럼
=0.5\log\frac{1}{1-\rho^2} \;\textrm{ bits})
이다. 식을 변형해 I에서 ρ를 얻는 식을 구하면 다음과 같다.
}})
correlation은 상호정보의 special version으로 볼 수 있다.
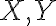 가 큰 상호정보를 갖고, correlation이 0인 것은 가능. (e.g. if they are not Gaussian)
가 큰 상호정보를 갖고, correlation이 0인 것은 가능. (e.g. if they are not Gaussian)
하지만 큰 correlation을 갖고 상호정보가 0인 것은 불가능.
Correlation(상관, 상관관계)는 두 변수 X와 Y 사이의 의존성(dependence)에 대한 통계적 측도(measure)이다. 예를 들어 어떤 사람의 키와 무게는 일반적으로 양의 상관관계가 있다.
상관계수,correlation_coefficient는 ρ(Greek rho)로 표기. 정의는
하지만 큰 correlation을 갖고 상호정보가 0인 것은 불가능.
7.7. The Fixed Range Channel
topics: 엔트로피를 최대화하여 상호정보를 최대화하기, transformed variable의 엔트로피, related variables의 엔트로피, 어떤 encoding function이 엔트로피를 최대화하는가?
topics: 엔트로피를 최대화하여 상호정보를 최대화하기, transformed variable의 엔트로피, related variables의 엔트로피, 어떤 encoding function이 엔트로피를 최대화하는가?
단어/표현 정리
in common with : …과 공동으로
in effect : 사실상 / 실제로는
correlation : 상관, 상관관계
in common with : …과 공동으로
in effect : 사실상 / 실제로는
correlation : 상관, 상관관계

