Contents
- 1. 정보/통신/데이터 과학의 엔트로피
- 1.1. 설명/정의
- 1.2. 관련/관계?
- 1.3. 엔트로피의 고저, 상한/하한
- 1.4. 여러 엔트로피
- 1.5. 결합엔트로피와 조건부엔트로피 (joint and conditional)
- 1.6. 결합엔트로피 joint entropy
- 1.7. 조건부 엔트로피 conditional entropy
- 1.8. (비교 : 교차엔트로피 and 상대엔트로피 / cross entropy and relative entropy)
- 1.9. 교차엔트로피 크로스엔트로피 cross-entropy
- 1.10. 상대엔트로피 relative entropy = Kullback-Leibler divergence = KL-divergence = KLD
- 1.11. 전송 엔트로피?? transfer entropy
- 1.12. 미분엔트로피 differential entropy
- 1.13. Kolmogorov Entropy, metric entropy
- 1.14. Topological Entropy
- 1.15. binary entropy function
- 1.16. 엔트로피의 연쇄법칙 chain rules for entropy
- 1.17. maximum entropy (probability) distribution
- 1.18. (Wikipedia 읽기)
- 1.19. Links ko
- 1.20. links en
- 1.21. Twins (excl. Wikipedia)
- 2. 열역학의 엔트로피
- 3. 둘 다
- 4. 기타, 위로 mv
1. 정보/통신/데이터 과학의 엔트로피 ¶
section 1(여기)은 정보엔트로피,information_entropy(=Shannon_entropy) 로 분리할수도.. (일단은 안 할 확률이 높지만)
TBW: Shannon이 아닌 Hartley_entropy , ... etc
TBW: Shannon이 아닌 Hartley_entropy , ... etc
X, Y가 확률변수일 때
Sub:
| ko | en | 기호/링크 |
| 정보 엔트로피 =Shannon 엔트로피? | entropy | H |
| 주변엔트로피 | marginal entropy | H(X) |
| 결합엔트로피 | joint entropy | H(X,Y) |
| 조건부엔트로피 | conditional entropy | H(X|Y) |
| 교차엔트로피 크로스엔트로피 | cross-entropy | H(X,Y) CHK |
| transfer entropy | ||
| 미분엔트로피 | differential entropy | |
| 상대? 상대적? | relative entropy = KL-divergence = KLD | DKL(XǁY)=H(X,Y)-H(X) CHK |
Sub:
1.1. 설명/정의 ¶
Measure of information in terms of uncertainty.
기호: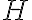 
정의
 "$H=\sum_{i=1}^{n} p_i \log_2\left(\frac{1}{p_i}\right)$")
 "$=-\sum_{i=1}^{n} p_i \log_2(p_i)$")
(Khan Academy)
The entropy of a random variable 
with a 확률질량함수,probability_mass_function,PMF  "$p(x)$")
is defined by
=-\sum_x p(x)\log_2 p(x) "$H(X)=-\sum_x p(x)\log_2 p(x)$")
(밑을 2로 하면 단위는 bit)
The entropy is a measure of the average uncertainty in the random variable. It is the number of bits on average required to describe the random variable.
(Cover Thomas p5)
The entropy is a measure of the average uncertainty in the random variable. It is the number of bits on average required to describe the random variable.
(Cover Thomas p5)
편의상 PMF는
(정의) 이산확률변수 의 엔트로피
=-\sum_{x\in\mathcal{X}}p(x)\log p(x) "$H(X)=-\sum_{x\in\mathcal{X}}p(x)\log p(x)$")
 "$H(p)$")
라고도 쓴다.
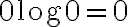관례를 쓴다.  "$(x\to 0\Rightarrow x\log x\to 0)$")
로그의 밑이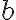
이면, 엔트로피를  "$H_b(X)$")
로 나타낸다.
Note: 엔트로피는 의 분포(see 확률분포,probability_distribution)의 범함수,functional이다. It does not depend on the actual values taken by the random variable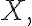 
but only on the probabilities.
로그의 밑이
Note: 엔트로피는
(Remark) 의 엔트로피는 확률변수 } "$\log\frac1{p(X)}$")
의 기대값으로 해석할 수도 있다. ( where is drawn according to pmf )
=E_p\log\frac{1}{p(X)} "$H(X)=E_p\log\frac{1}{p(X)}$")
(Lemma) \ge 0 "$H(X)\ge 0$")
이다.
(Proof)\le 1 "$0\le p(x)\le 1$")
이므로 }\ge 0 "$\log\frac1{p(x)}\ge 0$")
(Proof)
(Lemma) =(\log_b a)H_a(X) "$H_b(X)=(\log_b a)H_a(X)$")
(Proof)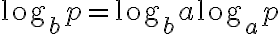
(Proof)
(Cover Thomas p13 2.1 Entropy)
Shannon entropy
=-\sum_x p(x)\log_2 p(x) "$H(x)=-\sum_x p(x)\log_2 p(x)$")
해석:
![[https]](/123/imgs/https.png)
https://data.korea.ac.kr/?p=5453)
- 모든 사건 정보량의 기대값(?)
- 전체 사건,event의 확률분포,probability_distribution의 불확실성,uncertainty의 양을 수치화할 때 사용
- 사건의 확률분포가 균일할수록, 불확실성의 정도가 커지므로, 정보량 즉 엔트로피가 높다.
https://data.korea.ac.kr/?p=5453)tmp from https://untitledtblog.tistory.com/119
{
전체 데이터의 길이가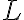
이고, 기호 
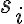로 이루어졌고, 데이터에서 어떤 기호 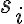가 등장하는 횟수가 
일 때, 어떤 기호가 등장할 확률,probability은
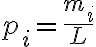
어떤 기호의 정보량(goto 정보,information)은
=\log_2\frac{1}{p_i}=-\log_2p_i "$I(s_i)=\log_2\frac{1}{p_i}=-\log_2p_i$")
엔트로피는
=-\sum_i p_i \log_2 p_i "$H=\sum_i p_i I(s_i)=-\sum_i p_i \log_2 p_i$")
}
{
전체 데이터의 길이가
tmp from https://seing.tistory.com/43
{
확률분포,probability_distribution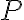
를 갖는
섀넌 엔트로피 "$H(P)$")
는,
전체 사건,event의 확률분포의 불확실성,uncertainty의 양을 나타내며,
모든 사건 정보량의 기대값,expected_value을 뜻한다.
{
확률분포,probability_distribution
섀넌 엔트로피
전체 사건,event의 확률분포의 불확실성,uncertainty의 양을 나타내며,
모든 사건 정보량의 기대값,expected_value을 뜻한다.
수식으로 나타내면,
![$H(P)=H(x)=E_{X\sim P}[I(X)]=-E_{X\sim P}[\log P(x)]$](/123/cgi-bin/mimetex.cgi?\Large H(P)=H(x)=E_{X\sim P}[I(X)]=-E_{X\sim P}[\log P(x)] "$H(P)=H(x)=E_{X\sim P}[I(X)]=-E_{X\sim P}[\log P(x)]$")
=-\sum_{k=1}^{K} p(X=k)\log p(X=k) "$H(X)=-\sum_{k=1}^{K} p(X=k)\log p(X=k)$")
동전던지기 같은 binary 경우를 생각했을 때(베르누이_시행,Bernoulli_trial)
만약=p "$P(X=1)=p$")
이면 =1-p "$P(X=0)=1-p$")
이고
의 엔트로피는
=-p\log_2 p-(1-p)\log_2(1-p) "$H(X)=-p\log_2 p-(1-p)\log_2(1-p)$")
앞면이 나오는 경우 50%의 확률 =0.5 "$P(X=1)=0.5$")
뒷면이 나오는 경우 50%의 확률=0.5 "$P(X=0)=0.5$")
따라서 동전던지기의 엔트로피는
![$-[p(X=0)\log_2 p(X=0)+p(X=1)\log_2 p(X=1)]$](/123/cgi-bin/mimetex.cgi?\Large -[p(X=0)\log_2 p(X=0)+p(X=1)\log_2 p(X=1)] "$-[p(X=0)\log_2 p(X=0)+p(X=1)\log_2 p(X=1)]$")
![$=-[0.5\log_2 0.5 + 0.5 \log_2 0.5]$](/123/cgi-bin/mimetex.cgi?\Large =-[0.5\log_2 0.5 + 0.5 \log_2 0.5] "$=-[0.5\log_2 0.5 + 0.5 \log_2 0.5]$")
![$=-[(0.5\times -1)\times 2]$](/123/cgi-bin/mimetex.cgi?\Large =-[(0.5\times -1)\times 2] "$=-[(0.5\times -1)\times 2]$")
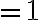
Binary entropy function:
// binary_entropy_function
}
만약
뒷면이 나오는 경우 50%의 확률
따라서 동전던지기의 엔트로피는
// binary_entropy_function
}
(2021-07-15)
정보 엔트로피 = 섀넌 엔트로피 = 평균 정보량.
이산확률변수,discrete_random_variable 의 표본공간,sample_space이 
일 때 정보 엔트로피는
![$H(X)=E[I(X)]=-\sum_{i=1}^n P(x_i) \log_b(P(x_i))$](/123/cgi-bin/mimetex.cgi?\Large H(X)=E[I(X)]=-\sum_{i=1}^n P(x_i) \log_b(P(x_i)) "$H(X)=E[I(X)]=-\sum_{i=1}^n P(x_i) \log_b(P(x_i))$")
from https://angeloyeo.github.io/2020/10/26/information_entropy.html
이산확률변수,discrete_random_variable
정보량의 기대값.
사건을 표현하기 위해 요구되는 평균 자원.
i.e.
확률적으로 발생하는 사건,event에 대한 정보량(see 정보,information)의 (평균,mean,average 혹은 기대값,expected_value).
사건을 표현하기 위해 요구되는 평균 자원.
i.e.
확률적으로 발생하는 사건,event에 대한 정보량(see 정보,information)의 (평균,mean,average 혹은 기대값,expected_value).
tmp from https://hoya012.github.io/blog/cross_entropy_vs_kl_divergence/
{
특정한 stochastic process에서 생성된 정보의 평균.
정보의 기대값.
![$H(X)=E[I(X)]=E[-\log(P(X))]=-\sum_{i=1}^{n} P(x_i)\log P(x_i)$](/123/cgi-bin/mimetex.cgi?\Large H(X)=E[I(X)]=E[-\log(P(X))]=-\sum_{i=1}^{n} P(x_i)\log P(x_i) "$H(X)=E[I(X)]=E[-\log(P(X))]=-\sum_{i=1}^{n} P(x_i)\log P(x_i)$")
}
{
특정한 stochastic process에서 생성된 정보의 평균.
정보의 기대값.
tmp from https://kyoko0825.tistory.com/entry/이론-Entropy
{
무작위 사건의 결과, 또는 확률변수에 대한 불확실성을 포함하는 정보의 양.
엔트로피 높음 : 불확실성 커짐
엔트로피 작음 : 불확실성 작음
}
{
무작위 사건의 결과, 또는 확률변수에 대한 불확실성을 포함하는 정보의 양.
엔트로피 높음 : 불확실성 커짐
엔트로피 작음 : 불확실성 작음
}
1.2. 관련/관계? ¶
다음은 엔트로피와 비교/비유됨, 관계 정확히 서술 TBW
- 답을 알기까지 필요한 질문의 수
- unpredictability 예측불가능성 ... 즉 예측가능하면, 너무 뻔하면 vs 드물면 or 예측이 불가능하면, ... // 예측,prediction
- uncertainty 불확실성
- disorder 무질서
- = 비손실 정보 압축의 한계?
1.3. 엔트로피의 고저, 상한/하한 ¶
| 엔트로피가 낮다 | 엔트로피가 높다 |
| 예측하기 쉬움 | 예측하기 어려움 |
| 확실한 정보 | 놀라운 정보 |
엔트로피 하한값(최소) :
모든 심볼 중 하나의 발생확률이 1이고 나머지 발생확률이 0
불확실성이 없음
엔트로피 상한값(최대) : 불확실성이 없음
모든 심볼이 동일한 발생확률
불확실성이 최대
from 불확실성이 최대
![[http]](/123/imgs/http.png)
ktword 엔트로피| surprise | entropy |
| minimum surprise | 0 |
1.4. 여러 엔트로피 ¶
marginal entropy
,\,H(Y) "$H(X),\,H(Y)$")
conditional entropy
joint entropy
cross entropy
differential entropy
relative entropy = KL divergence = KL-divergence = KLD
joint entropy
cross entropy
differential entropy
relative entropy = KL divergence = KL-divergence = KLD
1.10. 상대엔트로피 relative entropy = Kullback-Leibler divergence = KL-divergence = KLD ¶
두 확률분포,probability_distribution의 유사성(similarity)을 정의하기 위해 쓰이는 방법 중 하나.
Not commutative. (교환법칙,commutativity X)
항상 0 이상.
Not commutative. (교환법칙,commutativity X)
항상 0 이상.
이산분포 P, Q일 때
![$D_{KL}(P\mid\mid Q)=\sum_i P[i]\log\frac{P[i]}{Q[i]}$](/123/cgi-bin/mimetex.cgi?\Large D_{KL}(P\mid\mid Q)=\sum_i P[i]\log\frac{P[i]}{Q[i]} "$D_{KL}(P\mid\mid Q)=\sum_i P[i]\log\frac{P[i]}{Q[i]}$")
연속분포 p, q일 때
=\int_{-\infty}^{\infty}p(x)\log\frac{p(x)}{q(x)}dx "$D_{KL}(P\mid\mid Q)=\int_{-\infty}^{\infty}p(x)\log\frac{p(x)}{q(x)}dx$")
tmp bmks ko
KLD와 JSD(Jensen-Shannon_divergence)
https://hyeongminlee.github.io/post/prob002_kld_jsd/
KLD와 JSD(Jensen-Shannon_divergence)
https://hyeongminlee.github.io/post/prob002_kld_jsd/
// tmp from https://blog.naver.com/towo222/222295696840
https://mathworld.wolfram.com/RelativeEntropy.html
AI 용어사전: KL-divergence
aka Kullback-Leibler distance
http://biohackers.net/wiki/RelativeEntropyAI 용어사전: KL-divergence1.13. Kolmogorov Entropy, metric entropy ¶
Kolmogorov entropy, Kolmogorov-Sinai entropy, or KS entropy
1.17. maximum entropy (probability) distribution ¶
pagename tbd:
maximum_entropy_probability_distribution
or
maximum_entropy_distribution
maximum_entropy_probability_distribution
or
maximum_entropy_distribution
1.18. (Wikipedia 읽기) ¶
from 
Entropy_(information_theory)
{
information content (aka surprisal) of an event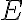
는 확률,probability "$p(E)$")
와 관계가
=-\log_2(p(E))=\log_2(1/p(E)) "$I(E)=-\log_2(p(E))=\log_2(1/p(E))$")
확률변수,random_variable
가능한 값
확률질량함수,probability_mass_function,PMF "$P(X)$")
일 때,
엔트로피,entropy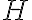 는 이렇게 정의된다.
![$H(X)=E[I(X)]=E[-\log(P(X))]$](/123/cgi-bin/mimetex.cgi?\Large H(X)=E[I(X)]=E[-\log(P(X))] "$H(X)=E[I(X)]=E[-\log(P(X))]$")
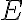: 기대값,expected_value 연산자
: information content (정보,information)
Entropy_(information_theory){
| I | information content |
| H | entropy |
information content (aka surprisal) of an event
는 확률,probability
가능한 값
확률질량함수,probability_mass_function,PMF
일 때,
엔트로피,entropy
}
............TODO MERGE.........
확률변수,random_variable의 엔트로피는, the average level of '정보', '놀라움', or '불확실성' inherent in the variable's possible 결과,outcomes.
Given a 이산확률변수,discrete_random_variable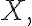
with possible 결과,outcomes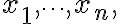
which occur with 확률,probability,\cdots,\textrm{P}(x_n), "$\textrm{P}(x_1),\cdots,\textrm{P}(x_n),$")
the entropy of is formally defined as:
=-\sum_{i=1}^{n} \textrm{P}(x_i) \log \textrm{P}(x_i) "$\textrm{H}(X)=-\sum_{i=1}^{n} \textrm{P}(x_i) \log \textrm{P}(x_i)$")
log의 base가
An equivalent definition of entropy is the expected value of the self-information of a variable.
with possible 결과,outcomes
which occur with 확률,probability
the entropy of
2 : bit, shannon
e : nat
10 : dit, ban, hartley
동등한 다른 정의:e : nat
10 : dit, ban, hartley
An equivalent definition of entropy is the expected value of the self-information of a variable.
사건,event 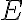에 대해, information content (또는 surprisal)은 확률 가 증가할수록 감소한다. 수식으로는
주사위 던지기 결과가 동전 던지기 결과보다 엔트로피가 높다. 확률 1/6이 1/2보다 적으므로.
1.19. Links ko ¶
정보량, 엔트로피(Entropy), 결합 엔트로피(Joint Entropy), 조건부 엔트로피(Conditional Entropy), 상호 정보량(Mutual Information), Transfer Entropy를 정리한 곳
https://mons1220.tistory.com/128
https://mons1220.tistory.com/128
https://hyunw.kim/blog/2017/10/14/Entropy.html
https://hyunw.kim/blog/2017/10/26/Cross_Entropy.html
https://hyunw.kim/blog/2017/10/26/Cross_Entropy.html
로지스틱회귀,logistic_regression의 비용함수,cost_function는 cross entropy 식과 같다. (Cross entropy는 log loss로 불리기도 하는데, 왜냐하면 cross entropy를 최소화하는 것은 log likelihood를 최대화하는 것과 같기 때문.)
https://hyunw.kim/blog/2017/10/27/KL_divergence.html2. 열역학의 엔트로피 ¶
기호 S
무질서도. - 이건 너무 단순화된 설명이라고 어디서 본 듯 한데..
가역반응에서 교환된 열의 비율.
에너지의 질(quality).
영어의 spread(ness)에서 왔다는데...
다른 곳에선 Claude Shannon에서 왔다는데... CHK
The measure of chaos or disorder in a system.다른 곳에선 Claude Shannon에서 왔다는데... CHK
무질서도. - 이건 너무 단순화된 설명이라고 어디서 본 듯 한데..
가역반응에서 교환된 열의 비율.
에너지의 질(quality).
엔트로피가 낮은 에너지는 양질의 에너지
엔트로피가 높으면 질이 낮은 에너지
계의 무질서한 정도를 나타내는 상태함수. 엔트로피가 높으면 질이 낮은 에너지
계의 에너지를 분배하는 방법의 수
입자의 운동 자유도,degree_of_freedom 및 입자를 배열하는 방법의 수와 밀접하게 연관된 열역학적 변수
계,system는 더 낮은 엔탈피,enthalpy와 더 높은 엔트로피를 가지려는 경향이 있음
// https://youtu.be/LzNawB4Pbu8 17m
입자의 운동 자유도,degree_of_freedom 및 입자를 배열하는 방법의 수와 밀접하게 연관된 열역학적 변수
계,system는 더 낮은 엔탈피,enthalpy와 더 높은 엔트로피를 가지려는 경향이 있음
// https://youtu.be/LzNawB4Pbu8 17m
상태(P, V)에 대한 함수이다. S(P, V)
S = kB ln Ω
엔트로피 = 볼츠만_상수,Boltzmann_constant × ln(계의 가능한 상태 수)
단위 J K-1
엔트로피의 증가감소 and 열역학법칙은 공간,space까지 따져봐야 됨.
엔트로피는 어디서나 항상 증가한다고 생각하면 안됨.
우주 전체에서는 항상 증가. 다만 국소적으로(locally) 감소 가능.
}
엔트로피는 어디서나 항상 증가한다고 생각하면 안됨.
우주 전체에서는 항상 증가. 다만 국소적으로(locally) 감소 가능.
}
ebs 장인수: 볼츠만의 표현
볼츠만의 엔트로피 방정식
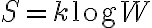
볼츠만의 엔트로피 방정식
- 경우의 수가 많을수록 엔트로피 증가
2.1. 엔트로피의 변화, 그 세 종류 ¶
엔트로피의 변화가 중요
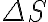
세가지?? CHK. sys=system=계, surr=surroundings=주위, univ=universe=우주.
ΔS계 + ΔS주위 = ΔS우주
| ΔS계 | |
| ΔS주위 | |
| ΔS우주 |
ΔS계 + ΔS주위 = ΔS우주
2.2. Links ¶
에너지,energy와의 관계:
어떤 계,system가 가진 에너지는 (사용가능한에너지)와 (사용불가능한에너지)로 구분가능.
(사용가능한에너지)는 그 계가 외부에 일,work을 하는 데 사용될 수 있음.
(사용불가능한에너지)는 존재는 해도 그 계가 외부에 일을 하는 데 사용될 수 없음.
엔트로피는 (사용불가능한에너지)와 관계가 있지만, 에너지는 아님.
엔트로피의 단위는 에너지를 온도로 나눈 J/K. i.e. 에너지와 차원이 다름.
어떤 계,system가 가진 에너지는 (사용가능한에너지)와 (사용불가능한에너지)로 구분가능.
(사용가능한에너지)는 그 계가 외부에 일,work을 하는 데 사용될 수 있음.
(사용불가능한에너지)는 존재는 해도 그 계가 외부에 일을 하는 데 사용될 수 없음.
엔트로피는 (사용불가능한에너지)와 관계가 있지만, 에너지는 아님.
엔트로피의 단위는 에너지를 온도로 나눈 J/K. i.e. 에너지와 차원이 다름.
열역학제이법칙에 따르면 엔트로피는 줄어들지 않음.
엔트로피 정의 방법
크게 열역학적 방법과 통계역학적 방법 두 가지.
그럼 통계역학적 정의를 하려면 앙상블,ensemble(어떤 계가 가질 수 있는 미시상태,microstate의 모임)을 먼저 도입.
미시 상태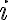
의 확률을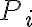 
라 하면, 주어진 앙상블의 엔트로피는 (정의)
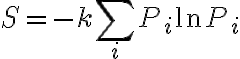
여기서 
는 볼츠만_상수,Boltzmann_constant.
고립계,isolated_system의 경우 모든 미시상태,microstate가 동일한 확률을 갖는다고 가정하면
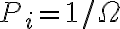
여기서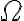 
: 가능한 모든 미시상태의 개수. 그러면,
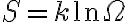
열저장체(heat reservoir)와 열적 평형을 이룬 계의 미시상태는 볼츠만_분포(curr see 볼츠만_상수,Boltzmann_constant)
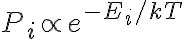
를 따르며, 이 확률분포,probability_distribution를 엔트로피 정의에 대입하면
) "$S=k\frac{\partial}{\partial T}(T\ln Z(T))$")
이고, 여기서
=\sum_i e^{-E_i/kT} "$Z(T)=\sum_i e^{-E_i/kT}$")
는 분배함수,partition_function.
}
크게 열역학적 방법과 통계역학적 방법 두 가지.
| 정의 방법 | 특성 | 한계1 | 한계2 |
| 열역학적 | 역사적으로 먼저 | 엔트로피의 절대값(절대적인 변화 값???) 정의 불가, 상대적 변화만 정의 가능 | 열역학적 평형 상태인 계에서만 정의 가능 |
| 통계역학적 | 엄밀하고 근본적 | 절댓값정의가능하단다. | 모든 계에 정의 가능 |
그럼 통계역학적 정의를 하려면 앙상블,ensemble(어떤 계가 가질 수 있는 미시상태,microstate의 모임)을 먼저 도입.
미시 상태
고립계,isolated_system의 경우 모든 미시상태,microstate가 동일한 확률을 갖는다고 가정하면
}
