See also 아날로그회로,analog_circuit - merge?
1. Basics ¶
Pavg = 1/2 × (Ppeak)
(Average power = 1/2 × Peak power)
i.e.
Pavg = Ppeak / 2 … ①
(Average power = 1/2 × Peak power)
i.e.
Pavg = Ppeak / 2 … ①
Ppeak = Vpeak × Ipeak … ②
Vpeak = Ipeak × R
Ipeak = Vpeak / R … ③
Ipeak = Vpeak / R … ③
②, ③에서
Ppeak = (Vpeak2) / R … ④
또한
Ppeak = Ipeak2 × R … ⑤
Ppeak = (Vpeak2) / R … ④
또한
Ppeak = Ipeak2 × R … ⑤
①, ④에서
Pavg = (Vpeak2) / (2R)
Pavg = (Vpeak2) / (2R)
①, ⑤에서
Pavg = (Ipeak2 × R) / 2
Pavg = (Ipeak2 × R) / 2
그래서 회로의 전력,power은
AC circuit과 DC circuit을 비교하고 두 회로의 power가 같다고 가정하면
위 표의 왼쪽 column에서 (두 P가 같다고 가정)
| P = V2 / R | P = I2 R | |
| DC circuit | P = VDC2 / R | P = IDC2 R |
| AC circuit | Pavg = (Vpeak2) / (2R) | Pavg = (Ipeak2 × R) / 2 |
AC circuit과 DC circuit을 비교하고 두 회로의 power가 같다고 가정하면
위 표의 왼쪽 column에서 (두 P가 같다고 가정)
(VDC2) / R = (Vpeak2) / (2R) 이므로
VDC = (Vpeak) / √2
오른쪽 column에서 (두 P가 같다고 가정)VDC = (Vpeak) / √2
IDC2 R = (Ipeak2 × R) / 2 이므로
IDC = Ipeak / √2
이 두 결과는 RMS관련? — (DC회로의 voltage, current의 RMS값 ↔ AC회로의 peak값)은 이런 관계. chkIDC = Ipeak / √2
VRMS = (Vpeak) / √2
IRMS = Ipeak / √2
IRMS = Ipeak / √2
3. L이 있는 교류회로 ¶
유도계수(인덕턴스,inductance) L인 유도기,inductor(코일)이 있는 회로에 교류가 흐르면 코일을 지나는 자속,magnetic_flux이 주기적으로 변한다. 그러면 자속 변화를 방해하는 방향으로 역기전력,counter_emf이 생겨서 전류의 흐름을 방해함.
최대 전압일 때 전류는 0이 됨.
전압의 위상이 전류의 위상보다 90˚( 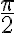 ) 앞섬.
) 앞섬.
역기전력의 크기는 코일의 L과 주파수 f에 비례.
유도성리액턴스를 써서 옴_법칙,Ohm_law을 나타내면,
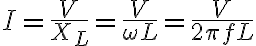
L이 교류 흐름을 방해하지만, R 교류회로와 달리 전력,power을 소비하지 않음. 자기장 에너지로 저장되었다가 다시 복귀.
Vrms = Irms XL
XC = ω L
XC = ω L
Inductive reactance 리액턴스,reactance (XL)과 frequency(f)는 비례
높은 frequency에서
I(t) = I0 sin(ωt - π/2)
=L\frac{\Delta I}{\Delta t})
\Delta t)
\Delta t)
\Delta(\omega t))
)
)
높은 frequency에서
- XL은 증가
- 전류는 감소
I(t) = I0 sin(ωt - π/2)
4. C가 있는 교류회로 ¶
C가 최대로 충전된 순간 전압은 최대가 되고 전류는 0이 됨.
C가 충전되지 않은, 즉 전압이 0일 때 전류는 최대가 됨.
C가 충전되지 않은, 즉 전압이 0일 때 전류는 최대가 됨.
전압의 위상이 전류보다 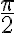 만큼 늦어짐.
만큼 늦어짐.
교류에 대한 저항을 용량리액턴스,capacitive_reactance(XC)라 하며
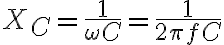 (단위 Ω)
(단위 Ω)
XC를 써서 옴의 법칙을 나타내면
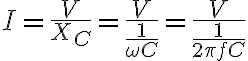
R 교류회로와 달리 전력,power을 소비하지 않음. 에너지가 전기장,electric_field에 저장되었다가 다시 복귀하기 때문.
Capacitive reactance 리액턴스,reactance (XC, 단위 ohms)는 frequency(f, 단위 Hz)와 반비례
Vrms = Irms XC
XC = 1/(ωC)
Vrms = Irms XC
XC = 1/(ωC)
주파수가 커지면:
I(t) = I0 sin(ωt + π/2)
Q(t) = C V0 sin(ωt)
=\frac{\Delta Q}{\Delta t}=\omega CV_0 \cos (\omega t))
}\sin\left(\omega t+\frac{\pi}{2}\right))
- XC는 감소
- 전류는 증가
I(t) = I0 sin(ωt + π/2)
Q(t) = C V0 sin(ωt)

