교류 전류, alternating current, AC, ac
1. head ¶
교류의 정의가 제각각인데 DC가 아니면 다 AC인가? 이건 확실히 아닌 듯 하고
시간에 따라 변하는 전류(time-varying current) 중 흔한 형태(common form)는 사인/코사인 형태를 띠는(sinusoidal) 전류.
교류(ac)란 시간에 대해 sinusoidally 변하는 전류. (a current that varies sinusoidally with time) (Alexander/Sadiku)
시간에 따라 변하는 전류(time-varying current) 중 흔한 형태(common form)는 사인/코사인 형태를 띠는(sinusoidal) 전류.
교류(ac)란 시간에 대해 sinusoidally 변하는 전류. (a current that varies sinusoidally with time) (Alexander/Sadiku)
전류,electric_current에는 직류(DC)와 교류(AC)가 있음
직류,DC의 저항,resistance에 해당하는 게 교류에 여러가지가 있는데...
= 교류회로의 저항.................
Related:
공급되는(전원,source) 변하는(AC) 전압(ACV = AC voltage)을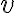 라 하고
라 하고
그 외에?
직류는 시간,time이 흘러도 일정하지만, 교류는 이러한 시간 성질이 있음직류,DC의 저항,resistance에 해당하는 게 교류에 여러가지가 있는데...
TOWRITE
{= 교류회로의 저항.................
Related:
공급되는(전원,source) 변하는(AC) 전압(ACV = AC voltage)을
= 교류회로의 인덕터 ..............
위상자,phasor diagram상에선 ΔvL이 iL보다 90도 먼저/빨리/앞섬? CHK
= 교류회로에서의 축전기.........................
C 양단의 전위차는
KVL에 의해
V=IR, I=V/R과 비교하면, 위 식에서 저항 역할을 하는 것은
즉 교류C회로의 저항에 해당하는 것이
명칭과 기호는 리액턴스,reactance X > 용량리액턴스,capacitive_reactance XC
iC가 Δvc보다 90도 빠르다
Δvc가 iC 보다 90도 느리다
Δvc가 iC 보다 90도 느리다
| L회로 | v가 더 빠르다 |
| C회로 | i가 v보다 빠르다 |
= 교류회로에서의 RLC ...............................
RLC 직렬 연결을 가정
즉 전류가 일정: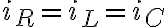
즉 전류가 일정:
R에서의 전위차 ΔvR i.e. R에 걸리는 전압
L에서의 전위차 ΔvL i.e. L에 걸리는 전압
C에서의 전위차 ΔvC i.e. C에 걸리는 전압
)
임의의 시간 t에서
)
L에서의 전위차 ΔvL i.e. L에 걸리는 전압
C에서의 전위차 ΔvC i.e. C에 걸리는 전압
임의의 시간 t에서
i를 고정시키고 ![$\Delta v_{[R,L,C]}$ $\Delta v_{[R,L,C]}$](/123/cgi-bin/mimetex.cgi?\Large \Delta v_{[R,L,C]}) 를 구하면
를 구하면
(t에 대해 어떻게 변하는지 본다면)

(t에 대해 어떻게 변하는지 본다면)

L과 C가 없어지면 저항은 Z=R, 교류회로는 직류회로와 똑같아짐을 볼 수 있다.
실용적으로 다음이 중요:
임피던스 감소 (열손실을 줄이기 위해) - 각진동수를 적절히 조절해서
임피던스 매칭 (교환손실을 줄이기 위해)
임피던스 감소 (열손실을 줄이기 위해) - 각진동수를 적절히 조절해서
임피던스 매칭 (교환손실을 줄이기 위해)
아울러 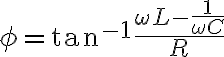
}
2. 교류와 인덕터/인덕턴스의 관계 ¶
인덕터(코일)은,
직류,DC일 때는 그냥 도선으로 작용한다. 하지만
교류일 때는 저항(저항기,resistor)처럼 작용한다.
전류가 변할 때 마다 그 변화를 방해하는 역기전력(see 유도기전력,induced_emf)이 생겨서 전류 흐름을 방해한다.
직류,DC일 때는 그냥 도선으로 작용한다. 하지만
교류일 때는 저항(저항기,resistor)처럼 작용한다.
전류가 변할 때 마다 그 변화를 방해하는 역기전력(see 유도기전력,induced_emf)이 생겨서 전류 흐름을 방해한다.
3. 교류와 커패시터/커패시턴스의 관계 ¶
축전기는 도선의 일부가 끊어진 것과 같으므로
직류일 때는 전류가 흐르지 않는다. 하지만
교류일 때는 커패시터의 극에 충/방전이 반복되어서 전류가 흐르는 효과가 나타난다.
직류일 때는 전류가 흐르지 않는다. 하지만
교류일 때는 커패시터의 극에 충/방전이 반복되어서 전류가 흐르는 효과가 나타난다.
4. ? ¶
5. 최대 평균 실효 등등 ¶
순시값/최대값/피크-피크 값
이것은 교류의 전압/전류/(또 있는지?)의 여러 종류의 값,value들인데,
일단 교류는 매 순간 변하며 각 순간의 값을 순시값(순싯값, instantaneous value)이라고 하고,
순시값 중 가장 큰 값을 최대값(최댓값, maximum value)이라고 하며,
파형에서 양의 최대값과 음의 최대값 사이의 값을 피크-피크 값(peak-to-peak value)이라 한다.
일단 교류는 매 순간 변하며 각 순간의 값을 순시값(순싯값, instantaneous value)이라고 하고,
순시값 중 가장 큰 값을 최대값(최댓값, maximum value)이라고 하며,
파형에서 양의 최대값과 음의 최대값 사이의 값을 피크-피크 값(peak-to-peak value)이라 한다.
ex.
전압의 피크-피크 값: Vp-p
전류의 순시값: i
전류의 최대값: Im
전류의 피크-피크 값: Ip-p
전압의 피크-피크 값: Vp-p
전류의 순시값: i
전류의 최대값: Im
전류의 피크-피크 값: Ip-p
평균값
TBW
TBW
실효값(실횻값, effective value)
TBW
TBW
CHK
{
최대값이 일 때,
일 때,
{
최대값이
순시값 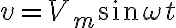
평균값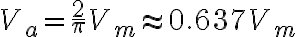
실효값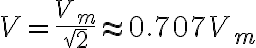
}
평균값
실효값
}
최대값(maximum or peak value)
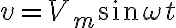
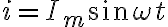
최대 전압: Vm
최대 전류: Im
Peak 간 전압: Vp-p = 2 Vm
Peak-to-peak current: Ip-p = 2 Im
순시값최대 전류: Im
Peak 간 전압: Vp-p = 2 Vm
Peak-to-peak current: Ip-p = 2 Im
평균값 (정현파 교류의)
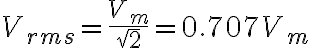
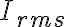
정현파 교류 파형,waveform의 상호관계식
평균전압 = 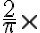 최대전압
최대전압
평균전류 =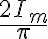
실효값 (root mean square value, see 제곱평균제곱근,root_mean_square,RMS)평균전류 =
| 실효값 | ||
| 평균값 | ||
| 최대값 | ||
| 피크간 값 |
7.1. R만있는회로 ¶
V,I의 위상이 같다, 다만 전류는 전압보다 1/R만큼 진폭이 줄어든 상태
from 백승원 강의자료{
퍼텐셜차
}
7.2. L만있는회로 ¶
코일속의자속이 주기적으로 변함 -> 코일에 역기전력(see 유도기전력,induced_emf)이 발생
V의 위상이 I 위상보다 90°앞섬
역기전력의 크기는, 코일의 자체유도계수 L과 교류전원 주파수 f에 비례
그래서 교류저항은 ωL -> 유도리액턴스,inductive_reactance
V의 위상이 I 위상보다 90°앞섬
역기전력의 크기는, 코일의 자체유도계수 L과 교류전원 주파수 f에 비례
그래서 교류저항은 ωL -> 유도리액턴스,inductive_reactance
XL = ωL = 2πfL
옴의 법칙을 나타내면
from 백승원
{
퍼텐셜차
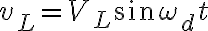
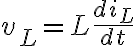
전류
\sin(\omega_d t-90\textdegree))
)
유도형 반응저항
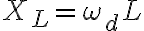
위상상수
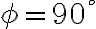
전류가 퍼텐셜차보다 90도 뒤쳐진다.
}
{
퍼텐셜차
}
7.3. C만있는회로 ¶
축전/방전이 번갈아 되풀이
XC = 1/(ωC) = 1/(2πfC)i.e.
from 백승원
{
용량형 회로
{
용량형 회로
퍼텐셜차
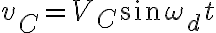
전하

전류
\sin(\omega_d t+90\textdegree))
)
용량형 반응저항
위상상수
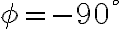
전류가 퍼텐셜차보다 90도 앞선다
}
전류가 퍼텐셜차보다 90도 앞선다
7.5. LC 진동 회로 ¶
축전기의 전기장 에너지 UE
코일의 자기장 에너지 UB가 번갈아가며 전환되면서 총합 유지
용수철_진자,spring_pendulum의 운동에너지
위치에너지가 번갈아가며 유지되는 역학적에너지보존법칙과 유사
코일의 자기장 에너지 UB가 번갈아가며 전환되면서 총합 유지
용수철_진자,spring_pendulum의 운동에너지
위치에너지가 번갈아가며 유지되는 역학적에너지보존법칙과 유사
8. 발전기,generator ¶
영구자석 사이 자기장 B가 걸린 곳에 단면적 A, 감은 수 n인 코일이 회전각속도 ω로 돎
코일 면이 자기장과 수직이 되면 코일을 지나는 자속 Φ는
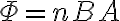
회전하면 코일 면이 기울어지므로 코일 면을 지나는 자속 Φ는
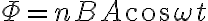
자속의 시간변화율은
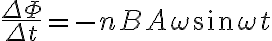
코일의 양 끝에 걸리는 유도기전력,induced_emf V는
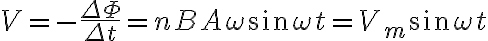
(V = 유도 기전력의 순간값, Vm = 유도 기전력의 최대값)
V와 I의 파형은 똑같음
코일 면이 자기장과 수직이 되면 코일을 지나는 자속 Φ는
(V = 유도 기전력의 순간값, Vm = 유도 기전력의 최대값)


![[http]](/123/imgs/http.png)
![[https]](/123/imgs/https.png)