기호 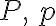
단위 W (watt)
Energy per unit time
(이건 부호를 고려하지 않은 서술인가? 아님 음의 에너지,energy/일,work을 잘 정의하면 해결되는 문제인가? CHK)
단위 W (watt)
1 W = 1 V · A (P = V I 에서)
1 W = 1 J/s (P = W/t 에서)
단위시간,time당 에너지,energy1 W = 1 J/s (P = W/t 에서)
Energy per unit time
(이건 부호를 고려하지 않은 서술인가? 아님 음의 에너지,energy/일,work을 잘 정의하면 해결되는 문제인가? CHK)
단위시간당 공급되거나 흡수되는 에너지.
관계식
전력 = 일률 = 일 / 시간
(전력보다는 일률 명칭에서 관계를 쉽게 유추 가능)
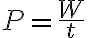
또는 (전력보다는 일률 명칭에서 관계를 쉽게 유추 가능)
전력 = d일 / d시간
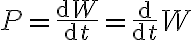
기호
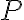 : 시간에 따라 변하지 않는 전력
: 시간에 따라 변하지 않는 전력
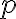 : 시간에 따라 변하는 전력
: 시간에 따라 변하는 전력
정의
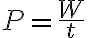
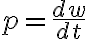
단위
1 W = 1 J / 1 s (watt = joule/second)
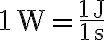
3. 교류,AC에서 ¶
순시전력 = (일의 변화율) / (시간 변화율)
1 W = 1 J/s
순시전력 = 순시전압 · 순시전류 - ? CHK
P = V I
1W = 1V·A
1W = 1V·A
(같은 내용인데 좀 다르게 써 보면)
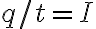 이므로
이므로
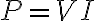
저항기,resistor의 전력 손실(power loss in a resistor)
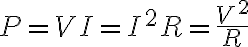
초당 저항기의 열 발생 (thermal energy generated in a resistor per second)도 power loss와 마찬가지
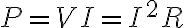
(너무 뻔한가. 근데 여기는 마지막 식은 삭제되어 있는데 왜지) DELME
power = work / time
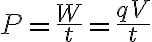
그런데 (Schaum College Phy: Electrical Power)
고딩
P
= I V
= I2 R (전류가 일정할 때)
= V2 / R (전압이 일정할 때)
회로에서 전구의 밝기는 전력에 비례.= I2 R (전류가 일정할 때)
= V2 / R (전압이 일정할 때)
220V제품을 110V에 연결하면, 전력은
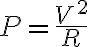
에 의해 정격전력의 1/4만 공급됨.
발전소에서 가정으로 송전할 때, 송전선에서 손실되는 에너지 계산은 (전압의 제곱에 반비례하는 그것) 이렇게 함.
Phome = 가정 사용 전력
Pwasted = 송전선에서 손실되는 전력
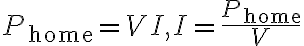
이므로
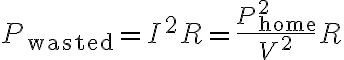
근데 왜 P에 대한 서로 다른 두 식을 쓰는건지? 왜 가정 식은 저거고 송전선 식은 저거임???
Phome = 가정 사용 전력
Pwasted = 송전선에서 손실되는 전력
4. topics ¶
순시 전력(instantaneous power)
평균 전력(average power) (=유효전력(real power) CHK)
복소전력,complex_power S
피상전력,apparent_power
유효전력,active_power
무효전력,reactive_power
피상전력²=유효전력²+무효전력² CHK - yes
{
유효전력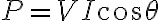
무효전력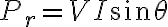
피상전력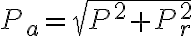
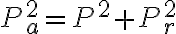

평균 전력(average power) (=유효전력(real power) CHK)
복소전력,complex_power S
유효전력+무효전력? chk
피상전력(apparent power) Pa피상전력,apparent_power
단위VA,kVA
: 복소전력의 크기, AC의 power나 load를 표시, VI CHK
교류의 부하나 전원의 용량을 나타내는 데 사용하는 값. 겉보기 전력이라고도 함.
단위: VA (볼트암페어)
유효전력(real power, active power) P: 복소전력의 크기, AC의 power나 load를 표시, VI CHK
교류의 부하나 전원의 용량을 나타내는 데 사용하는 값. 겉보기 전력이라고도 함.
단위: VA (볼트암페어)
유효전력,active_power
단위W,kW
: 기기의 작동에 실제 도움이 되는 전력, 저항에서 소비되는 전력, VIcosθ CHK
부하에 유도기,inductor와 축전기,capacitor 성분이 포함되어 있는 경우 전압과 전류 사이에 위상차,phase_difference가 발생하여 회로소자에서 소비되는 전력.
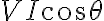
단위: W
무효전력(reactive power) Q: 기기의 작동에 실제 도움이 되는 전력, 저항에서 소비되는 전력, VIcosθ CHK
부하에 유도기,inductor와 축전기,capacitor 성분이 포함되어 있는 경우 전압과 전류 사이에 위상차,phase_difference가 발생하여 회로소자에서 소비되는 전력.
단위: W
무효전력,reactive_power
단위Var,kVar,VAR?
: 부하에서 소비되지 않고 L,C에 축적되었다가 방출?, 실제로 아무 일을 하지 않는 전력, VIsinθ CHK
회로 소자에서 소비되지 않고 저장되었다가 전원 측으로 회수되는 전력.
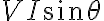
단위: Var
역율(power factor) 역률,power_factor pf: 부하에서 소비되지 않고 L,C에 축적되었다가 방출?, 실제로 아무 일을 하지 않는 전력, VIsinθ CHK
회로 소자에서 소비되지 않고 저장되었다가 전원 측으로 회수되는 전력.
단위: Var
피상전력²=유효전력²+무효전력² CHK - yes
{
유효전력
무효전력
피상전력

역률:
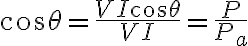
무효율:
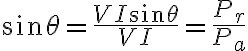
}
위상각,phase_angle = 역률각(power factor angle)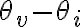 CHK
CHK
TODO http://www.ktword.co.kr/abbr_view.php?m_temp1=4091 보고 정리
위상각,phase_angle = 역률각(power factor angle)
TODO http://www.ktword.co.kr/abbr_view.php?m_temp1=4091 보고 정리
5. 피상전력/유효전력/무효전력 ¶
CHK
{
교류회로에서 전력은, 유도성 부하에 공급된 전압과 전류 사이에 위상차,phase_difference가 있을 때
}
{
교류회로에서 전력은, 유도성 부하에 공급된 전압과 전류 사이에 위상차,phase_difference가 있을 때
- 부하에서 소비되는 유효전력,active_power과
- 부하에서 소비되지 않고 전원측으로 회수되는 무효전력,reactive_power으로
}
이건 송전 관련?
피상전력 = 유효전력 / 역률
cosθ = 역률
유효전력 Pa = V I cosθ = I2 R
무효전력 Pr = V I sinθ = I2 X (X : 리액턴스,reactance)
피상전력 Papp = V I = I2 Z = √(Pa2 + Pr2)
가장 이상적인 경우는 피상전력 = 유효전력인 경우, 즉 역률이 1이 되는 경우.
| AC전력이 여러가지 ... | 기호 | 단위 | |
| 피상전력 apparent power | Papp | V·A | 연결된 부하를 운용하기 위해 발전소에서 보내야 하는 총 전력 |
| 유효전력 active power | Pa | W | 저항에서 소비되는 전력 전기 기기의 소비전력 |
| 무효전력 reactive power | Pr | Var | 부하에서 소비되지 않고 발전소와 부하 사이를 왔다갔다 하는 전력 inductor/capacitor(QQQ 송배전 시스템에 있는?)에 축적되었다가 방출되는 전력 |
피상전력 = 유효전력 / 역률
cosθ = 역률
유효전력 Pa = V I cosθ = I2 R
무효전력 Pr = V I sinθ = I2 X (X : 리액턴스,reactance)
피상전력 Papp = V I = I2 Z = √(Pa2 + Pr2)
가장 이상적인 경우는 피상전력 = 유효전력인 경우, 즉 역률이 1이 되는 경우.
//from https://m.blog.naver.com/jomuljoo5/221201925521 CHK CHK
| 유효전력 | 일을 하는 전력 | V I cosθ |
| 무효전력 | 일을 못하는 전력 | V I sinθ |
| 피상전력 | 전력회사에서 보내는 전력 | V I |
피상전력² = 무효전력² + 유효전력²
6. 전력의 부호 ¶
| 전력이 양(positive) | 에너지 흡수(absorbing energy) |
| 전력이 음(negative) | 에너지 공급(supplying energy) |
| 에너지를 흡수, 전력을 소모/소비 | |
| 에너지를 공급 (ex. 배터리) |
수동소자(R, L, C)의 경우에는 에너지를 내어 놓을 수는 없고 흡수하거나 하지 않을 수 있으므로,
양/음의 부호가 있다.
(전압,voltage에 따른 전류,electric_current의 흐름에 따라)
전류가 높은 전압에서 낮은 전압으로 흐른다:
전류가 높은 전압에서 낮은 전압으로 흐른다:
전력이 소모됨, 부호는 양
전류가 낮은 전압에서 높은 전압으로 흐른다:전력이 공급됨, 부호는 음
소모된 전력(dissipated power, rel 전력손실,power_dissipation)과 공급된 전력(supplied power)의 관계는 서로 부호가 반대인 관계.(소모된 전력) = −(공급된 전력)
전력의 부호 결정하는 법- 전압 공급 방향이 전류와 동일하면 + 부호
- 전압 공급 방향이 전류와 반대면 − 부호
9. 기타 ¶
Watt's law: 장치(device)가 흡수(absorb)하거나 확산(dissipate)하는 power는, 그것에 걸린 전압,voltage과 그것을 통해 흐르는 전류,electric_current의 곱,product이라는 것.
Ohmic power
옴_법칙,Ohm_law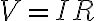 을 전력 식
을 전력 식 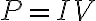 에 적용하면
에 적용하면

이것이 Ohmic_power.
rel. Joule_heating
Joule_heating
 Ohmic power 하면 Joule heating 줄_발열? 처음 결과, 동일 개념.
Ohmic power 하면 Joule heating 줄_발열? 처음 결과, 동일 개념.
rel. Joule_heat 줄 열 ... isa 열,heat
전력공학,power_engineering w
옴_법칙,Ohm_law
rel.
rel. Joule_heat 줄 열 ... isa 열,heat
전력공학,power_engineering w
전력손실,power_dissipation
전력손실,power_dissipation =,power_dissipation 전력손실 power_dissipation
power dissipation
"전력 손실" via power dissipation
power dissipation
// power dissipation ... power dissipation
power dissipation  power dissipation
power dissipation
전력손실,power_dissipation =,power_dissipation 전력손실 power_dissipation
power dissipation
"전력 손실" via
// power dissipation ...


![[http]](/123/imgs/http.png)
![[https]](/123/imgs/https.png)