Difference between r1.42 and the current
@@ -3,42 +3,29 @@
주제:
[[복소수,complex_number]]
[[복소수체,complex_field]] ? - 페이지가 필요?
[[복소평면,complex_plane]]
[[복소함수,complex_function]] - curr goto [[함수,function#s-38]]- [[코시-리만_방정식,Cauchy-Riemann_equation]]
https://samuelj.li/complex-function-plotter/
[[드무아브르_공식,de_Moivre_s_formula]][[오일러_공식,Euler_formula]]
[[일의거듭제곱근,root_of_unity]]
[[일의거듭제곱근,unity_root]]
[[분지,branch]][[주치,principal_value]]
[[함수,function#s-32]](다변수함수 multivariable function)
[[경로적분,contour_integral]]
path_independence, independence_of_the_path
[[미적분학의기본정리,FTC]]와 관련
[[경로,path]] [[경로,contour]] [[독립,independence]]
[[경로,path]] [[경로,contour]] [[독립성,independence]]
[[코시-구르사_정리,Cauchy-Goursat_theorem]][[유수,residue]]
[[극점,pole]] - writing
[[특이점,singular_point]]
{
'''특이점: singular point, singularity'''
'''특이점: singular point, singularity''' // mkl [[특이점,singularity]]
// from wpko
{
@@ -52,12 +39,14 @@
으로 전개할 수 있는데 처음 합을 주부(principal part) 두번째 합을 해석부(analytic part)라 한다. 로랑 급수에서 주부의 항이전혀 나타나지 않으면 제거가능 특이점,
유한개만 나타나면 극점,
무한히 많이 나타나면 본질적 특이점.
무한히 많이 나타나면 본질적 특이점. // Ndict:"본질적 특이점"
}Sub:
[[고립특이점,isolated_singular_point]]
or,
[[고립특이점,isolated_singularity]] WtEn:isolated_singularity ? "isolated singularity" Ndict:"isolated singularity" Ggl:"isolated singularity" Ndict:고립특이점 Ggl:고립특이점
{https://mathworld.wolfram.com/IsolatedSingularity.html
[[WpKo:고립_특이점]]
@@ -155,6 +144,7 @@
= tmp =정칙 holomorphic
n. holomorphy
[[복소함수,complex_function]]가 특정 점 근방에서 미분가능^^differentiable^^(see [[미분가능성,differentiability]])하면 다음 이름이 붙는다고.
holomorphic 정칙(적), 복소해석적
@@ -175,6 +165,9 @@
= tmp links ko =
https://m.blog.naver.com/cindyvelyn/221751578003 - 복소해석학 카테고리 1번글
윤태웅의 복소수함수 강의 - 2022년 2학기 전반부 고려대 전기전자공학부 - YouTube
https://www.youtube.com/playlist?list=PLIzv0-ErbDpyqRVlmnLsGeC_mLmu-dU-L
= books =
Wiki:VisualComplexAnalysis by Wiki:TristanNeedham
@@ -190,8 +183,9 @@
[[Namu:복소해석학]][[Wiki:ComplexAnalysis]]
https://everything2.com/title/complex+analysis
https://artofproblemsolving.com/wiki/index.php/Complex_analysis
----
Up: [[해석학,analysis]]
복소해석학
주제:
복소수,complex_number
복소수체,complex_field ? - 페이지가 필요?
복소평면,complex_plane
복소함수,complex_function - curr goto 함수,function#s-38
드무아브르_공식,de_Moivre_s_formula
오일러_공식,Euler_formula
일의거듭제곱근,unity_root
분지,branch
주치,principal_value
함수,function#s-32(다변수함수 multivariable function)
경로적분,contour_integral
path_independence, independence_of_the_path
코시-구르사_정리,Cauchy-Goursat_theorem
유수,residue
유수정리,residue_theorem
근방,neighborhood
극점,pole - writing
특이점,singular_point
{
특이점: singular point, singularity // mkl 특이점,singularity
복소수,complex_number
복소수체,complex_field ? - 페이지가 필요?
복소평면,complex_plane
복소함수,complex_function - curr goto 함수,function#s-38
드무아브르_공식,de_Moivre_s_formula
오일러_공식,Euler_formula
일의거듭제곱근,unity_root
분지,branch
주치,principal_value
함수,function#s-32(다변수함수 multivariable function)
경로적분,contour_integral
path_independence, independence_of_the_path
코시-구르사_정리,Cauchy-Goursat_theorem
유수,residue
유수정리,residue_theorem
근방,neighborhood
극점,pole - writing
특이점,singular_point
{
특이점: singular point, singularity // mkl 특이점,singularity
// from wpko
{
f가 a를 제외한 f의 한 근방에서 해석적이면 a를 f의 고립특이점(isolated singularity)이라 한다.
고립특이점은 다시 다음으로 구분된다.
점 a가 함수 f의 고립특이점이면, f는 a를 제외한 a 근방에서 로랑_급수,Laurent_series
=\sum_{n=1}^{\infty}\frac{b_n}{(z-a)^n}+\sum_{n=0}^{\infty}a_n(z-a)^n)
으로 전개할 수 있는데 처음 합을 주부(principal part) 두번째 합을 해석부(analytic part)라 한다. 로랑 급수에서 주부의 항이
}
{
f가 a를 제외한 f의 한 근방에서 해석적이면 a를 f의 고립특이점(isolated singularity)이라 한다.
고립특이점은 다시 다음으로 구분된다.
점 a가 함수 f의 고립특이점이면, f는 a를 제외한 a 근방에서 로랑_급수,Laurent_series
}
Sub:
고립특이점,isolated_singular_point
or,
고립특이점,isolated_singularity isolated_singularity ? "isolated singularity"
isolated_singularity ? "isolated singularity"  isolated singularity
isolated singularity  isolated singularity
isolated singularity  고립특이점
고립특이점  고립특이점
고립특이점
{
https://mathworld.wolfram.com/IsolatedSingularity.html
 고립_특이점
고립_특이점
 Isolated_singularity
Isolated_singularity
https://encyclopediaofmath.org/wiki/Isolated_singular_point
https://everything2.com/title/isolated singularity
}
고립특이점,isolated_singular_point
or,
고립특이점,isolated_singularity
{
https://mathworld.wolfram.com/IsolatedSingularity.html
https://encyclopediaofmath.org/wiki/Isolated_singular_point
https://everything2.com/title/isolated singularity
}
removable_singular_point removable_singularity
{
제거가능특이점 없앨수있는특이점
https://mathworld.wolfram.com/RemovableSingularity.html
https://planetmath.org/removablesingularity
 없앨_수_있는_특이점
없앨_수_있는_특이점
 Removable_singularity
Removable_singularity
https://encyclopediaofmath.org/wiki/Removable_singular_point
}
{
제거가능특이점 없앨수있는특이점
https://mathworld.wolfram.com/RemovableSingularity.html
https://planetmath.org/removablesingularity
https://encyclopediaofmath.org/wiki/Removable_singular_point
}
essential_singular_point essential_singularity
{
https://mathworld.wolfram.com/EssentialSingularity.html
https://planetmath.org/essentialsingularity
 본질적_특이점
본질적_특이점
 Essential_singularity
Essential_singularity
https://encyclopediaofmath.org/wiki/Essential_singular_point
https://everything2.com/title/essential singularity
}
{
https://mathworld.wolfram.com/EssentialSingularity.html
https://planetmath.org/essentialsingularity
https://encyclopediaofmath.org/wiki/Essential_singular_point
https://everything2.com/title/essential singularity
}
정칙특이점,regular_singular_point
{
aka regular_singularity ?
푹스 Fuchs Fuchsian equation .... Fuchs_equation ? Fuchsian_equation ? pagename TBD. { https://encyclopediaofmath.org/wiki/Fuchsian_equation }
프로베니우스
{
aka regular_singularity ?
푹스 Fuchs Fuchsian equation .... Fuchs_equation ? Fuchsian_equation ? pagename TBD. { https://encyclopediaofmath.org/wiki/Fuchsian_equation }
프로베니우스
Up: regular_point ? { https://mathworld.wolfram.com/RegularPoint.html }
Opp: irregular_singular_point ? { 설명은 wpen참조. mklink irregular_singularity }
https://mathworld.wolfram.com/RegularSingularPoint.html
 정칙_특이점
정칙_특이점
 Regular_singular_point
Regular_singular_point
https://encyclopediaofmath.org/wiki/Regular_singular_point
https://everything2.com/title/regular singular point
![[http]](/123/imgs/http.png) http://wiki.mathnt.net/index.php?title=정칙특이점(regular_singular_points)
http://wiki.mathnt.net/index.php?title=정칙특이점(regular_singular_points)
}
https://encyclopediaofmath.org/wiki/Regular_singular_point
https://everything2.com/title/regular singular point
![[http]](/123/imgs/http.png) http://wiki.mathnt.net/index.php?title=정칙특이점(regular_singular_points)
http://wiki.mathnt.net/index.php?title=정칙특이점(regular_singular_points)}
Twins:
https://mathworld.wolfram.com/SingularPoint.html
https://mathworld.wolfram.com/Singularity.html
 특이점_(해석학)
특이점_(해석학)
https://encyclopediaofmath.org/wiki/Singular_point
https://everything2.com/title/Singularity
https://mathworld.wolfram.com/SingularPoint.html
https://mathworld.wolfram.com/Singularity.html
https://encyclopediaofmath.org/wiki/Singular_point
https://everything2.com/title/Singularity
1. trig fns와의 관계 ¶
trig functions 관련. ∀z∈ℂ, z=x+iy,
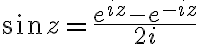 and
and

다음과 같은 친숙한 trig identities는 복소수에서도 똑같이 적용됨
=-\sin z)
=\cos z)
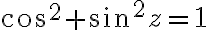
=\sin z_1\cos z_2\pm\cos z_1\sin z_2)
=\cos z_1\cos z_2\mp\sin z_1\sin z_2)
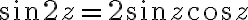
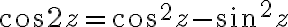
전제는 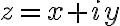 인 듯? CHK
인 듯? CHK
삼각함수, 쌍곡선함수,hyperbolic_function관련해
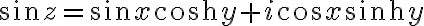

여기에  를 적용하면
를 적용하면
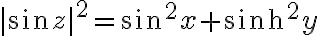
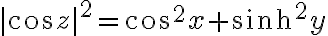
(AEM p846-847)
삼각함수, 쌍곡선함수,hyperbolic_function관련해
sin, cos, sinh, cosh
)
)
)
)

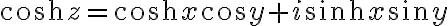
(AEM 848)
2. tmp ¶
정칙 holomorphic
n. holomorphy
n. holomorphy
복소함수,complex_function가 특정 점 근방에서 미분가능differentiable(see 미분가능성,differentiability)하면 다음 이름이 붙는다고.
holomorphic 정칙(적), 복소해석적
holomorphic function 정칙함수 (이상 두개는 kms 번역)
또는 해석적(complex analytic). - 해석함수,analytic_function .... complex_analytic_function?
holomorphic 정칙(적), 복소해석적
holomorphic function 정칙함수 (이상 두개는 kms 번역)
또는 해석적(complex analytic). - 해석함수,analytic_function .... complex_analytic_function?
정칙함수,holomorphic_function or 정칙함수,regular_function - 작성중.
{
/// merge: 해석함수,analytic_function에도 있음
 정칙_함수
정칙_함수
{
/// merge: 해석함수,analytic_function에도 있음
실함수의 미분가능함수+해석함수에 동시에 대응되는 복소함수의 개념이라 함. // 미분가능성,differentiability
}CHK
z = r eiθ means Log z = ln r + iθ.
z = r eiθ means Log z = ln r + iθ.
3. tmp links ko ¶
https://m.blog.naver.com/cindyvelyn/221751578003 - 복소해석학 카테고리 1번글
윤태웅의 복소수함수 강의 - 2022년 2학기 전반부 고려대 전기전자공학부 - YouTube
https://www.youtube.com/playlist?list=PLIzv0-ErbDpyqRVlmnLsGeC_mLmu-dU-L
https://www.youtube.com/playlist?list=PLIzv0-ErbDpyqRVlmnLsGeC_mLmu-dU-L
4. books ¶
https://learning.subwiki.org/wiki/Tristan_Needham
"Visual Complex Analysis (a book that has been praised by many as being good at giving geometric intuition of complex analysis)"
![Amazon:ISBN-0198534469 [ISBN-0198534469]](http://images.amazon.com/images/P/0198534469.01.MZZZZZZZ.gif)
Twins:
https://ghebook.blogspot.com/2012/08/complex-analysis.html
 복소해석학
복소해석학
 Complex_analysis
Complex_analysis
 복소해석학
복소해석학
 ComplexAnalysis
ComplexAnalysis
https://everything2.com/title/complex analysis
https://ghebook.blogspot.com/2012/08/complex-analysis.html
https://everything2.com/title/complex analysis
Up: 해석학,analysis

