복소해석학
주제:
복소수,complex_number
복소수체,complex_field ? - 페이지가 필요?
복소평면,complex_plane
복소함수,complex_function - curr goto 함수,function#s-38
드무아브르_공식,de_Moivre_s_formula
오일러_공식,Euler_formula
일의거듭제곱근,unity_root
분지,branch
주치,principal_value
함수,function#s-32(다변수함수 multivariable function)
경로적분,contour_integral
path_independence - curr. 독립성,independence#s-7
코시-구르사_정리,Cauchy-Goursat_theorem
유수,residue
유수정리,residue_theorem
근방,neighborhood
극점,pole - writing
특이점,singular_point
{
특이점: singular point, singularity // mkl 특이점,singularity
복소수,complex_number
복소수체,complex_field ? - 페이지가 필요?
복소평면,complex_plane
복소함수,complex_function - curr goto 함수,function#s-38
드무아브르_공식,de_Moivre_s_formula
오일러_공식,Euler_formula
일의거듭제곱근,unity_root
분지,branch
주치,principal_value
함수,function#s-32(다변수함수 multivariable function)
경로적분,contour_integral
path_independence - curr. 독립성,independence#s-7
코시-구르사_정리,Cauchy-Goursat_theorem
유수,residue
유수정리,residue_theorem
근방,neighborhood
극점,pole - writing
특이점,singular_point
{
특이점: singular point, singularity // mkl 특이점,singularity
// from wpko
{
f가 a를 제외한 f의 한 근방에서 해석적이면 a를 f의 고립특이점(isolated singularity)이라 한다.
고립특이점은 다시 다음으로 구분된다.
점 a가 함수 f의 고립특이점이면, f는 a를 제외한 a 근방에서 로랑_급수,Laurent_series
=\sum_{n=1}^{\infty}\frac{b_n}{(z-a)^n}+\sum_{n=0}^{\infty}a_n(z-a)^n)
으로 전개할 수 있는데 처음 합을 주부(principal part) 두번째 합을 해석부(analytic part)라 한다. 로랑 급수에서 주부의 항이
}
{
f가 a를 제외한 f의 한 근방에서 해석적이면 a를 f의 고립특이점(isolated singularity)이라 한다.
고립특이점은 다시 다음으로 구분된다.
점 a가 함수 f의 고립특이점이면, f는 a를 제외한 a 근방에서 로랑_급수,Laurent_series
}
Sub:
고립특이점,isolated_singular_point
or,
고립특이점,isolated_singularity isolated_singularity ? "isolated singularity"
isolated_singularity ? "isolated singularity"  isolated singularity
isolated singularity  isolated singularity
isolated singularity  고립특이점
고립특이점  고립특이점
고립특이점
{
https://mathworld.wolfram.com/IsolatedSingularity.html
 고립_특이점
고립_특이점
 Isolated_singularity
Isolated_singularity
https://encyclopediaofmath.org/wiki/Isolated_singular_point
https://everything2.com/title/isolated singularity
}
고립특이점,isolated_singular_point
or,
고립특이점,isolated_singularity
{
https://mathworld.wolfram.com/IsolatedSingularity.html
https://encyclopediaofmath.org/wiki/Isolated_singular_point
https://everything2.com/title/isolated singularity
}
removable_singular_point removable_singularity
{
제거가능특이점 없앨수있는특이점
https://mathworld.wolfram.com/RemovableSingularity.html
https://planetmath.org/removablesingularity
 없앨_수_있는_특이점
없앨_수_있는_특이점
 Removable_singularity
Removable_singularity
https://encyclopediaofmath.org/wiki/Removable_singular_point
}
{
제거가능특이점 없앨수있는특이점
https://mathworld.wolfram.com/RemovableSingularity.html
https://planetmath.org/removablesingularity
https://encyclopediaofmath.org/wiki/Removable_singular_point
}
essential_singular_point essential_singularity
{
https://mathworld.wolfram.com/EssentialSingularity.html
https://planetmath.org/essentialsingularity
 본질적_특이점
본질적_특이점
 Essential_singularity
Essential_singularity
https://encyclopediaofmath.org/wiki/Essential_singular_point
https://everything2.com/title/essential singularity
}
{
https://mathworld.wolfram.com/EssentialSingularity.html
https://planetmath.org/essentialsingularity
https://encyclopediaofmath.org/wiki/Essential_singular_point
https://everything2.com/title/essential singularity
}
정칙특이점,regular_singular_point
{
aka regular_singularity ?
푹스 Fuchs Fuchsian equation .... Fuchs_equation ? Fuchsian_equation ? pagename TBD. { https://encyclopediaofmath.org/wiki/Fuchsian_equation }
프로베니우스
{
aka regular_singularity ?
푹스 Fuchs Fuchsian equation .... Fuchs_equation ? Fuchsian_equation ? pagename TBD. { https://encyclopediaofmath.org/wiki/Fuchsian_equation }
프로베니우스
Up: regular_point ? { https://mathworld.wolfram.com/RegularPoint.html }
Opp: irregular_singular_point ? { 설명은 wpen참조. mklink irregular_singularity }
https://mathworld.wolfram.com/RegularSingularPoint.html
 정칙_특이점
정칙_특이점
 Regular_singular_point
Regular_singular_point
https://encyclopediaofmath.org/wiki/Regular_singular_point
https://everything2.com/title/regular singular point
![[http]](/123/imgs/http.png) http://wiki.mathnt.net/index.php?title=정칙특이점(regular_singular_points)
http://wiki.mathnt.net/index.php?title=정칙특이점(regular_singular_points)
}
https://encyclopediaofmath.org/wiki/Regular_singular_point
https://everything2.com/title/regular singular point
![[http]](/123/imgs/http.png) http://wiki.mathnt.net/index.php?title=정칙특이점(regular_singular_points)
http://wiki.mathnt.net/index.php?title=정칙특이점(regular_singular_points)}
Twins:
https://mathworld.wolfram.com/SingularPoint.html
https://mathworld.wolfram.com/Singularity.html
 특이점_(해석학)
특이점_(해석학)
https://encyclopediaofmath.org/wiki/Singular_point
https://everything2.com/title/Singularity
https://mathworld.wolfram.com/SingularPoint.html
https://mathworld.wolfram.com/Singularity.html
https://encyclopediaofmath.org/wiki/Singular_point
https://everything2.com/title/Singularity
1. trig fns와의 관계 ¶
trig functions 관련. ∀z∈ℂ, z=x+iy,
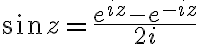 and
and

다음과 같은 친숙한 trig identities는 복소수에서도 똑같이 적용됨
=-\sin z)
=\cos z)
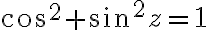
=\sin z_1\cos z_2\pm\cos z_1\sin z_2)
=\cos z_1\cos z_2\mp\sin z_1\sin z_2)
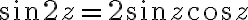
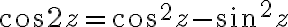
전제는 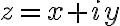 인 듯? CHK
인 듯? CHK
삼각함수, 쌍곡선함수,hyperbolic_function관련해
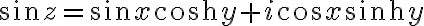

여기에  를 적용하면
를 적용하면
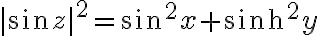
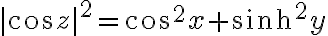
(AEM p846-847)
삼각함수, 쌍곡선함수,hyperbolic_function관련해
sin, cos, sinh, cosh
)
)
)
)

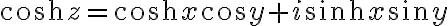
(AEM 848)
2. tmp ¶
정칙 holomorphic
n. holomorphy
n. holomorphy
복소함수,complex_function가 특정 점 근방에서 미분가능differentiable(see 미분가능성,differentiability)하면 다음 이름이 붙는다고.
holomorphic 정칙(적), 복소해석적
holomorphic function 정칙함수 (이상 두개는 kms 번역)
또는 해석적(complex analytic). - 해석함수,analytic_function .... complex_analytic_function?
holomorphic 정칙(적), 복소해석적
holomorphic function 정칙함수 (이상 두개는 kms 번역)
또는 해석적(complex analytic). - 해석함수,analytic_function .... complex_analytic_function?
정칙함수,holomorphic_function or 정칙함수,regular_function - 작성중.
{
/// merge: 해석함수,analytic_function에도 있음
 정칙_함수
정칙_함수
{
/// merge: 해석함수,analytic_function에도 있음
실함수의 미분가능함수+해석함수에 동시에 대응되는 복소함수의 개념이라 함. // 미분가능성,differentiability
}CHK
z = r eiθ means Log z = ln r + iθ.
z = r eiθ means Log z = ln r + iθ.
3. tmp links ko ¶
https://m.blog.naver.com/cindyvelyn/221751578003 - 복소해석학 카테고리 1번글
윤태웅의 복소수함수 강의 - 2022년 2학기 전반부 고려대 전기전자공학부 - YouTube
https://www.youtube.com/playlist?list=PLIzv0-ErbDpyqRVlmnLsGeC_mLmu-dU-L
https://www.youtube.com/playlist?list=PLIzv0-ErbDpyqRVlmnLsGeC_mLmu-dU-L
4. books ¶
https://learning.subwiki.org/wiki/Tristan_Needham
"Visual Complex Analysis (a book that has been praised by many as being good at giving geometric intuition of complex analysis)"
![Amazon:ISBN-0198534469 [ISBN-0198534469]](http://images.amazon.com/images/P/0198534469.01.MZZZZZZZ.gif)
Twins:
https://ghebook.blogspot.com/2012/08/complex-analysis.html
 복소해석학
복소해석학
 Complex_analysis
Complex_analysis
 복소해석학
복소해석학
 ComplexAnalysis
ComplexAnalysis
https://everything2.com/title/complex analysis
https://ghebook.blogspot.com/2012/08/complex-analysis.html
https://everything2.com/title/complex analysis
Up: 해석학,analysis


![Amazon:ISBN-0387985921 [ISBN-0387985921]](http://images.amazon.com/images/P/0387985921.01.MZZZZZZZ.gif)