Difference between r1.25 and the current
@@ -7,7 +7,7 @@
----Given vectors $\vec{v_1},\vec{v_2},\cdots,\vec{v_p}\in\mathbb{R}^n$ and given scalars $c_1,c_2,\cdots,c_p,$ the vector $\vec{y}$ defined by
$\vec{y}=c_1\vec{v_1}+\cdots+c_p\vec{v_p}$
is called a '''linear combination''' of $\vec{v_1},\cdots,\vec{v_p}$ with weights $c_1,\cdots,c_p.$
is called a '''linear combination''' of $\vec{v_1},\cdots,\vec{v_p}$ with [[가중값,weight|weights]] $c_1,\cdots,c_p.$
(Lay)
## from Lay: Linear Combinations
@@ -17,10 +17,11 @@
인 형태를 $\vec{v_1},\vec{v_2},\cdots,\vec{v_k}$ 의 '''일차결합'''(linear combination)이라 한다.## from BigBook LinearAlgebra
----
Let $V$ be a [[벡터공간,vector_space|vector space]] and let $S=\lbrace \vec{v_1},\cdots,\vec{v_k}\rbrace$ be a subset of $V.$
Let $V$ be a [[벡터공간,vector_space|vector space]] and let $S=\lbrace \vec{v_1},\cdots,\vec{v_k}\rbrace$ be a [[부분집합,subset|subset]] of $V.$
A [[벡터,vector|vector]]$a_1\vec{v_1}+\cdots+a_k\vec{v_k}$
for some $a_i\in\mathbb{R}$ is called a '''linear combination''' of $S.$
----
(정의) $x_1,\cdots,x_n$ 의 '''선형결합'''의 형태는
@@ -32,6 +33,7 @@
n-[[튜플,tuple]] $(s_1,s_2,\cdots,s_n)\in\mathbb{R}^n$ 를 변수에 넣어(substitute) 성립하면, 즉$a_1s_1+a_2s_2+\cdots+a_ns_n=d$
이면, [[해,solution]]라고 하거나 '만족한다'고 한다.
----
@@ -54,14 +56,17 @@
여기(선형결합)의 상위개념?// fork later to : [[결합,combination]]?
{
한국어 단어 결합은 저기에서도 쓰임: [[결합,joint]]
이름이 관련
한국어 단어 '결합'의 다른 뜻: 확률론의 [[결합,joint]], 화학의 [[결합,bond]]([[화학결합,chemical_bond]])
같은 영단어 'combination': [[조합,combination]]
// tmp from https://ratsgo.github.io/convex%20optimization/2017/12/25/convexset/ 처음부분
벡터 $x_1,x_2,\cdots,x_n$ 이 있을 때, 이들을 결합하는 방식 세 가지
* [[선형결합,linear_combination]] : $\alpha_1 x_1 + \cdots + \alpha_n x_n \;\; (\alpha_i\in\mathbb{R})$
* [[아핀결합,affine_combination]] : $\alpha_1 x_1 + \cdots + \alpha_n x_n \;\; (\textstyle\sum_i\alpha_i=1)$
* [[볼록결합,convex_combination]] : $\alpha_1 x_1 + \cdots + \alpha_n x_n \;\; (\textstyle\sum_i\alpha_i=1 \,\textrm{ and }\, 0 \le \alpha_i \le 1)$
// tmp 같이 참고: https://blog.naver.com/wjdtjsrms11/222623431037 (중간쯤)
[[아핀결합,affine_combination]]에 대해 닫힌 집합은 [[아핀집합,affine_set]].
[[볼록결합,convex_combination]]에 대해 닫힌 집합은 [[볼록집합,convex_set]].
@@ -78,13 +83,14 @@
[[선형독립,linear_independence]]Twins:
[[WpEn:Linear_combination]]
[[http://terms.naver.com/entry.nhn?docId=3405274&cid=47324&categoryId=47324 수학백과: 일차결합]]
https://mathworld.wolfram.com/LinearCombination.html (easy)
계산 및 출력하는 코드: https://rosettacode.org/wiki/Display_a_linear_combination
Up: [[선형대수,linear_algebra]]
''[[결합,combination]]? [[조합,combination]] 말고''
tmp note: forked from [[여러가지미분표와적분표]]
AKA 일차결합
함수 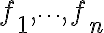
상수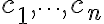 일 때
일 때
linear combination of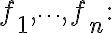
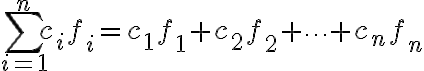
상수
linear combination of
Given vectors 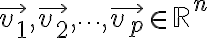 and given scalars
and given scalars 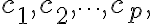 the vector
the vector 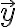 defined by
defined by

is called a linear combination of 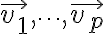 with weights
with weights 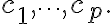
(Lay)
(정의) 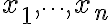 의 선형결합의 형태는
의 선형결합의 형태는
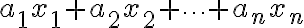
이고 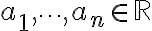 은 결합의 계수,coefficient들이다.
은 결합의 계수,coefficient들이다.
변수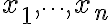 의 선형방정식,linear_equation의 형태는
의 선형방정식,linear_equation의 형태는
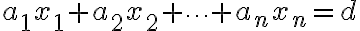
이고 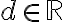 은 상수,constant이다.
은 상수,constant이다.
n-튜플,tuple\in\mathbb{R}^n) 를 변수에 넣어(substitute) 성립하면, 즉
를 변수에 넣어(substitute) 성립하면, 즉
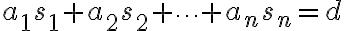
이면, 해,solution라고 하거나 '만족한다'고 한다.
변수
n-튜플,tuple
(Hefferon 1.1 Def)
결합(combination) ¶
여기(선형결합)의 상위개념?
// fork later to : 결합,combination?
{
이름이 관련
한국어 단어 '결합'의 다른 뜻: 확률론의 결합,joint, 화학의 결합,bond(화학결합,chemical_bond)
같은 영단어 'combination': 조합,combination
// fork later to : 결합,combination?
{
이름이 관련
한국어 단어 '결합'의 다른 뜻: 확률론의 결합,joint, 화학의 결합,bond(화학결합,chemical_bond)
같은 영단어 'combination': 조합,combination
// tmp from https://ratsgo.github.io/convex optimization/2017/12/25/convexset/ 처음부분
벡터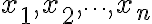 이 있을 때, 이들을 결합하는 방식 세 가지
이 있을 때, 이들을 결합하는 방식 세 가지
// tmp 같이 참고: https://blog.naver.com/wjdtjsrms11/222623431037 (중간쯤)
벡터
// tmp 같이 참고: https://blog.naver.com/wjdtjsrms11/222623431037 (중간쯤)
아핀결합,affine_combination에 대해 닫힌 집합은 아핀집합,affine_set.
볼록결합,convex_combination에 대해 닫힌 집합은 볼록집합,convex_set.
볼록결합,convex_combination에 대해 닫힌 집합은 볼록집합,convex_set.
Twins:
 Linear_combination
Linear_combination
![[http]](/123/imgs/http.png) 수학백과: 일차결합
수학백과: 일차결합
https://mathworld.wolfram.com/LinearCombination.html (easy)
계산 및 출력하는 코드: https://rosettacode.org/wiki/Display_a_linear_combination
![[http]](/123/imgs/http.png) 수학백과: 일차결합
수학백과: 일차결합https://mathworld.wolfram.com/LinearCombination.html (easy)
계산 및 출력하는 코드: https://rosettacode.org/wiki/Display_a_linear_combination
tmp note: forked from 여러가지미분표와적분표


![[https]](/123/imgs/https.png)