열역학,thermodynamics

에너지,energy 및 에너지의 전환, 전달 등에 대해 다루는 학문.
전환, 전달될 때 일,work이나 열,heat의 형태.

열역학적 계 (thermodynamic system)
영어로 에너지 교환 물질 교환
고립계 isolated system × ×
닫힌계 closed system ○ × =밀폐계
열린계 open system ○ ○ =개방계

고립계에서는,
엔트로피,entropy가 증가하는 현상만 일어나며 감소하지 않는다.
ex. 우주 전체

계,system : 관심의 대상이 되는 부분
주위(surroundings): 계를 제외한 나머지 부분
계와 주위를 합쳐 우주(thermodynamic universe).

(논외로, 일반물리 역학부분에서는 계의 에너지를 다룰 때
계(system)
경계(system boundary)
환경(environment)
이렇게 나누는 것을 봤는데... 이런 분류의 차이의 이유는 무엇인지. 아울러,
고립계: 에너지가 계의 경계를 넘을 수 있는 경우 (→ 에너지 보존 법칙 성립)
비고립계: 에너지가 계의 경계를 넘지 않는 경우
이것은 위의 표와도 일치. 즉, '고립'의 주어는 에너지,energy.)

계는 자체의 내부에너지,internal_energy를 갖고 있다.

계와 주위 사이에 벽(wall)이 있는데,
  • diathermal (열을 통과시키는 벽)
  • adiabatic (단열 벽)
이 있다.
경계(boundary)와 같은 말?



[edit]

1. tmp

어떤 계의 전체 에너지 변화 ΔE는 열,heat과 일,work의 합


[edit]

2. Topics

열,heat : 뜨거운 물체에서 차가운 물체로 이동하는 에너지 - 이동하는 만큼의 에너지 자체? 에너지의 흐름을 수치화한 것? 에너지 흐름 '현상'? 에너지 자체일 듯 한데... CHK
온도,temperature T
비열,specific_heat c
열용량,heat_capacity C
엔탈피,enthalpy H
엔트로피,entropy S
내부에너지,internal_energy U
자유에너지,free_energy G

비열 c =비열용량
열용량C
열량 Q =열

비가역반응 irreversible process



[edit]

3. 열역학의 법칙


0 열평형에 대한 서술
1 에너지 보존 법칙
2 엔트로피 증가 법칙
3 절대 0도에 도달할 수 없다는 것

[edit]

3.1. 제 0법칙

A와 B가 열평형(thermal equilibrium)이고,
B와 C가 열평형이면
A와 C도 열평형이다.

이때 B는 온도계(thermometer) 역할을 한다.

다른 말로는,
'온도라는 것이 있다'는 법칙.

[edit]

3.2. 제 1법칙

다른 말로는 에너지보존법칙.
자연계에서 에너지의 총량은 일정하다는 법칙.
우주의 에너지의 양은 변하지 않는다.
에너지는 보존되며 새롭게 만들어지지도 파괴되지도 않는다.
에너지는 창조되지도 파괴되지도 않는다. 우주의 총 에너지는 일정하다. 어떤 계가 에너지를 잃으면 그 주위가 에너지를 얻는다. vice versa.
내부 에너지를 정의한다. (see 내부에너지,internal_energy)

TOCLEANUP
외부와 계 사이에 일,work을 주고받는걸 상상해 본다.
일(W):
시스템이 하는 일 W > 0
시스템이 받는 일 W < 0


--Q--> [ System ] --W-->

그러면 시스템의 에너지의 변화는 +Q-W = 내부에너지의 변화 ΔU = Uf - Ui

ΔU = Uf － Ui = Q － W

복습

Pictorially,
       Heat               Work
        +    +--------+     +
 ----------->| System |----------->
        -    |        |     -
 <-----------|        |<-----------
             +--------+

Sign convention
  • Heat
    • Positive(+) when the system gains
    • Negative(-) when the system loses
  • Work
    • Positive(+) when done by the system
    • Negative(-) when done on the system

Thermal Processes
Type Work 1st Law
Isobaric(P const.) $W=P(V_f-V_i)$ $\Delta U=Q-P(V_f-V_i)$
Isochoric(V const.) $W=0$ $\Delta U=Q-0$
Isothermal(T const.) $W=NkT\ln\left(\frac{V_f}{V_i}\right)$ $0=Q-NkT\ln\left(\frac{V_f}{V_i}\right)$
Adiabatic(Q=0) $W=-\frac32Nk(T_f-T_i)$ $\Delta U=0-W$

ΔE = Q + W (화학)
계가 받은 열(Q)과 계에게 해준 일(W)의 합을 계의 에너지 변화량(ΔE)이라 한다.
여기서 외부 압력에 대해 부피가 변하는 일 외에 다른 일이 없다면,
일은 W = -PΔV, 따라서 ΔE = Q - PΔV

ΔU = Q - W (물리)

[edit]

3.3. 제 2법칙

1법칙은 가능하냐 불가능하냐를 따진다. (possibility) 하지만 제 2법칙은 자발적으로 가능한지를 따진다. (spontaneity)

Clausius의 표현: 열은 자발적으로 낮은온도에서 높은온도로 흐를 수 없다.

Kelvin의 표현: 높은 온도에서 열을 받아서 100% 일로 변환할 수 있는 열기관은 없다.

Boltzmann의 표현: 우주의 엔트로피는 줄어들 수 없다. (같거나 증가한다)

$dS\ge 0$


열기관,heat_engine
{
외연기관 vs 내연기관
}

QC
QH

열기관의 효율
$e=\frac{|W|}{|Q_H|}=\frac{|Q_H|-|Q_C|}{|Q_H|}=1-\frac{|Q_C|}{|Q_H|}$





Carnot
  • 가역반응(reversible process)

carnot engine
carnot refrigerator

[edit]

3.4. 제 3법칙


[edit]

4. 복습

0th law: There exists temperature.
1st law: Energy conservation: ΔU = Q - W
2nd law: Entropy of the universe can not decrease.
3rd law: It is not possible to achieve T = 0 K in a finite number of steps.

[edit]

4.1. merge to 1법칙

[edit]

5. 고딩 교재에서.. TOCLEANUP later

[edit]

5.1. 1법칙

기체에 열(Q)을 가해 외부에 일(W)을 하면, 내부에너지,internal_energy(U)는 (가해 준 열량) - (외부에 한 일의 양)과 같다.
$\Delta U=Q-W=Q-P\Delta V$

tmp from ebs 장인수

$Q=\Delta U+W$
(열) = (내부에너지 변화) + (일)

열 Q의 부호,sign
Q > 0 : 열을 흡수
Q < 0 : 열을 방출
Q = 0 : 단열

내부에너지,internal_energy U의 부호
+ : 증가 = 온도 증가
- : 감소 = 온도 감소
0 : 일정 = 온도 일정
(이건 좀 당연?)

기체가 하는 일
피스톤 단면적 A, 피스톤이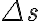 $\Delta s$ 만큼 밀림
$W=F\Delta s=(PA)\Delta s=P\Delta V$

P-V그래프의 밑넓이가 일이라 한다. 따라서 위의 내용
$W=P\Delta V$
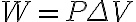
을 일반화하면
$W=\int\nolimits_{V_1}^{V_2}PdV$
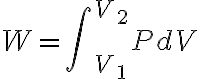
인 것 같다. CHK

일의 부호,sign
압력(P)는 항상 양이라고 한다. (음압같은건 그럼 P<0으로 놓으면 안되고 ΔV < 0??)
W > 0 : W = P ΔV 에서 ΔV > 0 (부피 증가) : 기체가 외부로 일을 했다
W < 0 : W = P ΔV 에서 ΔV < 0 (부피 감소) : 기체가 일을 받았다
W = 0 : ΔV = 0 (부피 일정) : 일을 안했다

정리하면
＋ － 0
Q 열을 흡수 방출 단열
ΔU 증가 감소 일정
W 일을 했다 받았다 안했다

[edit]

5.2. 열역학 과정: 등적변화

=정적과정?
$\Delta V=0$ 이므로, $W=P\Delta V=0$ 이다.

[edit]

5.3. 열역학 과정: 등온변화

온도가 변하지 않았으므로 $\Delta U=0$ 이다.

[edit]

5.4. 열역학 과정: 등압변화

[edit]

5.5. 열역학 과정: 단열변화

단열이란 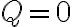$Q=0$

단열팽창
Q=ΔU+W 에서 Q=0, W>0(∵ W=PΔV인데 ΔV>0) 이므로 ΔU<0
즉 온도 감소함.

냉각 방법으로 아주 많이 언급됨. 압축했다가 작은 구멍으로 팽창시키는 것으로.

단열압축
Q=ΔU+W 에서 Q=0, W<0이므로 ΔU>0
즉 온도 증가.

[edit]

6. 열화학,thermochemistry

열역학의 분야. 화학적/물리적 변화에 수반되는 열을 다룸.

발열의 발열성의 exothermic
흡열의 흡열성의 endothermic

endo- : 안으로
exo- : 밖으로


[edit]

7. Links


필기
https://blog.naver.com/hafs_snu/220732342432 1법칙, 각 과정(process)
https://blog.naver.com/hafs_snu/220732342641 2법칙, 카르노, 엔트로피


아주 간단한 열역학 요약
[https]박석재



Related:
통계역학,statistical_mechanics

Misc: 이 학문은 약간 오싹한 느낌이 드는 게, 우주 종말의 한 가능성을 예상할 수 있는 수단이기 때문. (thermodynamic heat death of the universe)