Sub: 유체정역학,fluid_statics
AKA Hydrostatics
Hydrostatics
{
 유체동역학
유체동역학
 Fluid_dynamics
Fluid_dynamics
https://everything2.com/title/fluid dynamics
 Fluid_dynamics
Fluid_dynamics
}
{
AKA 유동
AKA
깊이만큼 압력이 상승하는 식
Sub: 유체동역학,fluid_dynamicsP = P0 + ρgh
{
https://everything2.com/title/fluid dynamics
}
{
AKA 유동
Sub:
선속,flux과 관계 서술
inviscid flow 비점성 유동
irrotational flow 비회전 유동 : 회전,curl을 취했을 때 0이 나오면. / 비회전유동일때만 속도퍼텐셜,velocity_potential을 정의 가능. 속도벡터 u, 속도퍼텐셜 φ 일 때, if ∇×u=0 then u=∇φ. from https://blog.naver.com/mykepzzang/222183327921
비압축성 유동
laminar flow vs turbulent flow : Reynolds number 크기로 구분
층류,laminar_flow { 층류 }
층류 }
난류,turbulent_flow { 난류_(역학) }
난류_(역학) }
tbw:irrotational flow 비회전 유동 : 회전,curl을 취했을 때 0이 나오면. / 비회전유동일때만 속도퍼텐셜,velocity_potential을 정의 가능. 속도벡터 u, 속도퍼텐셜 φ 일 때, if ∇×u=0 then u=∇φ. from https://blog.naver.com/mykepzzang/222183327921
비압축성 유동
laminar flow vs turbulent flow : Reynolds number 크기로 구분
층류,laminar_flow {
난류,turbulent_flow {
선속,flux과 관계 서술
Up: 유체역학,fluid_mechanics > 유체동역학,fluid_dynamics
}
{
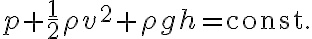
Twins:
 베르누이_방정식
베르누이_방정식
}
와도,vorticity ζ - 회전을 면적으로 나눈것???
베르누이_방정식 베르누이_정리kps물리학용어집 용어에서 vorticity의 번역어로 제시된 것은 '(1) 소용돌이값 (2)소용돌이 벡터'임. via https://www.kps.or.kr/content/voca/search.php?et=en&find_kw=vorticity
![[https]](/123/imgs/https.png) 두산백과: 소용돌이도(vorticity)
두산백과: 소용돌이도(vorticity)
![[https]](/123/imgs/https.png) 기상학백과: 소용돌이도(vorticity)
기상학백과: 소용돌이도(vorticity)
회전,circulation![[https]](/123/imgs/https.png) 두산백과: 소용돌이도(vorticity)
두산백과: 소용돌이도(vorticity)![[https]](/123/imgs/https.png) 기상학백과: 소용돌이도(vorticity)
기상학백과: 소용돌이도(vorticity){
나비에-스톡스_방정식 or 나비에-스토크스_방정식,Navier-Stokes_equation
파스칼의 원리 Pascal's Principle Pascal_principle
{
갇힌 비압축성 유체의 어떤 부분에 압력을 가하면 그 압력이 다른 곳으로 그대로 전달된다.
{
갇힌 비압축성 유체의 어떤 부분에 압력을 가하면 그 압력이 다른 곳으로 그대로 전달된다.
모든 지점에 같은 크기로 전달된다.
유체의 압력은 어느 방향에서나 동일하다.
일부에 가해진 압력은 크기에 관계없이 모든 부분에 골고루 전달된다.
유체의 압력은 어느 방향에서나 동일하다.
일부에 가해진 압력은 크기에 관계없이 모든 부분에 골고루 전달된다.
식으로 나타내면,
우선 압력,pressure의 정의에 의해 압력=힘/면적

인데, 파스칼의 원리는 이를 확장해서
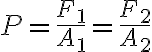
유체가 점성,viscosity이나 압축성,compressibility이 없다는 것이 가정.
우선 압력,pressure의 정의에 의해 압력=힘/면적
아르키메데스의 원리 Archimedes' Principle Archimedes_principle
점도, 점성, viscosity (η, μ)
// from Schaum College Phy p49 {
: 유체에 잠긴 물체는 밀어낸 그 유체의 무게,weight만큼의 부력,buoyant_force을 받는다...는 것 같다.CHK
FB = buoyant force = weight of displaced fluid
어떤 물체에 작용하는 부력은 그 물체에 의해 밀려난 유체의 무게와 같다.
 Archimedes'_principle
Archimedes'_principle
 Archimedes'_principle
Archimedes'_principle
 아르키메데스의_원리
아르키메데스의_원리
부력,buoyant_force: =buoyancy?FB = buoyant force = weight of displaced fluid
어떤 물체에 작용하는 부력은 그 물체에 의해 밀려난 유체의 무게와 같다.
점도, 점성, viscosity (η, μ)
// from Schaum College Phy p49 {
Fluid flow or discharge (J)
단면적 인 파이프에 평균 속력
인 파이프에 평균 속력 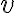 로 유체가 흐르면
로 유체가 흐르면
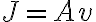
AKA rate of flow, discharge rate
단면적
Equation of continuity // 연속방정식,continuity_equation
incompressible(constant-density) 유체가 파이프로 흐르는데, 한 곳의 단면적은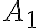 이고 다른 곳의 단면적은
이고 다른 곳의 단면적은 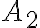 일때, flow는 일정하므로
일때, flow는 일정하므로
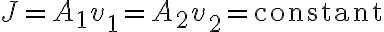
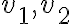 는 각각
는 각각 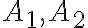 를 지날 때 평균 속력.
를 지날 때 평균 속력.
incompressible(constant-density) 유체가 파이프로 흐르는데, 한 곳의 단면적은
Shear rate
유체가 변할 때의 shear strain. 단위는 s-1.
유체가 변할 때의 shear strain. 단위는 s-1.
점성 Viscosity (η)
a measure of how large a shear stress is required to produce unit shear rate.
일정?(unit) 층밀림비(shear rate)를 만들기 위해 얼마나 큰 층밀림변형력(shear stress)이 필요한지를 측정하는...
단위:
길이 L, 단면반지름 R인 원통형 파이프를 흐르는 fluid flow는
}{8 \eta L})
여기서
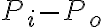 : 파이프 양단의 압력차 (input minus output)
: 파이프 양단의 압력차 (input minus output)
압력이 한 일 Work done by pressure
면적 A인 표면에 압력 P로 눌러서 표면과 수직으로 거리 Δx만큼 눌렀다면,
(그 때문에 부피 변화가 ΔV = A Δx)
압력이 한 일은
a measure of how large a shear stress is required to produce unit shear rate.
일정?(unit) 층밀림비(shear rate)를 만들기 위해 얼마나 큰 층밀림변형력(shear stress)이 필요한지를 측정하는...
단위:
Pa·s or N·s/m2 or kg/m·s - poiseuille (Pl)
poise (P), 1 P = 0.1 Pl
푸아죄유 법칙 Poiseuille's lawpoise (P), 1 P = 0.1 Pl
길이 L, 단면반지름 R인 원통형 파이프를 흐르는 fluid flow는
면적 A인 표면에 압력 P로 눌러서 표면과 수직으로 거리 Δx만큼 눌렀다면,
(그 때문에 부피 변화가 ΔV = A Δx)
압력이 한 일은
Work = P A Δx = P ΔV
(see also 압력,pressure)베르누이방정식 Bernoulli's equation (for the steady flow of a continuous stream of fluid)
흐름경로(stream path)를 따라 두 점이 있다.
점 1은 높이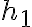 에 있고 그 점에서 속력
에 있고 그 점에서 속력 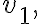 밀도
밀도 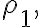 압력
압력 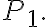
점 2는 높이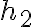 에 있고 그 점에서 속력
에 있고 그 점에서 속력 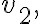 밀도
밀도 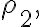 압력
압력 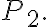
유체가 비압축성이고 점성을 무시하면,
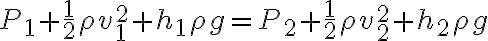
여기서 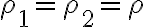 이고
이고 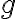 는 중력가속도. (rho를 다 같다고 할거면 위에는 왜 저렇게 구분?)
는 중력가속도. (rho를 다 같다고 할거면 위에는 왜 저렇게 구분?)
흐름경로(stream path)를 따라 두 점이 있다.
점 1은 높이
점 2는 높이
유체가 비압축성이고 점성을 무시하면,
토리첼리 정리 Torricelli's theorem
(참고로 오리피스 orifice = 유체를 분출시키는 구멍)
액체 탱크가 있고 윗부분은 대기압에 노출. 유출구(orifice)가 액체 윗면에서 h만큼 아래에 있다면, speed of outflow from the orifice is
(가정: 액체가 베르누이 방정식을 만족)
(참고로 오리피스 orifice = 유체를 분출시키는 구멍)
액체 탱크가 있고 윗부분은 대기압에 노출. 유출구(orifice)가 액체 윗면에서 h만큼 아래에 있다면, speed of outflow from the orifice is
(가정: 액체가 베르누이 방정식을 만족)
Reynolds number 레이놀즈_수
기호: Re (위키백과), NR (책)
is a dimensionless number that applies to a fluid of viscosity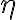 and density
and density 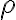 flowing with speed
flowing with speed 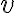 thru a pipe (or past an obstacle) with diameter
thru a pipe (or past an obstacle) with diameter 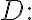
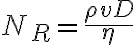
Turbulent flow(난류, 마구흐름) occurs if NR for the flow exceeds about 2000 for pipes or about 10 for obstacles.
기호: Re (위키백과), NR (책)
is a dimensionless number that applies to a fluid of viscosity
// } 이상 Schaum's 유체역학 부분 요약
유체역학 매우 기초 - KU유철상 (tmp) ¶
에너지보존법칙(curr 보존,conservation#s-1)을 방정식 형태로 처음 유도한 사람은 Leonhard_Euler 이다. 그는 뉴턴 제 2법칙을 이용해 다음 미분방정식,differential_equation 형태의 에너지보존법칙을 유도하였다.
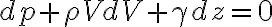
여기서
식의 뜻:
속도에너지는 운동에너지를 뜻하나??
식의 뜻:
(압력 에너지의 변화량) + (속도 에너지의 변화량) + (위치 에너지의 변화량) = 0
(속도 에너지는 속도의 제곱에 비례)속도에너지는 운동에너지를 뜻하나??
fluid_simulation ¶
Understanding Fluid Simulation: Microscopic Perspective
https://www.youtube.com/watch?v=MXs_vkc8hpY
tags: fluid_simulation fluid_dynamics 분자,molecule
But How DO Fluid Simulations Work?
https://www.youtube.com/watch?v=qsYE1wMEMPA
https://www.youtube.com/watch?v=MXs_vkc8hpY
tags: fluid_simulation fluid_dynamics 분자,molecule
But How DO Fluid Simulations Work?
https://www.youtube.com/watch?v=qsYE1wMEMPA
Up: 물리학,physics

