고리 모양 도선에 전류,electric_current가 흐르면 주위에 자기장,magnetic_field이 생긴다.
만약 이 전류가 시간에 따라 변하면, 도선에는 이 변화를 상쇄하는 유도기전력,induced_emf이 생겨서, 처음 흘려준 전류와는 별개의 유도전류,induced_current가 흐르는 데, 이 현상이 자체유도.
만약 이 전류가 시간에 따라 변하면, 도선에는 이 변화를 상쇄하는 유도기전력,induced_emf이 생겨서, 처음 흘려준 전류와는 별개의 유도전류,induced_current가 흐르는 데, 이 현상이 자체유도.
코일에 시간에 따라 변하는 전류가 흐를 때, 코일에 생성된 자기장의 변화가 전자기유도,electromagnetic_induction에 따라 반대방향 기전력,electromotive_force,emf을 유도하는 것.
코일에 흐르는 전류의 세기가 변하면
코일 주위 자기장이 변하며,
이로 인해 코일 자체에 이 자기장의 변화를 방해하는 방향으로(렌츠_법칙,Lenz_s_law)
유도기전력,induced_emf이 발생하여
코일에 유도전류가 흐르는 현상이 ‘자체유도’이다.
코일이 없으면 그런 현상이 없이 바로 전류가 V/R만큼 흐른다.
코일 주위 자기장이 변하며,
이로 인해 코일 자체에 이 자기장의 변화를 방해하는 방향으로(렌츠_법칙,Lenz_s_law)
유도기전력,induced_emf이 발생하여
코일에 유도전류가 흐르는 현상이 ‘자체유도’이다.
코일이 없으면 그런 현상이 없이 바로 전류가 V/R만큼 흐른다.
위 내용을 다시 식으로 표현하면,
(코일에 흐르는) 전류 의 변화
의 변화 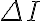 가 시간에 따라 변하면,
가 시간에 따라 변하면,
시간에 대한 전류의 변화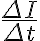 가 유도기전력을 만드는데 ... (생략)
가 유도기전력을 만드는데 ... (생략)

여기서 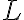 은 자체인덕턴스,self-inductance.
은 자체인덕턴스,self-inductance.
(코일에 흐르는) 전류
시간에 대한 전류의 변화
원형 도선에 전류가 흐르면 자기장이 생긴다. (비오-사바르_법칙,Biot-Savart_law)
코일에 전류가 흐르면 자기장이 코일 속에도 생긴다.
전류가 변하면 코일을 통과하는 자속,magnetic_flux도 변한다. 그리하여 코일에 유도 기전력이 나타난다. 이것이 자체 유도.
코일에 전류가 흐르면 자기장이 코일 속에도 생긴다.
전류가 변하면 코일을 통과하는 자속,magnetic_flux도 변한다. 그리하여 코일에 유도 기전력이 나타난다. 이것이 자체 유도.
이 때 유도기전력의 크기는 전류의 시간에 대한 변화율 ( 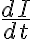 ) 에 비례한다.
) 에 비례한다.
따라서 유도 기전력은,

아울러 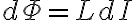 이고,
이고,
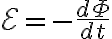
이다.
따라서 유도 기전력은,
가변저항 R과 코일 L이 있는 회로 (RL회로,RL_circuit)에 전류 i가 흐를 때, 가변저항의 접촉점을 옮겨서 코일에 흐르는 전류를 변화시키면 그 동안 자체유도기전력 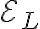 이 생긴다. 이 과정을 자체유도라 하고 이때의 기전력을 자체유도기전력이라고 한다.
이 생긴다. 이 과정을 자체유도라 하고 이때의 기전력을 자체유도기전력이라고 한다.
유도용량 L의 정의에서
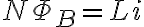
이며, 패러데이_법칙,Faraday_s_law에 의하면
}{dt})
위 두 식을 결합하면
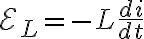 (자체 유도기전력)
(자체 유도기전력)
(유도 기전력은 유도기전력,induced_emf 참조.)
(HRW p. 320)
(HRW p. 320)
코일,coil에 흐르는 전류,electric_current가 변하면 자기장,magnetic_field이 변하고, 이로 인해 코일 자체에 자기장의 변화를 방해하는 방향으로 유도기전력,induced_emf이 발생하는 현상을 자체유도라고 함
전제:
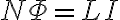
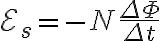
}{\Delta t})
}{\Delta t})
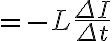
(from SNUON)
유도기에서, 자체유도에 의한 전류의 방향 ¶
코일에는 자기장을 일정하게 유지하려는 (즉, 변화를 감소하려는) 성향이 있다.
좌우로 놓인 코일에서 전류가 오른쪽으로 흐른다고 가정하고,
전류가 증가하면 유도기전력의 방향이 왼쪽이다. (자기장 형성을 방해하려고)
전류가 감소하면 유도기전력의 방향이 오른쪽이다. (자기장 감소를 방해하려고 = 자기장을 유지하려고)

(EBS 장인수)
좌우로 놓인 코일에서 전류가 오른쪽으로 흐른다고 가정하고,
전류가 증가하면 유도기전력의 방향이 왼쪽이다. (자기장 형성을 방해하려고)
전류가 감소하면 유도기전력의 방향이 오른쪽이다. (자기장 감소를 방해하려고 = 자기장을 유지하려고)

(EBS 장인수)


