Difference between r1.64 and the current
@@ -1,44 +1,111 @@
#noindex
Sub:[[접선,tangent_line]]
[[법선,normal_line]]
[[법선벡터,normal_vector]]
[[단위법선벡터,unit_normal_vector]]
[[할선,secant_line]] https://mathworld.wolfram.com/SecantLine.html
https://ko.wikipedia.org/wiki/할선
https://en.wikipedia.org/wiki/Secant_line
[[점근선,asymptote]] - writing
[[준선,directrix]] - w rr
[[무한원선,line_at_infinity]] - writing .... 다른name?
[[중심선,central_line]] - w + w rr
수직parallel
[[직교성,orthogonality]]
trivial: 수평선(horizontal line), 수직선(vertical line), 수직선(number line) -
[[수직선,number_line]], // NN:수직선
사선(oblique line) (=slant? slanted? slanting? incline? isocline?) // NN:사선
(그리고 diagonal과 oblique의 차이는 뭐지? 서술. tbw. - see [[WpEn:Diagonal]] [[WpKo:대각선]])
위 수직선과 아래 실직선의 관계? (내생각,chk) 아마 동의어이거나 실직선에서 필요에 따라 정수만 표기하거나 한게(부분집합 비슷한 게) 수직선? 수직선에서 수가 실수임을 명시한 게 실직선?
→ 일단 real line의 고정된 정의가 없음(MW), 대충 usage 차이/disambiguation서술 정도로 족할 듯.
[[점근선,asymptote]] - writing
[[준선,directrix]]
https://everything2.com/title/Directrix (tmp)
실직선 real line / real number line ... Ggl:"real number line" ...aka 실수직선?
KmsE:실직선 { "real line 실직선" }
([[기하학,geometry]]의 '''직선'''과 [[해석학,analysis]]의 [[실수,real_number]]는 누구나 느낄 수 있는 '밀접한 관계'가 있는데 정확히 전문적으로? tbw, 아마 real line이 그 중간쯤의 영역에 있는 표현?)
https://mathworld.wolfram.com/RealLine.html
''"has a number of different meanings" 즉 완벽히 고정된 정의는 없음.''
Sub:
// [[확장,extension]] of real number ? ... { cf. extended_natural_number { WpEn:Extended_natural_numbers } }
// KmsE:extended
extended_real_xxx
{
extended real number line
extended real line
extended real number system
WpEn:Extended_real_number_line
REL
extended_real_number
{
'''extended real number'''
WpJa:拡大実数
Sub:
affinely_extended_real_number
{
'''affinely extended real number'''
}// affinely extended real number ... Ggl:"affinely extended real number"
}// extended real number ... Ggl:"extended real number"
cf. [[리만_구,Riemann_sphere]] ([[복소수,complex_number]]의 경우)
Sub:
projectively_extended_real_line
{
'''projectively extended real line'''
여기선 $+\infty,-\infty$ 를 $\infty$ 하나로 합쳤다
WpEn:Projectively_extended_real_line
}//projectively extended real line ... Ggl:"projectively extended real line"
}// extended real line ... Ggl:"extended real line"
Sorgenfrey_line - [[반례,counterexample]]로 자주 쓰이는 // MKL [[standard_topology]] 표준위상 ? WtEn:standard_topology ... rel [[nonstandard_topology]](?? Ggl:비표준위상 ?)
Sorgenfrey line
https://mathworld.wolfram.com/SorgenfreyLine.html x 2024-01
https://planetmath.org/sorgenfreyline
AKA lower limit topology = lower_limit_topology =,lower_limit_topology . "lower limit topology" Ggl:"lower limit topology"
"The '''Sorgenfrey line''' is first countable and separable, but is not second countable. It is therefore not metrizable." // MKL [[위상,topology]] [[countability]] [[metrizability]]
https://proofwiki.org/wiki/Definition:Sorgenfrey_Line
https://topospaces.subwiki.org/wiki/Sorgenfrey_line
Ggl:"Sorgenfrey line"
Ndict:"Sorgenfrey line" x 2023-12
Naver:"Sorgenfrey line"
rel. Sorgenfrey_plane - 역시 [[반례,counterexample]]로 자주 쓰이는
Sorgenfrey plane
WpEn:Sorgenfrey_plane
https://topospaces.subwiki.org/wiki/Sorgenfrey_plane
"Sorgenfrey plane"
Ggl:"Sorgenfrey plane"
KmsE:Sorgenfrey x 2023-12
Up: [[위상수학,topology]]
long_line
long line
[[WpKo:긴_직선]] = https://ko.wikipedia.org/wiki/긴_직선
[[WpEn:Long_line_(topology)]]
"long line (or Alexandroff line)"
https://ncatlab.org/nlab/show/long+line
Up: [[위상수학,topology]]
Compare:
'''직선(straight line)''' vs [[곡선,curve]] - [[방향,direction]]이 일정한 지 여부
'''직선'''은 [[곡률,curvature]]이 0인 곡선임.
[[선분,line_segment]]
{
두 개의 끝점 ([[점,point]])으로.. 정의?
[[직선,line]]의 [[부분,part]] or [[부분집합,subset]]?
[[MathWorld:LineSegment]]
= https://mathworld.wolfram.com/LineSegment.html
[[WpKo:선분]]
= https://ko.wikipedia.org/wiki/선분
[[WpEn:Line_segment]]
= https://en.wikipedia.org/wiki/Line_segment
[[다포체,polytope]]위키에선 dyad라고도? https://polytope.miraheze.org/wiki/Dyad
}
[[반직선,ray]]{
WpKo:반직선
= https://ko.wikipedia.org/wiki/반직선
}
[[축,axis]]서로 다른 '''직선'''이 [[점,point]]에서 만나면 [[각,angle]]이 생김
@@ -49,6 +116,65 @@
[[방향,direction]]이 있고, 일정하다. 그러나 [[벡터,vector]]와는 달리 [[위치,position]]가......TBW<<TableOfContents>>
= 2D 평면에서 =
([[평면,plane]] 위의 직선)
한 점 $P_0(x_0,y_0)$ 를 지나고 [[기울기,slope]]가 $m$ 인 '''직선'''의 방정식은
$\frac{y-y_0}{x-x_0}=m$
즉
$y-y_0=m(x-x_0)$
$y=m(x-x_0)+y_0$
으로 구할 수 있다.
= 3D 공간에서 =
from https://youtu.be/e9L17SoGT8c?t=3649
Vector equation of a '''line''':
$\vec{r} (t) = \vec{r_0} + t\vec{v}$
$\langle x(t),y(t),z(t) \rangle$
$= \langle x_0,y_0,z_0 \rangle + t \langle a,b,c \rangle$
$= \langle x_0,y_0,z_0 \rangle + \langle at,bt,ct \rangle$
$= \langle x_0+at,y_0+bt,z_0+ct \rangle$
Parametric equations of a '''line''':
$x(t)=x_0 + at$
$y(t)=y_0 + bt$
$z(t)=z_0 + ct$
이 두 방정식은 점 $(x_0,y_0,z_0 )$ 을 지나며 [[방향벡터,direction_vector]] $\vec{v}=\langle a,b,c\rangle$ 방향의 '''직선'''을 표현.
----
([[공간,space]] esp. 3D [[유클리드_공간,Euclidean_space]] 안의 직선)
직선과 평행한 [[벡터,vector]]를 $\vec{v}=(a,b,c)$ 라 하고
직선 위의 한 점 $P_0(x_0,y_0,z_0)$ 를 지나고 벡터 $\vec{v}$ 와 평행한 직선 위의 임의의 점을 $P(x,y,z)$ 라 하면
벡터 $\vec{P_0P}$ 는 $\vec{v}$ 와 평행([[평행성,parallelism]])하므로
$\vec{P_0P}=t\vec{v}$ ... (1)
인 실수 $t$ 가 존재한다.
$\vec{OP}=\vec{r},\;\vec{OP_0}=\vec{r_0}$
이라고 하면 (1)을 다음과 같이 쓸 수 있다.
$\vec{r}-\vec{r_0}=t\vec{v}$
$\vec{r}=\vec{r_0}+t\vec{v}$
이 식을 직선의 [[벡터방정식,vector_equation]]이라고 한다.
또한 (1)을 성분별로 나타내면
$(x-x_0,y-y_0,z-z_0)=(ta,tb,tc)$
이므로 다음과 같이 쓸 수 있다.
$x=x_0+at,$
$y=y_0+bt,$
$z=z_0+ct\;\;\;(-\infty<t<\infty)$
이 식을 직선의 [[매개변수방정식,parametric_equation]]이라고 한다.
또한 매개변수방정식에서 매개변수 $t$ 를 소거하여
$\frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}\;\;\;(abc\ne 0)$
로 나타낸 것을 직선의 [[대칭방정식,symmetric_equation]]이라고 한다.
만약 $a,b,c$ 중에서 0이 있어도 매개방정식에서 매개변수를 소거하는 것이 가능하다.
예를 들어 $a=0$ 이라면
$x=x_0,\,\frac{y-y_0}{b}=\frac{z-z_0}{c}$
로 나타낼 수 있다. 이때 직선은 x축과 수직인 평면 $x=x_0$ 에 포함된다. [* 서울대기초수학학습교재 p23]
= tmp CLEANUP =
{
@@ -139,13 +265,19 @@
$d$ 는 원점에서 직선까지의 (최단)거리. $\beta$ 는 원점에서 직선까지 거리를 표시하는 선의 각.(Heinbockel Vol1 p39)
= 직선에 대한 표현 =
= 직선에 대한 표현 ... 이라기보단 두 직선의 위치관계? =
== skew lines ==from wpsimple: 평행parallel하지도 교차intersecting하지도 않음. 같은 [[평면,plane]]에 있을 수 없음. 3차원(이상?)에서만 존재 가능.
[[WpSimple:Skew_lines]]
[[WpEn:Skew_lines]]
[[WpKo:꼬인_위치]]
https://mathworld.wolfram.com/SkewLines.html
----
꼬인 직선
평면에서 평행하지 않은 두 직선은 한 점에서 만난다. 그러나 공간에서 두 직선은 평행하지 않아도 만나지 않는 경우가 있다. 이런 경우 두 직선은 '''꼬인 위치에 있다'''고 한다. [* 서울대기초수학학습교재 p25]
[[평행,parallel]] .... [[평행성,parallelism]](writing)
@@ -181,7 +313,16 @@
[[방정식,equation]]https://everything2.com/title/vector+equation+of+a+line
https://everything2.com/title/Symmetric+equation+of+a+line
= QQQ CHK =
'''직선'''의 각 [[점,point]]들과 [[실수,real_number]]들을 [[일대일대응,one-to-one_correspondence]] 가능?
직선 위의 점 P ⇔ 실수 x
평면 위의 점 P ⇔ 실수의 쌍 (x, y)
(수학의 정석)
https://mathworld.wolfram.com/Line.html
Up: [[기하학,geometry]]
Sub:
{
두 개의 끝점 (점,point)으로.. 정의?
직선,line의 부분,part or 부분집합,subset?
접선,tangent_line
법선,normal_line
할선,secant_line https://mathworld.wolfram.com/SecantLine.html
점근선,asymptote - writing
준선,directrix - w rr
무한원선,line_at_infinity - writing .... 다른name?
중심선,central_line - w + w rr
trivial: 수평선(horizontal line), 수직선(vertical line), 수직선(number line) -
 real number line ...aka 실수직선?
real number line ...aka 실수직선?
 실직선 { "real line 실직선" }
실직선 { "real line 실직선" }
(기하학,geometry의 직선과 해석학,analysis의 실수,real_number는 누구나 느낄 수 있는 '밀접한 관계'가 있는데 정확히 전문적으로? tbw, 아마 real line이 그 중간쯤의 영역에 있는 표현?)
https://mathworld.wolfram.com/RealLine.html
// 확장,extension of real number ? ... { cf. extended_natural_number { Extended_natural_numbers } }
Extended_natural_numbers } }
// extended
extended
extended_real_xxx
Sorgenfrey_line - 반례,counterexample로 자주 쓰이는 // MKL standard_topology 표준위상 ?  standard_topology ... rel nonstandard_topology(??
standard_topology ... rel nonstandard_topology(??  비표준위상 ?)
비표준위상 ?)
 Sorgenfrey x 2023-12
Sorgenfrey x 2023-12
Up: 위상수학,topology
long_line
Compare:법선,normal_line
할선,secant_line https://mathworld.wolfram.com/SecantLine.html
점근선,asymptote - writing
준선,directrix - w rr
무한원선,line_at_infinity - writing .... 다른name?
중심선,central_line - w + w rr
trivial: 수평선(horizontal line), 수직선(vertical line), 수직선(number line) -
수직선,number_line, //  수직선
수직선
사선(oblique line) (=slant? slanted? slanting? incline? isocline?) // 사선
사선
(그리고 diagonal과 oblique의 차이는 뭐지? 서술. tbw. - see Diagonal
Diagonal  대각선)
대각선)
위 수직선과 아래 실직선의 관계? (내생각,chk) 아마 동의어이거나 실직선에서 필요에 따라 정수만 표기하거나 한게(부분집합 비슷한 게) 수직선? 수직선에서 수가 실수임을 명시한 게 실직선?사선(oblique line) (=slant? slanted? slanting? incline? isocline?) //
(그리고 diagonal과 oblique의 차이는 뭐지? 서술. tbw. - see
→ 일단 real line의 고정된 정의가 없음(MW), 대충 usage 차이/disambiguation서술 정도로 족할 듯.
실직선 real line / real number line ... (기하학,geometry의 직선과 해석학,analysis의 실수,real_number는 누구나 느낄 수 있는 '밀접한 관계'가 있는데 정확히 전문적으로? tbw, 아마 real line이 그 중간쯤의 영역에 있는 표현?)
https://mathworld.wolfram.com/RealLine.html
"has a number of different meanings" 즉 완벽히 고정된 정의는 없음.
Sub:// 확장,extension of real number ? ... { cf. extended_natural_number {
//
extended_real_xxx
{
extended real number line
extended real line
extended real number system
 Extended_real_number_line
Extended_real_number_line
REL
extended_real_number
Sub:
projectively_extended_real_line
 extended real line
extended real line
extended real number line
extended real line
extended real number system
REL
extended_real_number
{
extended real number
 拡大実数
拡大実数
Sub:
affinely_extended_real_number
}// extended real number ... extended real number
extended real number
cf. 리만_구,Riemann_sphere (복소수,complex_number의 경우) extended real number
Sub:
affinely_extended_real_number
}// extended real number ...
Sub:
projectively_extended_real_line
{
projectively extended real line
여기선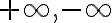 를
를 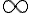 하나로 합쳤다
하나로 합쳤다
 Projectively_extended_real_line
Projectively_extended_real_line
}//projectively extended real line ... projectively extended real line
projectively extended real line
}// extended real line ... projectively extended real line
여기선
}//projectively extended real line ...
Sorgenfrey line
https://mathworld.wolfram.com/SorgenfreyLine.html x 2024-01
https://planetmath.org/sorgenfreyline
https://topospaces.subwiki.org/wiki/Sorgenfrey_line
 Sorgenfrey line
Sorgenfrey line
 Sorgenfrey line x 2023-12
Sorgenfrey line x 2023-12
 Sorgenfrey line
Sorgenfrey line
rel. Sorgenfrey_plane - 역시 반례,counterexample로 자주 쓰이는
https://mathworld.wolfram.com/SorgenfreyLine.html x 2024-01
https://planetmath.org/sorgenfreyline
AKA lower limit topology = lower_limit_topology =,lower_limit_topology . "lower limit topology"  lower limit topology
lower limit topology
"The Sorgenfrey line is first countable and separable, but is not second countable. It is therefore not metrizable." // MKL 위상,topology countability metrizability
https://proofwiki.org/wiki/Definition:Sorgenfrey_Line"The Sorgenfrey line is first countable and separable, but is not second countable. It is therefore not metrizable." // MKL 위상,topology countability metrizability
https://topospaces.subwiki.org/wiki/Sorgenfrey_line
rel. Sorgenfrey_plane - 역시 반례,counterexample로 자주 쓰이는
Sorgenfrey plane
 Sorgenfrey_plane
Sorgenfrey_plane
https://topospaces.subwiki.org/wiki/Sorgenfrey_plane
"Sorgenfrey plane"
 Sorgenfrey plane
Sorgenfrey plane
https://topospaces.subwiki.org/wiki/Sorgenfrey_plane
"Sorgenfrey plane"
Up: 위상수학,topology
long_line
long line
 긴_직선 = https://ko.wikipedia.org/wiki/긴_직선
긴_직선 = https://ko.wikipedia.org/wiki/긴_직선
 Long_line_(topology)
Long_line_(topology)
Up: 위상수학,topology"long line (or Alexandroff line)"
https://ncatlab.org/nlab/show/long line{
두 개의 끝점 (점,point)으로.. 정의?
직선,line의 부분,part or 부분집합,subset?
= https://mathworld.wolfram.com/LineSegment.html
= https://ko.wikipedia.org/wiki/선분
= https://en.wikipedia.org/wiki/Line_segment
다포체,polytope위키에선 dyad라고도? https://polytope.miraheze.org/wiki/Dyad
}
{
}
서로 다른 직선이 점,point에서 만나면 각,angle이 생김
직선의 기울기,slope를 생각 가능.
직선-직선간, 직선-점 간, 직선-평면간, (또 있으면 여기 추가) 등의 거리,distance를 생각 가능.
2. 3D 공간에서 ¶
Vector equation of a line:
 = \vec{r_0} + t\vec{v})
,y(t),z(t) \rangle)



Parametric equations of a line:
=x_0 + at)
=y_0 + bt)
=z_0 + ct)
이 두 방정식은 점 ) 을 지나며 방향벡터,direction_vector
을 지나며 방향벡터,direction_vector 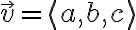 방향의 직선을 표현.
방향의 직선을 표현.
직선과 평행한 벡터,vector를 ) 라 하고
라 하고
직선 위의 한 점) 를 지나고 벡터
를 지나고 벡터  와 평행한 직선 위의 임의의 점을
와 평행한 직선 위의 임의의 점을 ) 라 하면
라 하면
벡터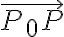 는
는  와 평행(평행성,parallelism)하므로
와 평행(평행성,parallelism)하므로
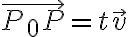 ... (1)
... (1)
인 실수 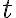 가 존재한다.
가 존재한다.

이라고 하면 (1)을 다음과 같이 쓸 수 있다.
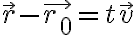
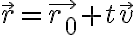
이 식을 직선의 벡터방정식,vector_equation이라고 한다.
직선 위의 한 점
벡터
3. tmp CLEANUP ¶
{
ex.
3차원 공간에서 직선의 방정식
i.e. from http://www.kocw.net/home/search/kemView.do?kemId=1141060 6.
{
직선 위 임의의 점을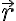 이라 하면,
이라 하면,
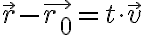
따라서
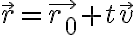
)
)
)
ex.
3차원 공간에서 직선의 방정식
i.e. from http://www.kocw.net/home/search/kemView.do?kemId=1141060 6.
{
직선 위 임의의 점을
그러면
위 식에서 매개변수를 소거하면
(여기선 헷갈리므로 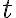 대신
대신 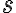 를 쓰면)
를 쓰면)
\quad (s\le 0))
\vec{r_1}\quad (s\le 0))
선분 \vec{r_0} + t\vec{r_1}\quad (0 \le t \le 1))
(rel. 내분 internal division, 내분점 internally dividing point (kms) ... 내분,internal_division, 내분점,internally_dividing_point)
}
}
두 점 ,\,Q=(x_2,y_2,z_2)) 이 주어졌으면
이 주어졌으면
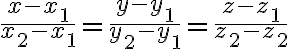
t,\;y=y_1+(y_2-y_1)t,\;z=z_1+(z_2-z_1)t)
)
2차원에서는주어진 직선과 평행한 벡터인 방향벡터,direction_vector를 생각 가능. see 방향수,direction_number, later 방향,direction.
}
직선은 일차방정식(선형방정식,linear_equation)의 해 또는 그래프와 관련.
6. 직선의 polar form ¶
straight line의 극형식,polar_form은 밑의 intercept form에서 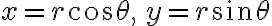 를 넣어서
를 넣어서
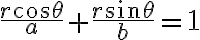
이건 간단히 하면 다음 꼴이 됨 (과정 생략, 그림 필요하고 복잡. 책 참조.)
=d)
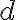 는 원점에서 직선까지의 (최단)거리.
는 원점에서 직선까지의 (최단)거리. 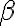 는 원점에서 직선까지 거리를 표시하는 선의 각.
는 원점에서 직선까지 거리를 표시하는 선의 각.
(Heinbockel Vol1 p39)
(Heinbockel Vol1 p39)
7.1. skew lines ¶
from wpsimple: 평행parallel하지도 교차intersecting하지도 않음. 같은 평면,plane에 있을 수 없음. 3차원(이상?)에서만 존재 가능.
 Skew_lines
Skew_lines
 Skew_lines
Skew_lines
 꼬인_위치
꼬인_위치
https://mathworld.wolfram.com/SkewLines.html
https://mathworld.wolfram.com/SkewLines.html
꼬인 직선
평면에서 평행하지 않은 두 직선은 한 점에서 만난다. 그러나 공간에서 두 직선은 평행하지 않아도 만나지 않는 경우가 있다. 이런 경우 두 직선은 꼬인 위치에 있다고 한다. [2]
8. Misc: 2D 직선 방정식 여러 꼴의 영어 표현 ¶
고정점 ) 을 지나고 기울기가
을 지나고 기울기가 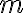 인 직선의 방정식은
인 직선의 방정식은
) (point-slope form of the equation of a line)
(point-slope form of the equation of a line)
y절편이 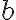 이면 점
이면 점 ) 를 지나므로 위에 대입하면
를 지나므로 위에 대입하면 ) 따라서
따라서
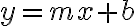 (slope-intercept form)
(slope-intercept form)
수직선(vertical line)등을 포함한 일반적인 꼴은
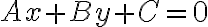 (A and B not both 0) (general linear equation)
(A and B not both 0) (general linear equation)
(Varberg)
point-slope equation of the line
)
slope-intercept equation of the line
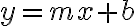
general linear equation (A and B not both 0)
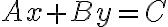
(Thomas)
general equation
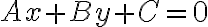
slope-intercept form
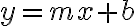
intercept form - y축을 (0,b)에서, x축을 (a,0)에서 만날 경우 (절편)
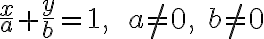
(Heinbockel Vol 1 p38)

