체,field

체 (field)

대충 사칙연산=가감승제(기본적 산술,arithmetic 연산,operation 네가지, 단 division_by_zero만 제외?)를 자유롭게 할 수 있는 수들의 집합? 또는 거기에 연산도 포함? - 수들의 집합인듯.
2023-06-13
- 글쎄? 단순 집합 같지 않은데? 실수체가 다루는 수의 집합을 실수라고도 하고, 실수체를 실수라고도 하고, 이런 용어 사용 같은데?
- 추상대수,abstract_algebra에서 다루는 구조,structure 중 하나?

'가감승제가 자유로운 집합'. 유리수체(유리수 전체의 집합), 실수체, etc. 실수체 = 실수 전체의 집합. (김홍종)
사칙계산에 대해 닫혀 있는 집합을 체(field)라 부른다. (박부성)

ex.
복소수(집합)는 체.
자연수, 정수는 체 아님. (나눗셈,division이 자유롭지 않음)

집합,set F가 다음 성질을 갖는다면, F는 체.
chk, tmp from https://youtu.be/sDZB7ozFytk?t=297 - 강의교재는 Friedberg lin alg.
  • 두 이항연산,binary_operation을 가짐 - (+, ·)
  • 닫힘(closed)
  • 덧셈 교환법칙 a+b=b+a
  • 곱셈 교환법칙 a·b=b·a
  • 덧셈 결합법칙 (a+b)+c=a+(b+c)
  • 곱셈 결합법칙 (a·b)·c=a·(b·c)
  • 덧셈 항등원 존재 0+a=a+0=a ...영,zero?
  • 곱셈 항등원 존재 1·a=a·1=a ...하나,one?
  • 덧셈 역원 존재 ∃-a st a+(-a)=0
  • 곱셈 역원 존재 ∃b-1 st b·b-1=1
  • 덧셈과 곱셈 분배법칙 a·(b+c)=a·b+a·c


참고로 용어
0 : additive identity
1 : multiplicative identity
r에 대해 -r: additive inverse
0을 제외한 r에 대해 r-1: multiplicative inverse
// 항등원,identity_element and 역원,inverse_element

순서체,ordered_field(writing)와 순서체가 아닌 체가 있음

체는 수 없이 많은데..
스칼라체,scalar_field
유한체,finite_field (= Galois field)
{
AKA 유한체 finite field, 갈루아 체 Galois field
유한체를 GF()로 쓰는 것이 이 때문? chk

원소의 개수가 유한 개인 체,field.

ex. 정수를 어떤 소수,prime_number $p$ 로 나눈 나머지,remainder만으로 만든 집합,set
$\mathbb{Z}_p = \lbrace 0, 1, \cdots, p-1 \rbrace$
에 나머지 덧셈과 나머지 곱셈을 연산으로 준 것

See examples(보기): [https]수학백과: 체

rel.
유한체 and 확대체,extension_field => 유한확대체 (curr at 확대체)? chk
이건 AES에 쓰임.



Up: 체,field
}
확대체,extension_field - 작성중
부분체,subfield - 작성중
분수체,fraction_field
{
분수체, field of fractions, fraction field, field of quotients, quotient field

정역,integral_domain에 대해 정의? chk

이름에 분수,fraction 몫,quotient 있는데 mklink



[https]수학백과: 분수체
"주어진 정역을 포함하는 최소의 체(field)를 뜻하며 몫체(field of quotients)라고 하기도 한다."
}
완비체,complete_field - writing
수체,number_field
{
수체 number field
//tmp from https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=number field
{
algebraic number field 대수적 수체
rational number field 유리수체
real number field 실수체
complex number field 복소수체
}
https://ncatlab.org/nlab/show/number field
}
소체,prime_field - writing
분해체,splitting_field - writing
...
준동형사상,homomorphism이란 두 체 사이에서 구조를 보존하는 사상,map인데 정작 체에서는 준동형사상 개념을 잘 안 쓴다고 서술.. (수학백과 참조)
표수 - 환,ring#s-6참조.



[edit]

1. 체인 것의 예 


 + 0 1      · 0 1
 0 0 1      0 0 0
 1 1 0      1 0 1
// 위 행렬이 대칭행렬,symmetric_matrix ↔ 교환법칙,commutativity 성립이다. - chk
[edit]

2. 체가 아닌 것의 예

  • 그런데 $Z_4$ 는 field가 아니다. ∴ There is no multiplicative_inverse of 2 in Z4 (multiplicative_inverse of 2 가 Z4안에 없음):
    2·0=0
    2·1=2
    2·2=0
    2·3=2 ... 를 보면 2에 무엇을 곱하더라도 절대 1이 나오지 않는다 - 숫자 2에 대한 곱셈의 역원이 존재하지 않는다
  • 자연수,natural_number ℕ // ex. 3의 곱셈의 역원이 없다
  • 정수,integer ℤ

(Src: [https]Young Gil Kim)


[edit]

3. Borel field

보렐 집합체 Borel_field
결과,outcome들의 집합인 표본공간,sample_space을 entire real line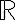 $\mathbb{R}$ 로 잡기에 너무 큰 경우, all events of practical interest를 포함한 더 작은 class를 잡는다. 이것을 Borel field 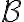$\mathcal{B}$ 이라 한다.

related?: event_class (goto 사건,event#s-9)
(Leon-Garcia 2.2.2 Continuous Sample Spaces; p37; Section 2.9 discusses B in more detail.)



chk: borel sigma field 와 borel field 의 정확한 관계?
보렐 시그마-체(Borel sigma field), Borel sigma-algebra
https://seoncheolpark.github.io/book/_book/4-5-borel-sigma-field.html

[edit]

4. skew field

skew_field = division_ring = 나눗셈대수,division_algebra
(kms: skew field = 꼬인 체 = 비가환체 = 나눗셈환,division_ring... pagename TBD)
see 환,ring, https://mathworld.wolfram.com/DivisionAlgebra.html


곱셈의 가환 조건을 만족하지 않으면 꼬인 체 ? chk

[edit]

5. See also

[edit]

6. 추가


정의:
체,field $F$ 가
단항연산,unary_operation
$':F\to F,$
$(a+b)'=a'+b',$
$(ab)'=a'b+ab'$
을 가지고 있을 때, 체 $F$ 를 미분체(differential field)라 부른다.

예: 유리식,rational_expression의 집합 $\mathbb{C}(x)$

이후 글에서
대수적확대체
로그확대체
지수함수확대체 ..등등 설명.

WtEn:differential_field
"differential field"
Ggl:differential field
}