장,field

AKA: 마당, 場
공간 내의 위치를 독립변수로 갖는 함수
독립변수가 공간의 위치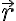 $\vec{r}$ 인 경우의 함수
어떤 영역 내의 모든 곳에서 특정한 양을 규정하는 함수
(공간,space 유클리드_공간,Euclidean_space 독립변수,independent_variable 위치,position 위치벡터,position_vector 함수,function)
spatial distribution of a quantity

스칼라,scalar장과 벡터,vector장이 있음
각각 (값이 스칼라), (값이 벡터)

일반적으로/수학적으로 정의역,domain이 공간,space인 함수,function? 치역은 스칼라,scalar(의 집합), 벡터,vector(의 집합) 외 다른 게 있는지?

스칼라장,scalar_field의 예
건물 내 온도 분포
극장 내 소리의 세기
어떤 공간 영역 내의 전위,electric_potential분포
층을 이룬 매질의 굴절률,refractive_index 분포
벡터장,vector_field의 예
전기장,electric_field
자기장,magnetic_field
공간 내의 물체에 작용하는 중력
대기 중 빗방울의 속도
(Examples from Sadiku 전자기학 5e)

스칼라장의 예
압력장 pressure field p(x,y,z,t) - 압력,pressure
온도장 temperature field T(x,y,z,t) - 온도,temperature
밀도장 density field ρ(x,y,z,t) - 밀도,density
벡터장의 예
속도장 velocity field v(x,y,z,t) - 속도,velocity - 특히 유체역학,fluid_mechanics
전자기장,electromagnetic_field
중력장,gravitational_field

기타 field의 분류
  • static field (time-invariant field)
  • time-varying field 시간에 대해 변하는 장, 시변장
or[1]
  • time-dependent field (the field depends on 시간,time)
  • time-independent field

Sub:
보존장,conservative_field ( rel 보존계,conservative_system 보존,conservation )

일변수 미적분학은 함수
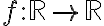$f:\mathbb{R}\to\mathbb{R}$ 만을 다뤘으며,
다변수 미적분학은 이를 확장하여 함수
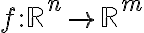$f:\mathbb{R}^n\to\mathbb{R}^m$ 을 다룬다. 특히 두 가지가 중요한데,
스칼라장은 함수
$f:\mathbb{R}^n\to\mathbb{R}$
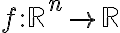
벡터장은 함수
$f:\mathbb{R}^n\to\mathbb{R}^n$
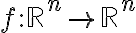
(Essential eng. math. p111)

방향장,direction_field or slope_field 기울기마당 기울기장
기울기,slope를...
이건 미분방정식,differential_equation의 해를 시각화하는 수단인가?
짧은 선분들(short straight-line segments)을 lineal elements라고 함. // 선분,line_segment lineal_element

중력장,gravitational_field
[https]물리학백과: 중력장

보존장 (curr see 보존계,conservative_system 보존,conservation)


장 := 함수: 위치,position → (스칼라 혹은 벡터)
field(position) = (scalar or vector)


Note: 영단어 field의 수학에서의 다른 뜻은 체,field

----