AKA 면적
기호는 보통 A(area에서?), S(surface에서?)가 쓰임.
기호는 보통 A(area에서?), S(surface에서?)가 쓰임.
여러 면적 ¶
단면적 - cross section? section area?
surface_area 표면적 = 겉넓이 = 겉면적 = surface area(곡면넓이) : 3D 도형의 바깥 넓이
{
surface_area 표면적 = 겉넓이 = 겉면적 = surface area(곡면넓이) : 3D 도형의 바깥 넓이
{
bmks en
Paul's Online Notes > Section 8.2 : Surface Area
https://tutorial.math.lamar.edu/Classes/CalcII/SurfaceArea.aspx
{
회전체의 겉넓이.
회전체의 겉넓이를 계산할 때는 원뿔,cone의 절두체,frustum를...
}
Paul's Online Notes > Section 8.2 : Surface Area
https://tutorial.math.lamar.edu/Classes/CalcII/SurfaceArea.aspx
{
회전체의 겉넓이.
회전체의 겉넓이를 계산할 때는 원뿔,cone의 절두체,frustum를...
}
극곡선 회전체 겉 넓이
Area of a Surface of Revolution of a Polar Curve
Area of a Surface of Revolution of a Polar Curve
점
이 곡선을 x나 y 축으로 회전한 입체도형의 넓이 공식은
1. x축 둘레로 회전 )
^2} d\theta)
2. y축 둘레로 회전 )
^2} d\theta)
(Thomas 11e p729)
(easy, del ok)
두 곡선,\,y=g(x)) 그리고 두 직선
그리고 두 직선 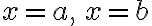 에 둘러싸인(bounded) region의 넓이는
에 둘러싸인(bounded) region의 넓이는
 가 연속이고
가 연속이고 ![$\forall x\in[a,b],\,f(x)\ge g(x)$ $\forall x\in[a,b],\,f(x)\ge g(x)$](/123/cgi-bin/mimetex.cgi?\Large \forall x\in[a,b],\,f(x)\ge g(x)) 일 때
일 때
![$\int_a^b \left[ f(x)-g(x) \right] dx$ $\int_a^b \left[ f(x)-g(x) \right] dx$](/123/cgi-bin/mimetex.cgi?\Large \int_a^b \left[ f(x)-g(x) \right] dx)
두 곡선 ,\,y=g(x)) 및 두 직선
및 두 직선 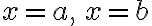 사이 넓이는
사이 넓이는
-g(x) \right| dx)
(Stewart)
두 곡선
관련 ¶
곡면,surface의 성질? 폐곡면,closed_surface, 표면... 평면,plane?
노름,norm, 측도,measure?
도형,figure
면적분,surface_integral, 면적적분 (넓이적분?)
정적분,definite_integral의 결과는 부호,sign가 있는(signed) 면적.
카발리에리_원리,Cavalieri_principle
{ ...부피,volume에도 링크 필요함.
Cavalieri's principle
![[https]](/123/imgs/https.png) 수학백과: 카발리에리의 원리
수학백과: 카발리에리의 원리
 Cavalieri's_principle
Cavalieri's_principle
https://mathworld.wolfram.com/CavalierisPrinciple.html
 카발리에리의_원리
카발리에리의_원리
노름,norm, 측도,measure?
도형,figure
면적분,surface_integral, 면적적분 (넓이적분?)
정적분,definite_integral의 결과는 부호,sign가 있는(signed) 면적.
Simpson's rule
trapezoidal rule etc.
행렬식,determinanttrapezoidal rule etc.
카발리에리_원리,Cavalieri_principle
{ ...부피,volume에도 링크 필요함.
Cavalieri's principle
![[https]](/123/imgs/https.png) 수학백과: 카발리에리의 원리
수학백과: 카발리에리의 원리평면 도형의 넓이 / 공간 도형의 부피 / ... 를 구할 때 사용되는 원리인데..
https://mathworld.wolfram.com/CavalierisPrinciple.html
이것은 푸비니_정리,Fubini_theorem의 particular case이다. (wpen - see also)
....
다음 세 개는 같은거?? CHK
면적소 surface element
면적 미분소 differential area // 미분,differential 넓이,area
미소면적 ds - see 좌표계,coordinate_system#s-11
QQQ 영역,region과 관계?
다음 세 개는 같은거?? CHK
면적소 surface element
면적 미분소 differential area // 미분,differential 넓이,area
미소면적 ds - see 좌표계,coordinate_system#s-11
QQQ 영역,region과 관계?
면적이 분모 ¶
분모가 (대개) 면적인 것들. 이 경우 분모를 보통 '단위면적'으로 칭함.
압력,pressure = 누르는 힘 / 면적
변형력,stress = 물체 내부 힘 / 면적
전류밀도,current_density는 보통 면적 당으로 정의. = 전류 / 면적 (A/m2)
선속밀도,flux_density = 선속,flux / 면적
전속밀도,electric_flux_density = 전속,electric_flux / 면적 (C/m2)
자속밀도,magnetic_flux_density = 자속,magnetic_flux / 면적 (Wb/m2)
밀도,density (중에서 면적밀도)
파동,wave의 세기는 면적 기준??? - 관련: 파면,wavefront
변형력,stress = 물체 내부 힘 / 면적
전류밀도,current_density는 보통 면적 당으로 정의. = 전류 / 면적 (A/m2)
선속밀도,flux_density = 선속,flux / 면적
전속밀도,electric_flux_density = 전속,electric_flux / 면적 (C/m2)
자속밀도,magnetic_flux_density = 자속,magnetic_flux / 면적 (Wb/m2)
밀도,density (중에서 면적밀도)
파동,wave의 세기는 면적 기준??? - 관련: 파면,wavefront

