곡면상의 한 점에서 곡면에 접하는 직선에 수직한 직선.[1]
![[https]](/123/imgs/https.png) 수학백과: 법선
수학백과: 법선
![[https]](/123/imgs/https.png) 물리학백과: 법선
물리학백과: 법선
![[https]](/123/imgs/https.png) 두산백과: 법선
두산백과: 법선
}
{
라틴어 secans(뜻: cutting)에서 유래. 곡선,curve을 자르는(cut)/교차하는(intersect) 그래서 두 번 이상 만나는 직선,line. (Stewart 2.1)
![[https]](/123/imgs/https.png) 수학백과: 법선
수학백과: 법선![[https]](/123/imgs/https.png) 물리학백과: 법선
물리학백과: 법선방향,direction이 둘
"법선 벡터의 경우 2가지 방향인 안쪽 방향(inward-pointing normal vector)과 바깥쪽 방향(outward-pointing normal vector)이 가능"
그래서 관례가....? tbw
"법선 벡터의 경우 2가지 방향인 안쪽 방향(inward-pointing normal vector)과 바깥쪽 방향(outward-pointing normal vector)이 가능"
그래서 관례가....? tbw
![[https]](/123/imgs/https.png) 두산백과: 법선
두산백과: 법선}
{
라틴어 secans(뜻: cutting)에서 유래. 곡선,curve을 자르는(cut)/교차하는(intersect) 그래서 두 번 이상 만나는 직선,line. (Stewart 2.1)
만나는 점이 두 개인 경우 그 사이의 선분,line_segment만 생각하면, 현,chord과 조금 비슷?
}
사선/경사진 점근선 oblique or slant line asymptote
}
점근선,asymptote
{AKA asymptotic line
수직점근선 vertical asymptote { ex. 그래프는 무수히 많은 수직점근선을 가진다. }
그래프는 무수히 많은 수직점근선을 가진다. }
수평점근선 horizontal asymptote
사선점근선 oblique/slant asymptote
수직점근선 vertical asymptote { ex.
수평점근선 horizontal asymptote
사선점근선 oblique/slant asymptote
사선/경사진 점근선 oblique or slant line asymptote
유리함수,rational_function 분자의 차수가 분모의 차수보다 크면 그래프는 사선점근선을 갖는다.
}
The function) will have a horizontal asymptote at
will have a horizontal asymptote at  if either of the following are true.
if either of the following are true.
=L)
=L)
(https://tutorial.math.lamar.edu/Classes/CalcI/LimitsAtInfinityI.aspx)
}
개인적으로 '점근수직선', '점근수평선'이 더 나은 번역 같다.
점근적 asymptotic
{점근적 asymptotic
The function
The line  is called a horizontal asymptote of the curve
is called a horizontal asymptote of the curve ) if either
if either
=L) or
or
=L)
(Stewart 9e p128 Def3)
asymptote는 무한 극한과 관련? chk
trivial: 수평선(horizontal line), 수직선(vertical line), 수직선(number line) - 수직선,number_line, 사선(oblique line) (=slant? slanted? slanting? incline? isocline?) (그리고 diagonal과 oblique의 차이는 뭐지? 서술. tbw. - see  Diagonal
Diagonal  대각선)
대각선)
Compare:직선(straight line) vs 곡선,curve - 방향,direction이 일정한 지 여부
반직선,ray
축,axis
서로 다른 직선이 점,point에서 만나면 각,angle이 생김 직선은 곡률,curvature이 0인 곡선임.
선분,line_segment반직선,ray
축,axis
직선의 기울기,slope를 생각 가능.
직선-직선간, 직선-점 간, 직선-평면간, (또 있으면 여기 추가) 등의 거리,distance를 생각 가능.
1. tmp CLEANUP ¶
{
ex.
3차원 공간에서 직선의 방정식
2차원에서는
주어진 직선과 평행한 벡터인 방향벡터,direction_vector를 생각 가능. see 방향수,direction_number, later 방향,direction.
}
ex.
3차원 공간에서 직선의 방정식
2차원에서는
주어진 직선과 평행한 벡터인 방향벡터,direction_vector를 생각 가능. see 방향수,direction_number, later 방향,direction.
}
직선은 일차방정식(선형방정식,linear_equation)의 해 또는 그래프와 관련.
4. 직선의 polar form ¶
straight line의 극형식,polar_form은 밑의 intercept form에서 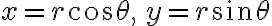 를 넣어서
를 넣어서
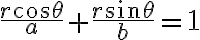
이건 간단히 하면 다음 꼴이 됨 (과정 생략, 그림 필요하고 복잡. 책 참조.)
=d)
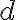 는 원점에서 직선까지의 (최단)거리.
는 원점에서 직선까지의 (최단)거리. 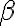 는 원점에서 직선까지 거리를 표시하는 선의 각.
는 원점에서 직선까지 거리를 표시하는 선의 각.
(Heinbockel Vol1 p39)
(Heinbockel Vol1 p39)
5.1. skew lines ¶
from wpsimple: 평행parallel하지도 교차intersecting하지도 않음. 같은 평면,plane에 있을 수 없음. 3차원(이상?)에서만 존재 가능.
 Skew_lines
Skew_lines
 Skew_lines
Skew_lines
 꼬인_위치
꼬인_위치
https://mathworld.wolfram.com/SkewLines.html
https://mathworld.wolfram.com/SkewLines.html
6. Misc: 2D 직선 방정식 여러 꼴의 영어 표현 ¶
고정점 ) 을 지나고 기울기가
을 지나고 기울기가 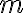 인 직선의 방정식은
인 직선의 방정식은
) (point-slope form of the equation of a line)
(point-slope form of the equation of a line)
y절편이 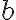 이면 점
이면 점 ) 를 지나므로 위에 대입하면
를 지나므로 위에 대입하면 ) 따라서
따라서
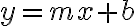 (slope-intercept form)
(slope-intercept form)
수직선(vertical line)등을 포함한 일반적인 꼴은
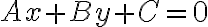 (A and B not both 0) (general linear equation)
(A and B not both 0) (general linear equation)
(Varberg)
point-slope equation of the line
)
slope-intercept equation of the line
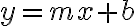
general linear equation (A and B not both 0)
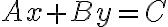
(Thomas)
general equation
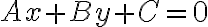
slope-intercept form
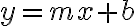
intercept form - y축을 (0,b)에서, x축을 (a,0)에서 만날 경우 (절편)
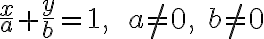
(Heinbockel Vol 1 p38)

