= 벡터장의 발산?
델,del,나블라,nabla와 내적,inner_product을 했으므로 결과가 항상 scalar?
내적은 아니라 or 내적과는 유사하긴 하지만 다르다 하는데. CHK
벡터장,vector_field의 발산 결과는 스칼라장,scalar_field임.벡터장 F 에 대해 div F를 발산함수라 한다는데(수학백과) 이것도 divergence function 찾아보면 굳이 외국에선 이름지어 부르지 않는 듯 한데... (delme)
장의 원천점에서 양이고 싱크점(sink)에서 음, 그 외에서는 0? (Sadiku)
3차원 cartesian의 예를 들면, 벡터장 =F_x(x,y,z)\hat{x}+F_y(x,y,z)\hat{y}+F_z(x,y,z)\hat{z}) 이면
이면
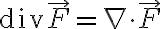
\cdot(F_x,F_y,F_z))
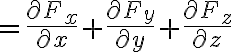
i.e.
cyli
sphe TBW
∇·v>0 : divergence : field가 밖으로 뻗어 나감
∇·v<0 : convergence : field가 안으로 모여듦
∇·v<0 : convergence : field가 안으로 모여듦
1. Zill ¶
벡터장,vector_field 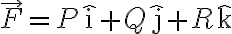 의 발산(divergence)은 스칼라함수,scalar_function
의 발산(divergence)은 스칼라함수,scalar_function
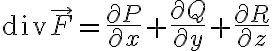
이다. 델 연산자(델,del,나블라,nabla)를 사용하면
+\frac{\partial}{\partial y}Q(x,y,z)+\frac{\partial}{\partial z}R(x,y,z))
로 나타낼 수 있다.
(Zill 6e ko 정의 9.7.2 p638)
3. Sadiku 3.6 ¶
폐곡면 S로부터 밖으로 유출되는 벡터장  의 순 선속은 적분
의 순 선속은 적분 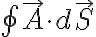 를 이용하여 구할 수 있다. (see 선적분,line_integral의 Sadiku 3.3)
를 이용하여 구할 수 있다. (see 선적분,line_integral의 Sadiku 3.3)  의 발산은 폐증분면(closed xxxx surface?)에 대한 단위체적당 밖으로 유출되는 선속,flux으로 정의된다.
의 발산은 폐증분면(closed xxxx surface?)에 대한 단위체적당 밖으로 유출되는 선속,flux으로 정의된다.
점 P에서  의 발산은 체적이 점 P 근처로 줄어들 때 단위체적당 밖으로 유출되는 선속이다.
의 발산은 체적이 점 P 근처로 줄어들 때 단위체적당 밖으로 유출되는 선속이다.
그러므로
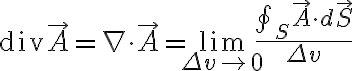
여기서
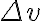 : P가 위치한 폐곡면 S에 의해 둘러싸인 체적
: P가 위치한 폐곡면 S에 의해 둘러싸인 체적
물리적 의미: 주어진 점에서 벡터장  의 발산은 그 점에서 장이 얼마나 많이 발산하거나 퍼지는지를 뜻함
의 발산은 그 점에서 장이 얼마나 많이 발산하거나 퍼지는지를 뜻함
직각좌표계에서
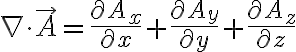
원통좌표계에서
+\frac{1}{\rho}\frac{\partial A_{\phi}}{\partial \phi}+\frac{\partial A_z}{\partial z})
구좌표계에서
+\frac{1}{r\sin\theta}\frac{\partial}{\partial\theta}(A_{\theta} \sin\theta)+\frac{1}{r\sin\theta}\frac{\partial A_{\phi}}{\partial\phi})
특성 생략
발산정리 생략
발산정리 생략
4. 정길수 ¶
벡터  가
가 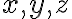 축 방향성분으로 각각
축 방향성분으로 각각 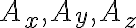 를 갖는다면
를 갖는다면
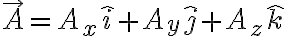
로 쓸 수 있다. 이 벡터가 전 공간으로 발산할 때 x축으로 변화한 비율은 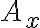 가 x에 대해 변화한 것이므로
가 x에 대해 변화한 것이므로
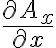
로 쓸 수 있다. 즉 변화한 비율이라는 것은 도함수
-A_x(x)}{\Delta x}=\frac{dA_x(x)}{dx})
를 뜻하므로 다변수 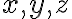 에 대해서는 편미분을 이용하여 x축 변화율
에 대해서는 편미분을 이용하여 x축 변화율 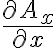 로 쓸 수 있다. 마찬가지로 y축으로 발산하여 변화한 비율은
로 쓸 수 있다. 마찬가지로 y축으로 발산하여 변화한 비율은 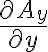 이고 z축에 대한 변화 비율은
이고 z축에 대한 변화 비율은  이다.
이다.
그러므로 체적 ) 에 대해
에 대해  가
가
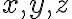 방향으로 발산한 벡터
방향으로 발산한 벡터  의 총발산량은 각 방향으로의 발산량을 합한 것과 같으므로
의 총발산량은 각 방향으로의 발산량을 합한 것과 같으므로
\Delta v)
여기서  로 놓으면
로 놓으면
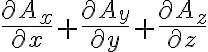
\cdot(A_x\hat{i}+A_y\hat{j}+A_z\hat{k}))
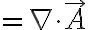
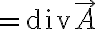
이것을 발산이라 하고  은 단위체적을 뜻하므로 단위체적에서 발산하는 것(전기력선 수, 유체의 유출량 등)을 뜻한다.
은 단위체적을 뜻하므로 단위체적에서 발산하는 것(전기력선 수, 유체의 유출량 등)을 뜻한다.
x축으로 발산한 발산량(변화량)은  이고,
이고,
y축으로 발산한 발산량은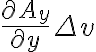 이고,
이고,
z축으로 발산한 발산량은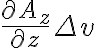 이다.
이다.
그러므로 y축으로 발산한 발산량은
z축으로 발산한 발산량은
5.1. 좌표계 별 발산 ¶
직각
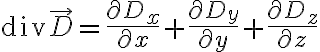
원통
 + \frac{\partial D_{\phi}}{\rho \partial \phi} + \frac{\partial D_z}{\partial z}) 왜 이렇게 rho를 썼다가 cancel하는지 잘 이해 못함 CHK
왜 이렇게 rho를 썼다가 cancel하는지 잘 이해 못함 CHK
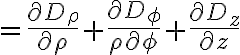
구면
 + \frac{\partial}{r\sin\theta\partial\theta}(\sin\theta D_{\theta}) + \frac{\partial D_{\phi}}{r\sin\theta \partial \phi})
// 발산정리,divergence_theorem (4강 38m)
가우스_법칙,Gauss_s_law#s-9에서 양변을 체적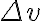 로 나누면
로 나누면
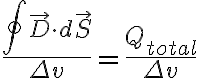
극한 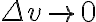 를 취하면, 위 발산의 정의에 의해
를 취하면, 위 발산의 정의에 의해
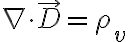
또...
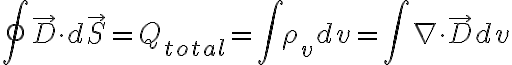
따라서
DELME 예제
{
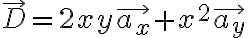 이면
이면
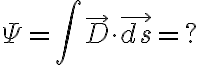
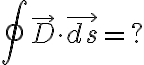
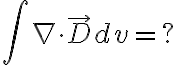
x는 0~1,![$(x\in[0,1])$ $(x\in[0,1])$](/123/cgi-bin/mimetex.cgi?\Large (x\in[0,1])) y는 0~2, z는 0~3
y는 0~2, z는 0~3
즉 직접 확인해봐라는 문제.
참고로 이 문제는 체적적분이 면적분보다 쉽다.
가우스_법칙,Gauss_s_law#s-9에서 양변을 체적
DELME 예제
{
x는 0~1,
즉 직접 확인해봐라는 문제.
참고로 이 문제는 체적적분이 면적분보다 쉽다.
Sol.
6. 성질 ¶
벡터장의 발산 연산(divergence operation)은
분배법칙,distributivity이 성립함.
교환법칙,commutativity과 결합법칙,associativity은 성립 안함.
분배법칙,distributivity이 성립함.
교환법칙,commutativity과 결합법칙,associativity은 성립 안함.
7. Links ko ¶
3차원 데카르트 좌표계에서 벡터 함수의 다이벌전스(발산)
https://freshrimpsushi.github.io/posts/divergence-of-fector-function-in-cartesian-cooridenates-system/
https://freshrimpsushi.github.io/posts/divergence-of-fector-function-in-cartesian-cooridenates-system/
곡선 좌표계에서 벡터 함수의 다이벌전스
https://freshrimpsushi.github.io/posts/divergence-of-a-vector-function-in-a-cuvilinear-coordinate-system/
https://freshrimpsushi.github.io/posts/divergence-of-a-vector-function-in-a-cuvilinear-coordinate-system/
발산은
페이지를 분리해야 한다면 어떻게 해야 하는가.. 벡터장의 발산 vs 수열의 발산?
2022-10-10 벡터장의 발산은 여기에 두고, 수열/함수의 발산은 발산성,divergence로 할까?
- 급수,series, 수열,sequence등이 수렴하지 않는 것, 즉 수렴의 반대말 (QQQ 이건 (+∞ -∞ 진동) 세가지 뿐인가?)
- 벡터미적분,vector_calculus에서 벡터가 밖으로 뻗어 나가는 ..
페이지를 분리해야 한다면 어떻게 해야 하는가.. 벡터장의 발산 vs 수열의 발산?
2022-10-10 벡터장의 발산은 여기에 두고, 수열/함수의 발산은 발산성,divergence로 할까?
암튼 수열/함수의 발산에 대해 임시로 적어보면
{
{
함수의 발산
이건 극한_EpsilonDeltaLimitDefinition에 합칠까..
암튼 이것의 정의는 극한,limit의 엄밀한 정의 그쪽 얘기
MKLINK
함수,function
이건 극한_EpsilonDeltaLimitDefinition에 합칠까..
암튼 이것의 정의는 극한,limit의 엄밀한 정의 그쪽 얘기
MKLINK
함수,function
수열의 발산
The notation
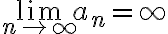
means that for every positive number 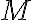 there is an integer
there is an integer 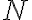 such that
such that
MKLINK
수열,sequence
Opp. : 수열의 수렴 - curr at 수렴,convergence#s-5
The notation
if 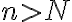 then
then 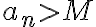
(Stewart)MKLINK
수열,sequence
Opp. : 수열의 수렴 - curr at 수렴,convergence#s-5
}
그리고 Kullback-Leibler_divergence(KLD) Jensen-Shannon_divergence(JSD)는 여기의 sub로 할지 아니면 따로 분리한 어떤 page의 sub로 할지 TBD.
여기에 그냥 한 section으로 하는게 최선인가?
암튼 항상 발산으로 번역되는 divergence의 뜻은 일단 지금까지 세 분야에서 보임- sequence
- vector calculus
- prob/stat/entropy - KLD, JSD
Twins:
https://ghebook.blogspot.com/2010/07/divergence.html
![[https]](/123/imgs/https.png) 수학백과: 벡터장의 발산
수학백과: 벡터장의 발산
https://www.khanacademy.org/math/multivariable-calculus/multivariable-derivatives/divergence-and-curl-articles/a/divergence
 Divergence
Divergence
 발산_(벡터)
발산_(벡터)
https://ncatlab.org/nlab/show/divergence
https://ghebook.blogspot.com/2010/07/divergence.html
![[https]](/123/imgs/https.png) 수학백과: 벡터장의 발산
수학백과: 벡터장의 발산https://www.khanacademy.org/math/multivariable-calculus/multivariable-derivatives/divergence-and-curl-articles/a/divergence
https://ncatlab.org/nlab/show/divergence


![[http]](/123/imgs/http.png)